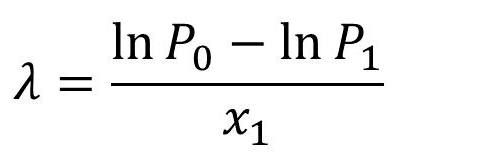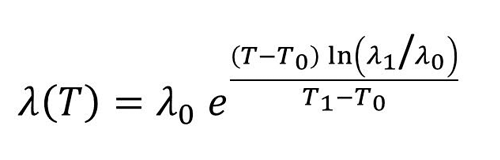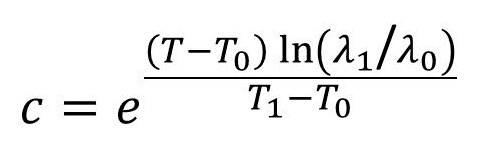ゴム本来の性質から、実はタイヤの空気圧が減少する早さは、温度が高いほど早くなり、温度が低いほど遅くなるという性質があります。そこで、温度が変わると実際にどのくらい変わりうるのかを計算してみました。その結果は…?
付録として、自分が使用しているタイヤの場合ではどうなるのか簡単に調べる方法についても紹介します。
はじめに:この記事が説明していること

前回の記事で、タイヤの空気圧が指数関数的に減少することは分かった。で、実走ではどうなるの?

ゴムの性質上、温度が高いほど空気圧の減少が早くなるので、特に7月や8月の真夏日は、他の季節よりも空気圧の減少が早くなるでしょう。ただし影響が出るとすればラテックスの場合で、ブチルはもともと空気圧の減少がものすごく遅いので、実用上はほとんど影響ないでしょう。

ラテックスの場合は具体的にはどの程度早くなるの?

条件にもよりますので一概には言えませんが、例えば過ごしやすい室内で「空気を7bar入れてから2日経つと5barに減少するタイヤ」が、真夏日に実走で使うと「1日半程度で5barになる」くらいには変わるかもしれません。

自分の使用しているタイヤチューブの漏れ速度を知りたいんだけど、簡単に調べる方法はない?

簡易的な方法として、初日に7 barにセットして翌々日に空気圧を測定するだけで面倒な計算をしなくても誰でも漏れ速度が分かる方法を紹介しますので、ぜひ試してみて下さい。
タイヤの空気圧減少の法則のおさらい
前回の記事では、マスター氏の行ったラテックス(Vittoria Latex)とブチル(Panaracer R’Air)の空気圧の時間変化を調べた実験結果の解析を通して、
- ゴム本来の性質により、タイヤの空気圧は時間とともに指数関数的に減少する(※タイヤの内容積が変わらない場合)。
- タイヤの空気圧が減少するスピードは「漏れ速度」というパラメータで表せる(※筆者による独自の用語です)。
- 漏れ速度が分かれば、簡単な予測式で空気圧の減少をある程度は予想できる。
…といったことなどを紹介しました。
正直に申し上げると、前回はマスター氏の実験結果の解析結果と、その結果から分かるタイヤの空気圧減少の法則を理数系に明るくない方にもなるべく分かりやすく伝えることを主眼としたため、「で、実走ではどうなの?」といった問いに対してはあまり役に立つ知見は提供できず、その点では行き届かない点がありました。
また、実験の期間が1週間という長い期間と根気を要するため、そのまま行うにはかなりハードルが高いものでした。
そこで本稿では「実走ではどうなのか」「漏れ速度を誰でも簡単に調べる方法はないか」という2点について、ほんの少しかもしれませんが、実用面でも参考になりそうな話題を提供できればと思います。
暑い日はタイヤの空気圧の減少がどのくらい早くなる?
シミュレーション結果
さて、冒頭でも申し上げた通り、ゴム本来の性質として、タイヤのチューブは温度が高いほど空気が漏れるのが早くなり、温度が低いほど遅くなるという性質があります。本編では、この性質が実走にどの程度影響してくるかを考えてみたいと思います。
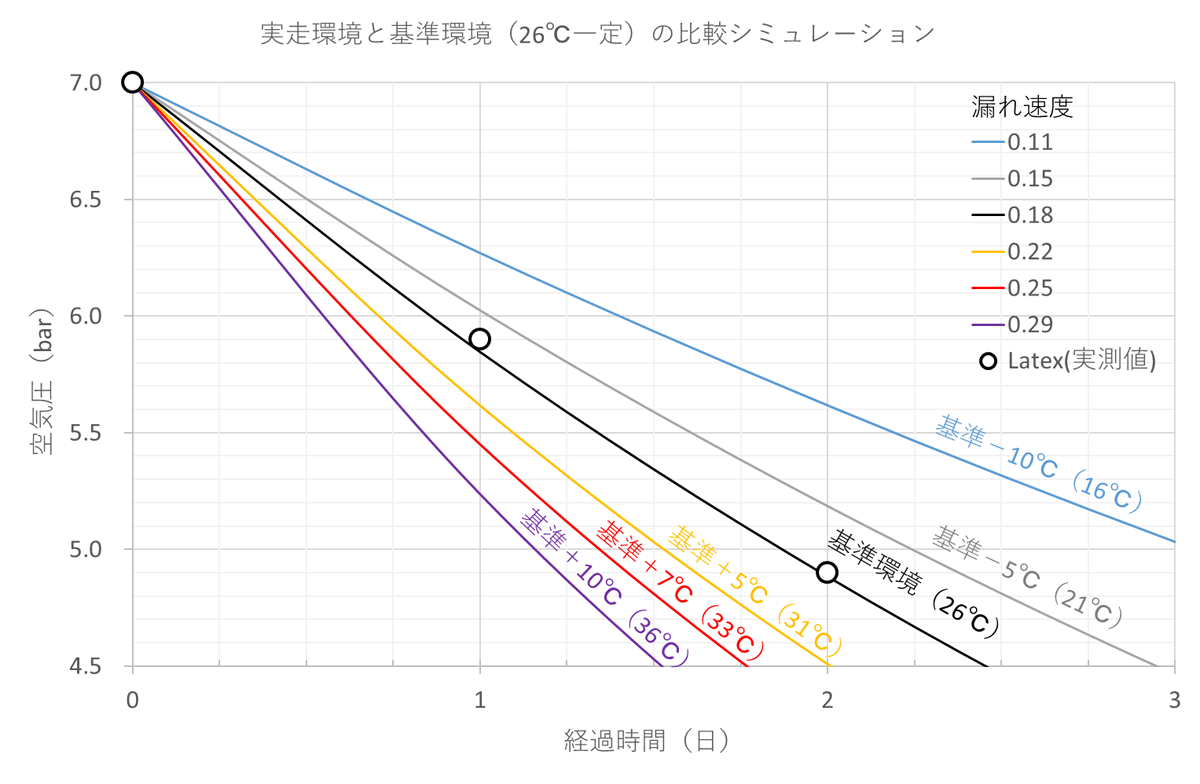
下の図はマスター氏のラテックスの実験データを元に、実験で使用したのと同じタイヤを異なる温度環境で使用したら空気圧の減り方がどう変わるか、をシミュレーションしてみた結果をグラフにしたものです。
初期圧力を7 barとしてスタートして、種々の温度での空気圧の変化を3日目までシミュレーションしています。どの程度温度が変わるとどの程度早くなったり遅くなったりするのか、なんとなく、でも感じ取っていただければと思います。
図の見かたですが、まず黒丸がマスター氏の実測値、黒い線は実測値を理論式で内挿した曲線です。マスター氏にお尋ねしたところ、実験はなるべく26℃に保たれた環境で行ったそうですから、これを基準環境とします(個人が自宅でやれる実験としては十分最善を尽くされただろうと思いますので、ここでは平均温度が26℃だったものとして先へ進みます)。
黄色、赤色、紫の線はそれぞれ基準環境より温度が5℃、7℃、10℃高い場合の計算結果で、温度が高いほど空気圧の減少が早くなります。灰色と水色は反対にそれぞれ基準環境より温度が5℃、10℃低い場合で、こちらは温度が下がるほど遅くなります。
結果は視覚的にはごらんの通りですが、もう少し具体的に、一例として「7 barから5 barに減少するまでの所要時間」で比較してみましょう。
この場合、所要時間と温度の関係は下の表のようになります。気温ではなく、タイヤの温度であることに注意してください。
| タイヤの温度(℃) | 基準環境との温度差(℃) | 7 barから5barに減少するまでの所要時間 | 基準環境との所要時間の差 |
|---|---|---|---|
| 16 | -10 | 75 | +31 |
| 21 | -5 | 56 | +12 |
| 26 | ±0 | 44 | ±0 |
| 31 | +5 | 37 | -7 |
| 33 | +7 | 32 | -12 |
| 36 | +10 | 28 | -16 |
この表から、例えば基準環境から7℃高い場合、すなわち33℃の場合では、再補充が必要になるまでの所要時間がちょうど半日(12時間)短くなる、ということなどが分かります。
元が指数関数なので当然と言えば当然なのですが、やはり実際に計算してみないと分からない、直感では予想しにくい現象ですね。なおこの表の計算方法は、付録で説明しています。
シミュレーション結果のまとめ
以上から、基本的にはマスター氏の使用タイヤと同程度の漏れ速度ならば、
- 温度の影響があったとしても、日帰りライドでは大きな影響はない。
- タイヤの温度が33℃以上になるような日にロングライドを行う場合には、空気を再補充すべきタイミングが普段よりも半日かそれ以上早くなるかもしれない。
といったことが言えそうです。もちろんラテックスの場合です。
さて、数時間の違い程度なら体感的には誤差かもしれませんが、半日の違い、というのはそろそろ誤差と片付けられなくなってくるラインかもしれません。
そこで、次は「タイヤの温度が33℃以上になる日ってどんな日?」という点について考えてみます。
真夏日のタイヤの温度を考える
気温と路面温度の関係
実走時のタイヤの温度を考える上で、最も影響が大きいのはやはり気温と路面温度でしょう。ちょうど気温と路面温度がほぼリンクしているという文献があったので、まずはそれを元に考えてみます。
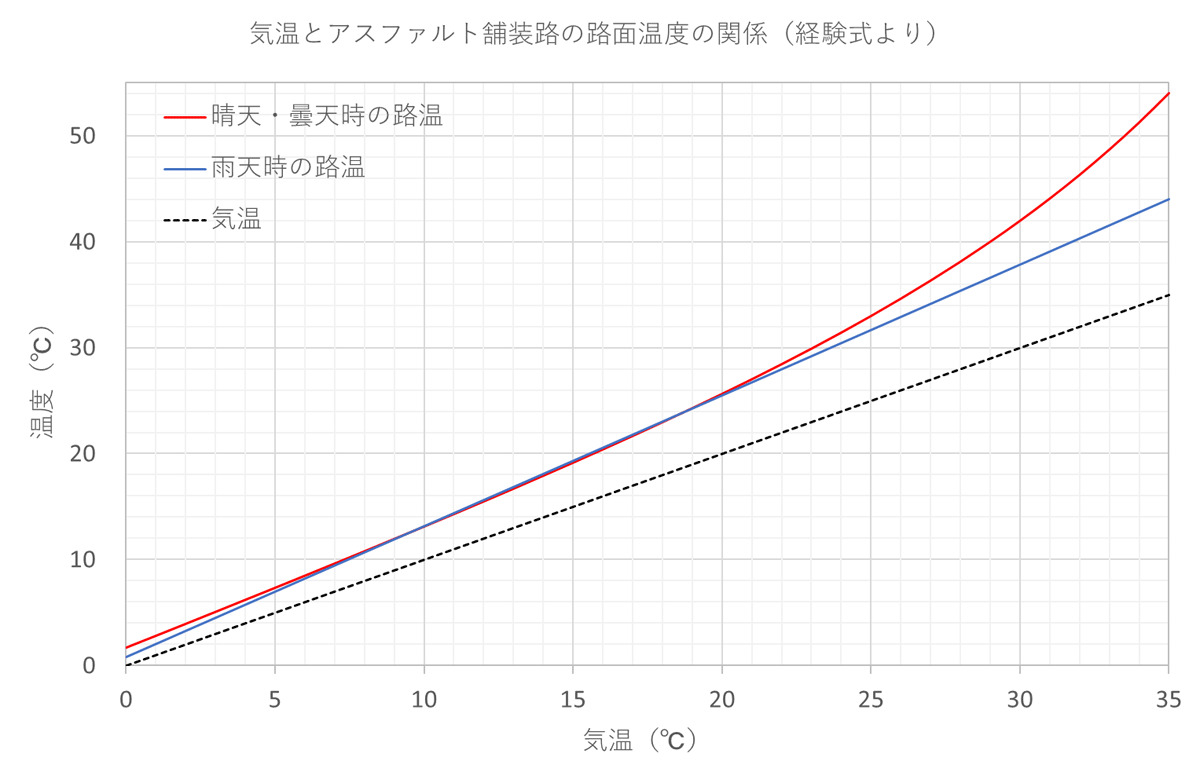
下の図は気温とアスファルト舗装路の路面温度の関係の経験式をグラフにしたものです。
見ての通り、この経験式では晴天時と曇天時は同じ扱いになっているのが興味深いところです。確かに曇天でも気温が高い日は雲越しからでも熱線が降り注いでいる感じはしますが、要するに同じ30℃なら、雲があろうがなかろうが30℃は30℃、ということでしょうか。
とまれ、とりあえず晴天・曇天の暑い日に参考になりそうな情報を探してみることにすると、ひとまず気温28℃の時の路面温度は気温より10℃高く、気温が高くなるほど気温と路面温度の差は大きくなる、といったことが読み取れます。
この経験式の元になったデータの成り立ちから考えて、この経験式は、時間帯に関係なく晴天・曇天であれば気温が28℃の時の路面温度の平均値は38℃程度、という見かたで見ればよいのだろうと思います。
実用上、ロングライドにおいては一日の平均気温を拠り所とするしかないので、その点ではこの資料は今回の検討にぴったりです。
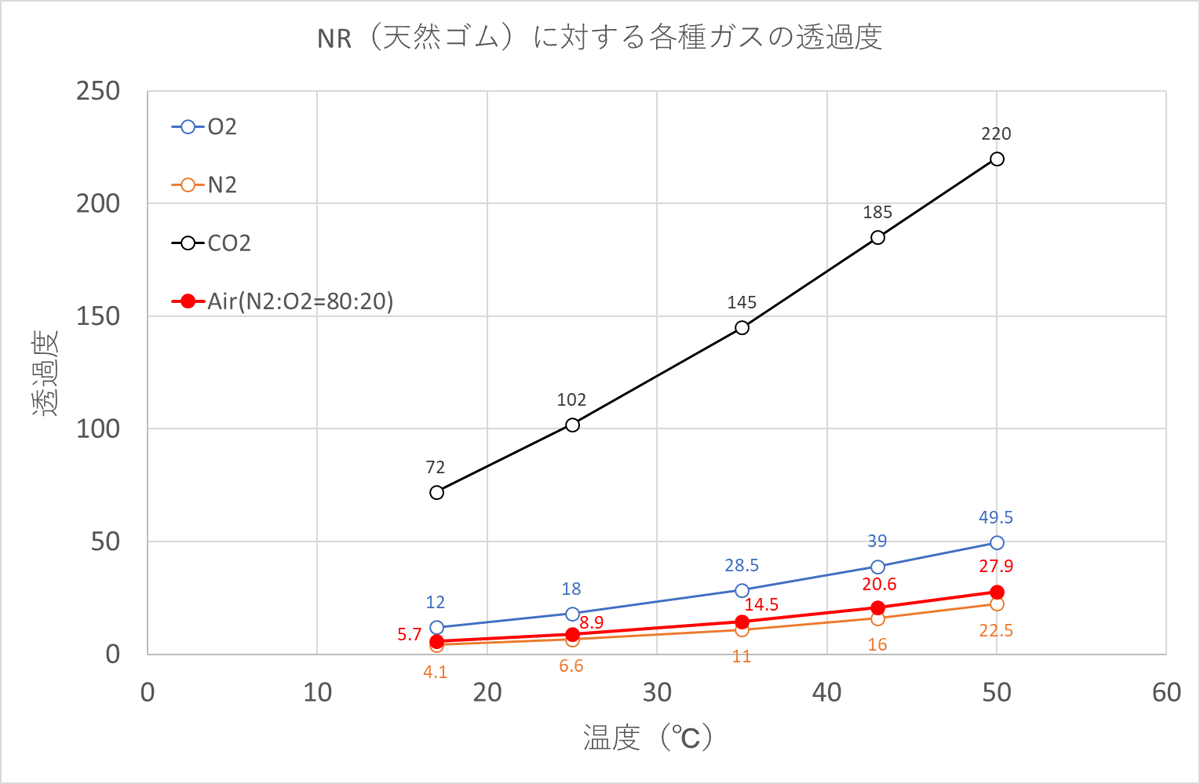
さて、平均気温28℃というのは、その年の傾向にもよるでしょうが、東京で言えばだいたい7月・8月頃の気候に相当します。参考までに、昨年の東京の月別平均気温・最高気温と最低気温の平均を下の図に示します。これから、最高気温が30℃を超えるような真夏日でも、平均気温で見るとだいたい28℃くらいだろう、ということが分かります。
したがって、地方にもよるでしょうが、7月・8月頃の晴天・曇天時で平均気温28℃の日の路面温度は平均ではだいたい38℃、ということまでは言えそうです。
気象庁ホームページのデータを元に作製
平均気温28℃の日のタイヤの平均温度を考える
では1日の平均気温が28℃、平均路面温度が38℃のときのタイヤの温度は何℃でしょうか?
実測するか熱力学的なシミュレーションなどできればいいのですが、どちらもきちんとやろうとすると大変なので、ここはアバウトに、気温と路面温度のちょうど中間の33℃くらいだろう、と考えることにします。
同様に考えると、今回のシミュレーションで基準環境とした(タイヤの平均温度が)26℃に対応する日は「平均気温がだいたい22℃くらいの晴天・曇天の日」と見当をつけることができます。これは東京で言えば6月や9月の気候に相当します。
したがって、先ほどのシミュレーション結果と照らし合わせてざっくりとまとめると、マスター氏が実験で使用したタイヤ(ラテックス)の場合、「7月・8月の最高気温が30℃を超えるような真夏日は、6月や9月に比べて空気を再補充すべきタイミングが半日かそれ以上早くなるかもしれない」ということが言えそうです。
また、夏季は地面からの輻射熱で、路面近くの空気の温度は予報の気温よりかなり高いことは実感としてご存知の方も多いと思います。とまれ、1℃や2℃の違いは気にしても仕方がないですから5℃刻みで考えて、選択肢を気温と同じ28℃か、路面温度と同じ38℃か、それとも中間の33℃か、の三択問題で考えると33℃が一番有力、ですよね?
休憩中はノーカウント?
「平均気温28℃の日のタイヤの温度が平均33℃とみなせることは分かった。でも休憩中はノーカンでしょ?その分はさっきの計算よりもズレるのでは?」という疑問は当然出てきそうです。
これは休憩のしかたにもよるでしょう。いわゆる大休憩(仮眠やそこそこ長い時間の休憩)ならもちろんノーカン扱いでよいと思いますが、コンビニ休憩程度ならあまり差はないのではないか、と思います。
ただし、コンビニ休憩でも、休憩時にバイクを日なたに置いておくと、日射や地面からの輻射熱の影響で走行中よりもむしろ(バイク全体が)熱くなるケースがありえます。逆に、夜の場合はもともと昼間よりも気温と路面温度の差が小さくなっているので、休憩中にタイヤが冷えたとしてもやはり影響は小さいでしょう。
本編のまとめ
かなり荒っぽい考察でしたが、
- ゴム本来の性質により、暑ければ暑いほど空気圧の減少は早くなる
- マスター氏が実験で使用したタイヤ(ラテックス)をサンプルとしてシミュレーションすると、7月・8月の最高気温が30℃を超えるような真夏日は、6月や9月に比べて空気を再補充すべきタイミングが半日程度早くなる(ただし長い休憩を除く)
ということを説明しました。
言われるまでもないことかもしれませんが、経験豊富な方ならば、タイヤゲージを使わなくても、おそらくタイヤを指で押しただけでヤバいかどうか程度は判断できるのではないかと思います。
もし指で押さえてヤバそうだったら空気を補充すればいいし、大丈夫そうならまだ補充しなくていい。結局はそれだけのことだと思いますが、本稿が暑い日のタイヤチェックのタイミングの参考になれば幸いです。
付録
以降では
- 漏れ速度を自分でも調べてみたいという酔狂な方に送る、おすすめの超簡単な実験方法
- 漏れ速度の計算や、本編で行った計算に必要な数式の道具箱的なもの
- 本編で話の流れ上説明を省いた内容の補足説明
について述べます。数式といっても内容的には指数関数の基本が分かれば誰でも導出できる程度のものですが、スマホの関数電卓アプリ等を利用すれば手軽に計算が可能なので、興味のある方の参考になれば幸いです。
漏れ速度を簡単に調べるおすすめの方法
必要なものは以下の通りです。
- タイヤゲージ
- なるべく一定温度の環境(基準環境)
- その他、タイヤ、チューブ、ポンプなど書くまでもないもの
何はともあれタイヤゲージは必要です。パナソニックのアナログ式のゲージ、およびデジタル式のゲージに関しては、マスター氏が下の記事で詳しく紹介して下さっています。

やり方は基本的にはマスター氏が最初に行った実験と似ていますが、今回紹介する方法は
- 期間を最大2日間に限定
- 測定は最初と最後の2回だけ
と、これ以上ないほど大幅に簡略化したものです。
手順としては以下の通りです。
- 初期圧力として7 barを充填する
- なるべく一定温度の環境に安置する(できない場合は、平均温度を調べる)
- 2日後(48時間後)に圧力(P)を調べる
- 下の漏れ速度早見表から、漏れ速度を探す
以上です。例えば2日目の圧力が5.0 barだったなら、漏れ速度は表から0.17と分かります。これで、漏れ速度を調べるだけなら電卓さえ不要になりました!
表:漏れ速度早見表
| 経過時間(日) | ||
|---|---|---|
| 圧力(P) | 1 | 2 |
| 7.0 | 0.00 | 0.00 |
| 6.9 | 0.01 | 0.01 |
| 6.8 | 0.03 | 0.01 |
| 6.7 | 0.04 | 0.02 |
| 6.6 | 0.06 | 0.03 |
| 6.5 | 0.07 | 0.04 |
| 6.4 | 0.09 | 0.04 |
| 6.3 | 0.11 | 0.05 |
| 6.2 | 0.12 | 0.06 |
| 6.1 | 0.14 | 0.07 |
| 6.0 | 0.15 | 0.08 |
| 5.9 | 0.17 | 0.09 |
| 5.8 | 0.19 | 0.09 |
| 5.7 | 0.21 | 0.10 |
| 5.6 | 0.22 | 0.11 |
| 5.5 | 0.24 | 0.12 |
| 5.4 | 0.26 | 0.13 |
| 5.3 | 0.28 | 0.14 |
| 5.2 | 0.30 | 0.15 |
| 5.1 | 0.32 | 0.16 |
| 5.0 | 0.34 | 0.17 |
| 4.9 | 0.36 | 0.18 |
| 4.8 | 0.38 | 0.19 |
| 4.7 | 0.40 | 0.20 |
| 4.6 | 0.42 | 0.21 |
| 4.5 | 0.44 | 0.22 |
| 4.4 | 0.46 | 0.23 |
| 4.3 | 0.49 | 0.24 |
| 4.2 | 0.51 | 0.26 |
| 4.1 | 0.53 | 0.27 |
| 4.0 | 0.56 | 0.28 |
漏れ速度を調べる実験の注意点
- 温度はなるべく一定が望ましいです。タイヤは窓からなるべく離して、日光などが直接当たらないように注意して下さい。
- 室内環境がエアコンのリモコンの設定温度通りの温度になっているとは限らないので、気温計があれば利用しましょう。電波時計などに気温の表示機能が付属しているものがありますが、そういったものでも十分でしょう。
- 調べた漏れ速度の値は、必ず平均温度とペアで記録しましょう。
- 精度の観点から基本的に2日目の測定をお勧めしますが、1日目で5bar付近かそれ以下になるような抜けの早いチューブの場合は、1日目で測定してもいいでしょう。早見表にはいちおう1日目で測定した場合の漏れ速度の値も載せています。
- 2点以上の異なる温度(6℃と26℃等、なるべく離れた温度)で漏れ速度を調べると、任意の温度の漏れ速度の予測値を計算できるようになります(計算方法は後述)。
- 実際の作業での注意点などはマスター氏が下の記事で詳しく説明して下さっているので、こちらも参考になると思います。

初期圧力が7 barと7.5 bar、あるいは7 barと8 barの組み合わせで見かけの漏れ速度の値にどの程度の影響があるかは(実際のデータが無いので)執筆時点では何とも言えませんが、理想的には自分の常用する圧力を初期圧力として実験するのがベターでしょう。
タイヤケーシング部分の伸縮の影響について
前回の記事をご覧になっていてお気づきになった方がいらっしゃるかもしれませんが、実は前回の記事では一週間分の測定データの解析結果を元にラテックスの漏れ速度を0.22としていましたが、本稿の本編部分では基準環境の漏れ速度を0.18として計算しました。これは、上述の簡単な実験方法と条件をそろえるためです。つまり、2日目までのデータを元に解析すると0.18だった、というわけです。
この両者の値の差はただのバラつきではなく、タイヤのケーシング部分の伸縮の影響が現れているのではないかと筆者は考えています(他にもそう考えるに足るエビデンスはありますが、本論とは関係ないので本稿では割愛させていただきます)。
タイヤとチューブの構造を考えると、高圧であればあるほど、空気がわずかに漏れても、伸びていたケーシング部分が縮むことにより内容積自体が小さくなろうとする(=圧力を上げようとする)作用がはたらいて、結果的に、単純な指数関数の減圧の法則よりも圧力の減少がゆるやかになるはずです。
一方で、圧力がある程度下がると、ケーシングが縮む余地がなくなって内容積がほとんど変化しなくなり、圧力の減少は単純な指数関数の法則に収束していくはずです。
それゆえ、測定期間が短く測定した圧力レンジが高いほど、見かけ上の漏れ速度の値は素材としての本来の値よりも小さめに出るだろう、ということは容易に予想できます。
このケーシングの伸縮の影響を解析や理論式に組み込むのは非常に面倒なわりに考慮してもおそらく全く得しないので、解析では引き続き無視することにします。実験条件の初期圧力と測定期間を全て同一条件で行うようにすれば実用上は問題ないだろうと思いますが、実験条件が異なる結果同士を比較する場合には注意しなければならない問題かもしれません。
漏れ速度と圧力減少の予測式のおさらい
タイヤの内容積が一定とみなせるとき、漏れ速度をλとすると、空気圧P0(bar)を入れてからx日後の圧力P(x)は、理想的には以下の理論式に従うと考えることができます。本稿ではこの式をタイヤ空気圧の圧力減少の予測式として用います。
P(x)=P0e-λx
漏れ速度についてのおさらい
漏れ速度は、直感的には「空気圧が一日あたり何%減少する勢いで減少するか」を、100%を1として表した値です(瞬間的な勢いなので、一日単位のマクロな減少率と厳密にはイコールにはなりませんが)。
空気圧の減少が理論式通りにふるまうなら、この漏れ速度が分かっていれば、上の予測式を利用して空気圧の時間変化を予測できることになります。
ただし、漏れ速度はチューブの厚みに反比例します。したがって、同じ銘柄でも組み合わせるタイヤサイズ等の使用状況で変わりうる値である、ということに注意する必要があります。
漏れ速度の簡易的な計算方法
タイヤ空気圧の圧力減少が理論式通りにふるまうとすると、初期圧力P0(bar)を入れてからx1日後の圧力がP1(bar)だったとき、漏れ速度λは以下の式で求めることができます。
任意の温度における漏れ速度と温度補正係数の簡単な求め方
漏れ速度の温度依存性に関して詳しくは後で述べますが、ゴムの空気透過性(漏れ速度)は原則として温度とともに指数関数的に増加する性質があります。
漏れ速度の温度依存性が単純な指数関数で表せるならば、異なる2点の温度(例えば6℃と26℃)で漏れ速度を測定してやることで、簡易的に、任意の温度の漏れ速度を求めることができます。
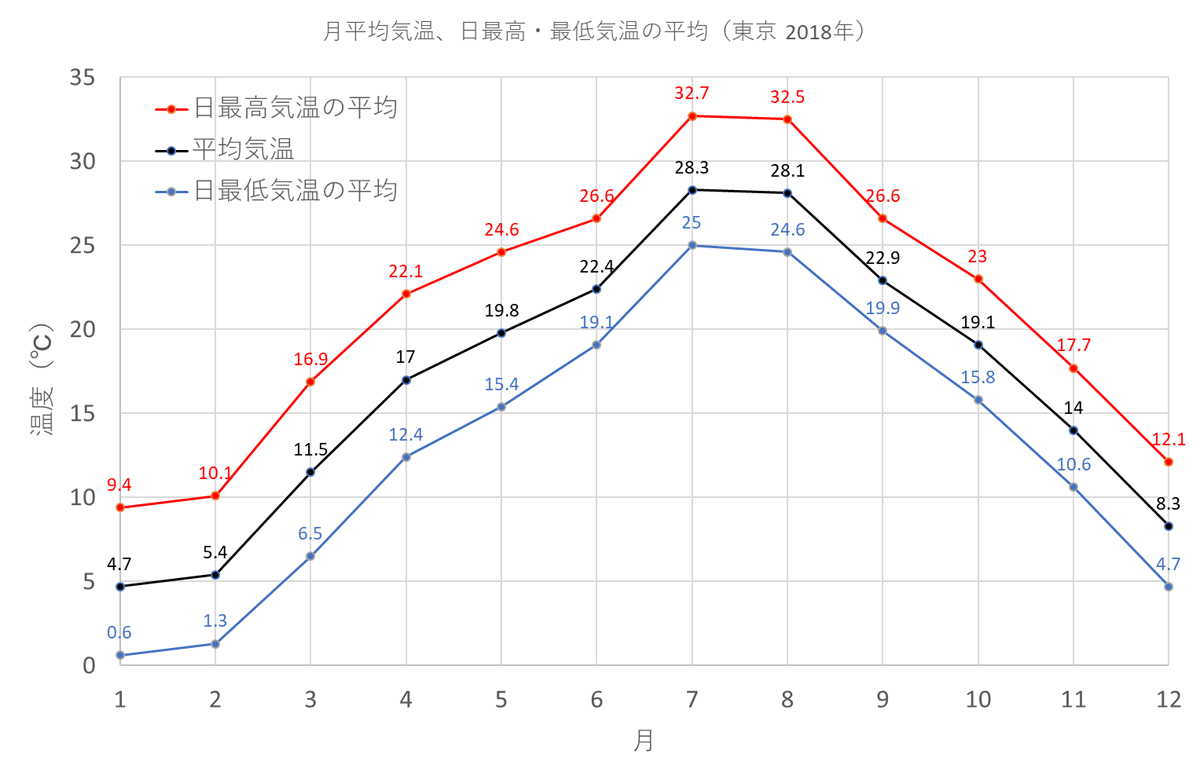
具体的には、簡単な計算により、温度T0(°C)での漏れ速度がλ0、温度T1(°C)での漏れ速度がλ1であった時、温度T(°C)の漏れ速度λ(T)は、温度T0(°C)を基準環境とすると
で表せます。
ここで指数の項をcとおいてみます。
このcを温度補正係数と(勝手に)呼ぶことにすると、任意の温度の漏れ速度は、基準環境の漏れ速度λ0と温度補正係数c(これもTの関数)の積の形で簡単に表すことができます。
λ(T)=λ0 c(T)
漏れ速度は使用状況(組み合わせるタイヤサイズ等との組み合わせ)で変わりうる値ですが、温度補正係数は同じ銘柄(材料)であれば使用状況に関わらず原理的には共通の値になるはずですから、興味のある方は調べてみると一興かと思います。
空気を入れてから任意の圧力に下がるまでの所要時間の計算方法
圧力減少が理論式通りにふるまうとすると、漏れ速度がλの時、初期圧力P0(bar)を入れてからP1(bar)に減少するまでの所要時間x1(日)は以下の式で求めることができます。
x1を24倍すれば、単位を時間に変換できます。
冒頭でたとえ話として記述した「過ごしやすい室内で『空気を7bar入れてから2日経つと5barに減少するタイヤ』が、真夏日に実走で使うと『1日半程度で5barになる』くらいには変わるかもしれません」はこのようにして計算したものです。
ラテックスの漏れ速度の温度依存性について
ラテックス(Vittoria Latexの製品の方)の空気透過性の温度依存性に関するデータは、現時点では見つけることができていません(メーカーではおそらく把握しているだろうとは思いますが、表に出てくることはないでしょう)ので、近いと考えられる、天然ゴムの文献値を参考に考えてみます。
下の図は天然ゴムのガス透過度の温度による変化を、文献値を元にグラフ化したものです。酸素(O2)、窒素(N2)、二酸化炭素(CO2)のデータのプロットと、これは文献中にはありませんが、窒素:酸素=80:20の仮想空気(Air)の値を計算した値も参考までにプロットしています。
ここで、透過度は「単位面積、単位厚さ、単位差圧、単位時間あたりの基準環境(0℃、1気圧)におけるガス透過量」を表したものです。透過度がゴムの素材として徹底的に規格化された物性値(性能)であるのに対し、「漏れ速度」は個々のタイヤに取り付けた状態での性能を表しています。
透過度と漏れ速度は、ちょうど材料の剛性率と製品としての剛性、と似たような関係になります。したがって透過度の性質は、そのまま漏れ速度の性質にもあてはまります。
さて、グラフを見て何となく察する方もいらっしゃると思いますが、変化はゆるやかですが、実はゴムのガス透過度は原則として温度とともに指数関数的に増加します(漏れ速度も同様)。
ここで仮想空気の値に注目すると、25℃から50℃の間で透過度がおよそ3倍になっているのが分かります(解析すると計算上は「25℃差で3.2倍」ですが、後述する理由もあってここでは簡単のため単純に3倍とします)。
指数関数的ということは、透過度は温度の関数として
Q(T)=Q0eμT
の形で表せるということになります(もちろん例外が生じる場合もあるかもしれませんが、ここではこれ以上深くは考えないことにします。あと、学術的には上式の指数部分は活性化エネルギーEを使ってexp(-E/RT)の形で書くのが普通ですが、本稿では簡単のためこのような記述としています)。
したがってµの値が既知ならば、漏れ速度も同じ係数を使って
λ(T)=λ0eμT
の形で表せることになります。
ここで
c(T)=eμT
とおくと、任意の温度での漏れ速度λは、下の式のように、基準環境の漏れ速度λ0とcの積で簡単に表すことができます。
λ(T)=λ0c(T)
このcをここでは温度補正係数と呼ぶことにします。筆者は文献値から最小二乗法でµの値を直接求めましたが、簡易的には、上の方で既に説明した通り、異なる2点の温度(例えば6℃と26℃)での漏れ速度が既知であれば、温度補正係数を計算で求めることができます。
下の表は「温度差25℃で透過度が3倍になる」場合の温度補正係数をまとめたものです。本編で最初に示したシミュレーションは、この温度補正係数を利用して計算したものです。
| 基準環境との温度差(℃) | 温度補正係数 |
|---|---|
| -25 | 0.3 |
| -20 | 0.4 |
| -15 | 0.5 |
| -10 | 0.6 |
| -5 | 0.8 |
| 0 | 1 |
| 5 | 1.2 |
| 7 | 1.4 |
| 10 | 1.6 |
| 15 | 1.9 |
| 20 | 2.4 |
| 25 | 3 |
したがって、控えめに考えても「25℃差で3倍」を大きく下回ることはないだろう、と考えてよさそうです。
参考までに、透過度の温度依存性に関して筆者が参考にしたのは下の書籍です。
J. Comyn, ”Polymer Permeability”, Springer Netherlands, 1985.
路面温度がタイヤの温度に与える影響の確認実験(予備実験)
以下は完全な余談です。
一応理系のはしくれですから、「測れるものなら測りたい」ということで、本当にタイヤの温度=気温+5℃程度になることがあるのか、やっつけですが先日簡単な実験をしてみました。
タイヤの温度を測る方法はいろいろ考えられますが、最も単純で正確そうな方法としては、極細の熱電対(温度センサー)をタイヤの内側と外側に何か所か設置して、乾電池で作動する小型のデータロガーをハブとスポークの間に固定して、温度をリアルタイムでモニターしながらそのまま実走する、といった方法が考えられます。
ただし、データロガー(多チャンネルのものは10万円程度かそれ以上します)を壊す可能性があるのでこの方法は怖くてとてもできません。
そこで今回は、間接的な測定にはなりますが、ボイルシャルルの法則を使って調べることにしました。もしタイヤ内のエアーの温度が上がれば(体積一定とみなせれば)その分だけ圧力が上がるはず。実験というより遊びみたいなものですが、これなら費用もゼロです。
というわけで、先日、気温29℃の風の強い昼下がり、市街地の舗装路を(走行熱の影響を無視できるよう)20km/h以下程度でとろとろと走行しました。本筋とは離れるので概略の紹介だけに留めますが、走行開始して30分後にタイヤの圧力を測定したところ、前輪が4℃分、後輪が6℃分、走行前よりもタイヤの圧力が上がっていました。してやったり、の気分です。
ただし今回の実験の圧力変化は0.1 bar以下の微妙な変化なので、使用したパナソニックのデジタルゲージの誤差(±0.1 bar)を考えるとちょっと不安です。
もちろん、うまく測れば3回測っても小数点以下2桁までほぼ同じ値が出る程度の再現性はあるので、0.1bar以下の読み取り値は全くのデタラメ、というわけではなさそうですが、いずれにせよまだ確実なエビデンスが取れた、と言える段階ではありません。
もっと条件の良い(暑くてタイヤの温度が派手に上がる)日を選んで実験をやり直してみたいところですが、残念ながら急激に秋が深まってしまい、気温と路面温度自体がさほど上がらなくなってしまいました。追実験は来夏までお預けになりそうです。
売り上げランキング: 3,420