こんにちは、onittyです。先日の「ラテックスチューブはブチルに比べてどのくらい空気の減りが早い? 実験してみました」という記事を、大変興味深く拝見いたしました。

本記事ではマスター氏の実験データを元に、誠に僭越ながら理系的な視点からの解析結果と解説を私なりにしたためてみたいと思います。なるべく数式に頼らないでハートに直接伝わるように頑張ってみますので、どうぞよろしくお願いいたします。
実験内容と実験の意義について
マスター氏の行った実験の要点をざっくりと紹介すると、
空気抜けが早いと言われるラテックスの抜けの早さが実際にどの程度早いのかを調べるために、空気圧を 7 bar充填したラテックスチューブ(Vittoria Latex)とブチルゴムチューブ(Panaracer R’Air)の空気圧の時間変化を1週間にわたって、24時間(1日)おきに測定した
…というものでした。
筆者がまず真っ先に感嘆した点は、非常に面倒な、しかも時間がかかる実験をよくやりとげたものだなぁ、という点です。個々の測定作業は簡単ではあるものの、「1週間、毎日、1日おきにタイヤの空気圧を測る」という、いざやろうと思うと実際にはなかなかできそうにない、根気がなければやり遂げることができない実験に思えたからです。
これは決して茶化しているのではなく、「実際にやろうとすると時間がかかってしかもめんどくさい」という理由で「なんとなく認知されてはいても実際のデータが少ない」という実験は、学術研究においても意外とあるものなのですよね。
では今回、一週間測定をやり遂げたことでいったい何が分かったのでしょうか?それをこれから紹介したいと思います。
実験結果のおさらい
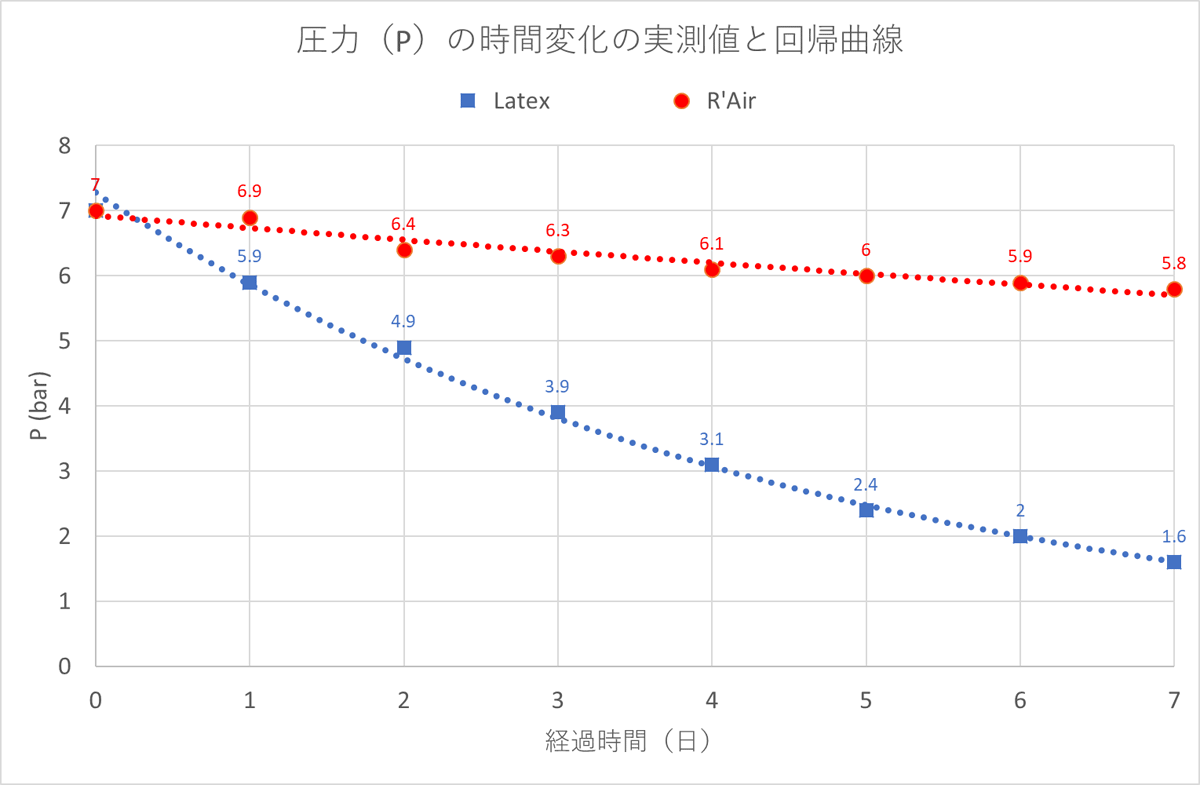
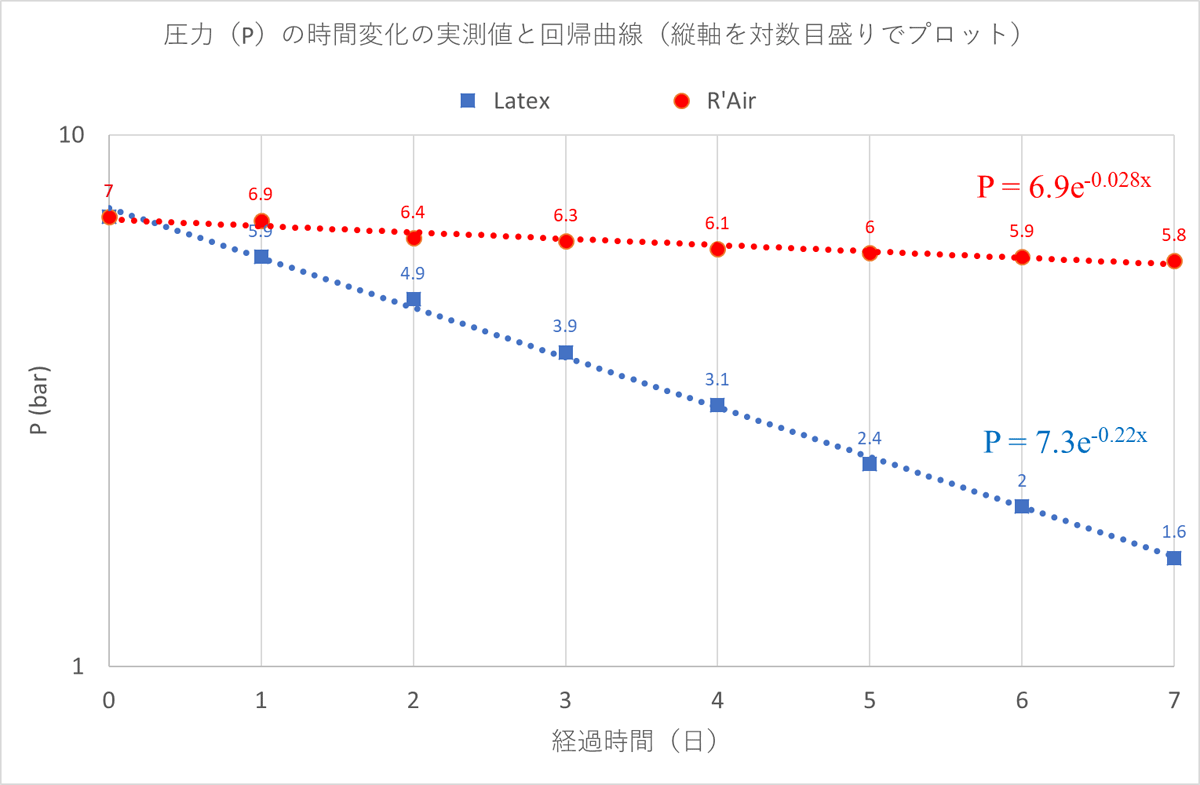
さっそくですが、マスター氏の努力の結晶(?)的なデータをグラフにしたものが下の図になります。青い点がラテックス(Vittoria Latex)、赤い点がブチル(Panaracer R’Air)の空気圧の時間的な変化を示しています。点線の補助線については、後で触れます。
マスター氏はこの結果を踏まえて、実用的な観点から以下のまとめを書かれています。特に訂正すべきことも付け加えるべきことも筆者には見つけられないので、ここでは敬意をこめてそのまま引用させていただきます。
今回の実験結果を箇条書きでまとめます。
- ラテックスは7 Barから開始すると最初の3日間、1日にほぼ1 Barづつ空気が減る
- ラテックスは1週間後には1.6 Barまで減ってしまう
- ブチルは7 Barから開始すると24時間後もほぼ減っていない(変化率で言うと1%しか減らない)
- ブチルは1週間後でも5.8 Barを保持
この実用的な解釈は、
- ラテックスはライド前に必ず空気圧をチェックしよう
- ラテックスは3日空気入れていないと相当ヤバい
- ブチルは翌日空気入れなくても全然平気
- ブチルは1週間空気入れなくてもほぼパンクリスクなし
みたいなところでしょうか。
それではこの結果を踏まえて、ちょっとだけ科学的な視点から見ていきましょう。
実験データを解析してみよう
まず、先ほどの図のそれぞれのデータ点に点線で補助線が引いてありますが、見た感じ、これらのデータ点は、どうやら直線ではなく何かの曲線に並んでいるのでは?ということが何となく分かると思います。この傾向は特に青のラテックスで顕著です。
もしこの図を見ただけで
- 指数関数的だな、と思った
- 「なぜ指数関数になるのか」という理由も予想がつく
- 頭の中に微分方程式が浮かんだ
…上記がひとつでもあてはまる方は、このあとの説明は読み飛ばして下さっても構いません。
その前に、指数関数についてちょっとだけ話をしよう
…準備はいいですね?では残りのみなさまは、とりあえず下の図をご覧下さい。今回の実験結果をシャレオツに理解するにあたって、「指数関数」だけはどうしても避けて通れませんので、まず先に指数関数について簡単に説明します。
指数関数とは y=ax といった形の式で表される関数ですが、ここでは指数関数的とはなんぞや、についてフィーリング重視で気楽に最重要ポイントだけをまるっと飲みこんでいただければと思います。数式はまったく使わないのでご安心ください。
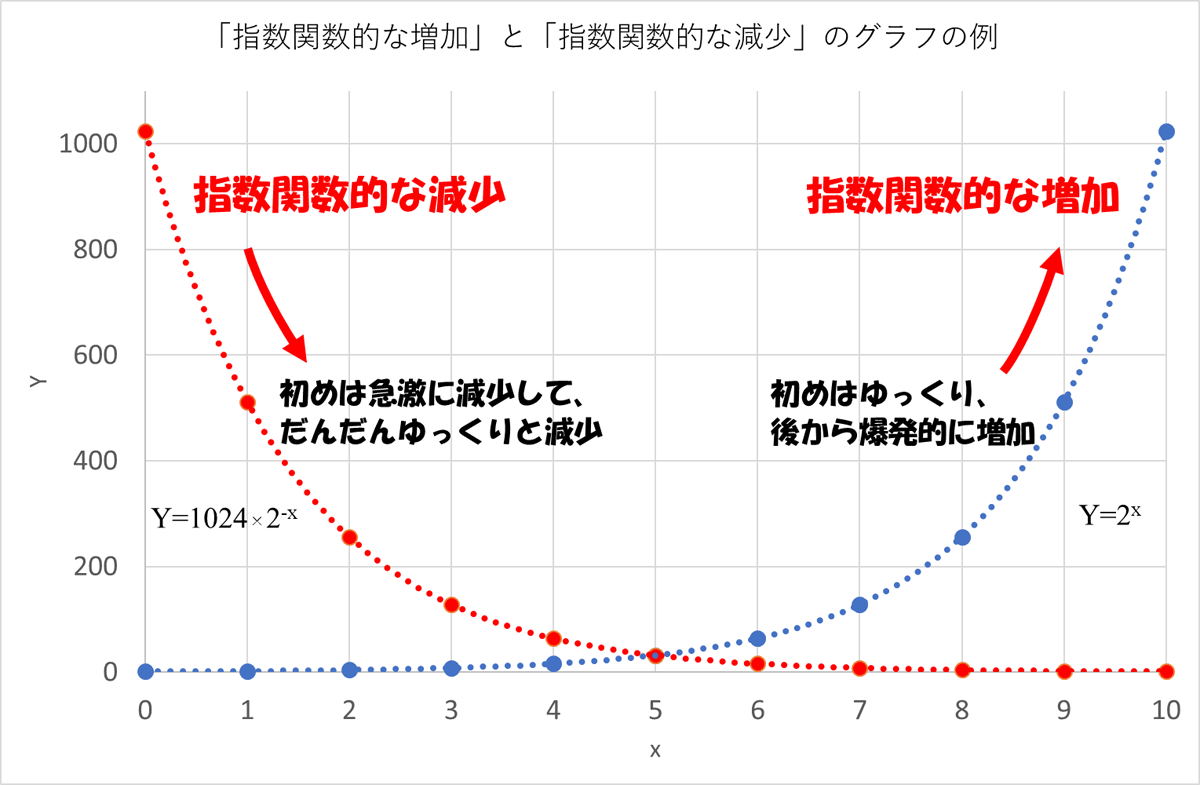
さて、図の青い点と点線は「指数関数的な増加」、赤い点と点線は「指数関数的な減少」の例を示しています。
ここで、青で示した「指数関数的な増加」のグラフは「初めはゆっくり、後になればなるほど爆発的に増加する」という特徴があります。
例えば、条件が整えば「10分に1回細胞分裂する細菌」があるとすると、初めは1個、10分後に2個、20分後に4個、30分後は8個、と初期は他愛ないものですが、3時間後にはなんと218=262,144個になってしまいます。食中毒菌は10万個以上を摂取すると症状が出るそうですので、食中毒菌がいかにヤバいかが分かりますね。
一方、赤で示した「指数関数的な減少」のグラフは「初めは急激に減少して、だんだんゆっくりと減少するようになる」という特徴があります。ちょうど青のグラフを、図の中ほどから鏡対象に左右を裏返したような形をしていますからね。
「指数関数的な減少」も放射線崩壊や化学反応、生物・医学など、自然科学のあらゆる分野でわりととありふれた現象として知られています。今回の実験結果もこの「指数関数的な減少」として理解することができるので、それをこれから納得していただきましょう。
ついでに片対数プロットの話もしよう
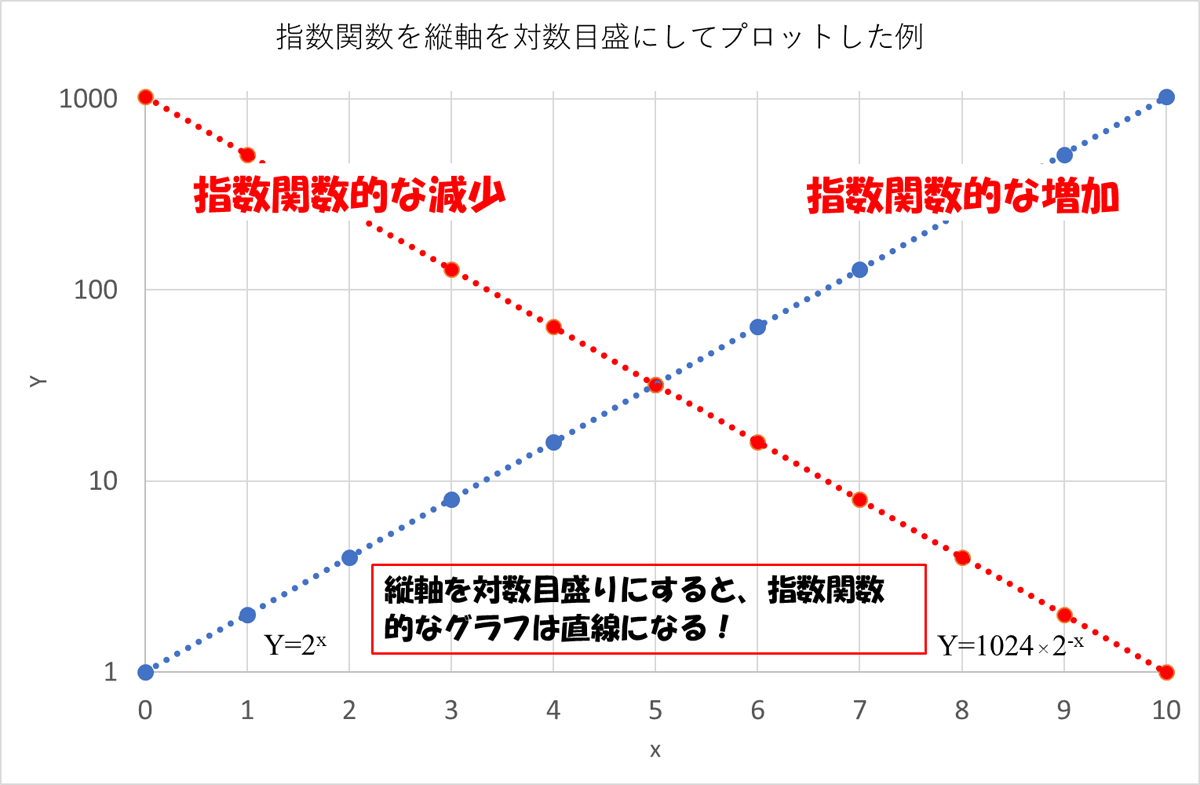
まず趣向を変えて、先ほどのグラフの縦軸を「対数目盛」に変えてグラフをプロットし直してみます。対数目盛とは、1,10,100,1000,…と等間隔で1桁ずつ増えていく目盛です。すると、前の図のグラフは下の図のように一変します。なんと、あんなに大きく曲がっていた曲線が、両方ともシャキッとまっすぐな直線になってしまいました!
このようなグラフの描画方法を「片対数グラフ」や「片対数プロット」と言いますが、指数関数は片対数プロットするとまっすぐな直線になるという特徴があります。
実験データを片対数プロットしてみよう
カンのいい方はこれから何をしようとしているかもうお分かりだろうと思います。ではさっそく、マスター氏の実験データを片対数プロットで描きなおしてみましょう。
下の図がそれですが、ラテックスもブチルも、ほぼ真っ直ぐな直線に並んでいますね。これで、この実験データ、すなわち、それぞれのチューブの空気圧の時間変化が「指数関数的な減少」で理解できることがはっきりしました。多少のバラつきはありますが、たった一回の実験であることを考慮すれば上出来でしょう。お見事です!
図の中にさりげなく数式がありますが、これは簡単な解析の結果分かった、実験データの近似式(回帰曲線)です。これまではいわば準備。次から本記事の主題である、解析結果について紹介していきます。ここからはちょいちょい数式が出てはきますが、あくまでお飾り程度なので、へぇーという感じで気楽に眺めて下さればOKです。もう少しだから逃げないで!
予測式を立ててみた
解析のテクニカルな部分はサクッと割愛させて戴きますが、結果だけ書くと、空気圧(P)の時間変化は以下の理論式(予測式)で表せます。
P=P0e-λx
ここでP0は初日(0日目)の空気圧(bar)、xは経過時間(日)、λはチューブの「空気の漏れやすさ」を表す定数で、詳しくはのちほど説明します。
eはネイピア数と呼ばれる超越数で、スマホの電卓アプリなどで、√とかπとかと同じ扱いでeとかexpと書かれているボタンがあればたぶんそれです。とりあえず指数関数を扱う際にとっても便利な値なのですが、ここではあまり深く考えなくても大丈夫です。
(Twitterでゲージ圧について情報を下さった方、ありがとうございました!)
漏れ速度を決定してみた
さきほどλについて、チューブの「空気の漏れやすさ」を表す定数と紹介しました。ここではこれを「漏れ速度」と呼ぶことにします。あまり語呂が良くありませんが、他に思いつきませんのでご容赦ください。ともあれ、ラテックスとブチルの漏れ速度の解析結果は下の表のようになりました(どうせ参考値なので、誤差などは気にしてはいけません)。
| 種類 | 漏れ速度(λ) |
|---|---|
| Vittoria Latex(ラテックス) | 0.22 |
| Panaracer R’Air(ブチル) | 0.028 |
この「漏れ速度」の意味ですが、「単位時間(1日)あたりにチューブ内の1個の空気分子が外に漏れる確率」を表しています。超ひらたく言えば、例えばラテックスの0.22という値は、初日に100%の圧力だったものが1日あたり22%漏れるくらいの勢いで漏れる=1日で78%になるくらいの勢いで漏れる、といったイメージです。
予測式を使って検証&予測してみた
ラテックスで7 barから開始した場合
したがって、ラテックスで7 barからの開始の場合、漏れ速度の値が既に分かっていれば、1日後の空気圧を単純計算で
P = 7 x 0.78 = 5.5
と考えても(1日程度なら)そこそこ近い値が計算できます。
しかしながら、実際の圧力は瞬間・瞬間で連続的に変化するので、きちんと予測するには、やはり先ほどの予測式を使ってやる方が簡単便利でしかも正確です。
さっそくやってみましょう。予測式を使う場合、1日後の空気圧は
P=7e-0.22=5.6
として求めます(P0=7、λ=0.22、x=1を代入)。実験では5.9 barですから、単純計算よりもちょっとですが近い値になっていますね。
ラテックスで8 barから開始した場合
ではラテックスで8 barから開始した場合はどうなるでしょうか?
この場合、1日後の圧力は
P=8e-0.22=6.4
となります。つまり8 barから開始すると1日で約1.6 bar減少する。これは後述する、「空気圧が高いほど抜けが早い」という性質にも合致します。
こういう解析が可能になったのは、繰り返しになりますが、地道に系統立てて収集されたデータがあってこそ、なのです。
ラテックスで5 barから開始した場合
ついでに5 barから開始した場合もやってみましょうか。この場合は、1日後の圧力の計算値は
P=5e-0.22=4.0
になります。実際、実験結果でも2日目の4.9 barから3日目に3.9 barとなっていて4.9 barからにはなりますが1日で1.0 bar減少していますから、ほぼほぼ近い値ですね。どうです?これがカガクの力です。
解析結果を利用する際の注意点
筆者はゴムは専門外なので少々調べてみましたが、この漏れ速度は
- チューブの厚さ
- 温度
の影響で値が変わるらしいです。直感的には、チューブの厚さが薄くなるほど、あるいは温度が高くなるほど空気の漏れは早くなるだろう、と推測できます。したがって漏れ速度の値は、同じ銘柄のチューブであっても、組み合わせるタイヤサイズやホイールのリム幅、季節(外気温)の影響、等々によっても変わる可能性があります。
その他、マスター氏も指摘したように、走行することで静置状態よりも漏れ速度が早くなる可能性も考えられますし、場合によっては素材の経年変化の影響や、サンプルの個体差(製造工程や取り付けの出来・不出来)も考える必要があるかもしれません。もちろん製造メーカーや商品銘柄(素材の違い)についても同様でしょう。
解析結果のまとめ
今回の解析結果を箇条書きでまとめます。
- 実験結果を片対数プロットすることで、チューブ内の圧力の時間変化は指数関数的な減少であることがビジュアル的にはっきり示せた
- チューブ内の圧力の時間変化を表す理論式を決定した
- ラテックスとブチルのそれぞれの「漏れ速度」の値を決定した(ただしマスター氏の実験条件において、という制限付き)
- 理論式と漏れ速度の値から得られた予測式を使って、7 bar、8 barや5 barから開始した場合の「圧力の時間変化の推定値の計算方法」を参考例として紹介した
ただし、推定値がどの程度現実をうまく予測できるかについては今後の検証が待たれます。
空気がチューブを透過するようすをイメージしてみよう
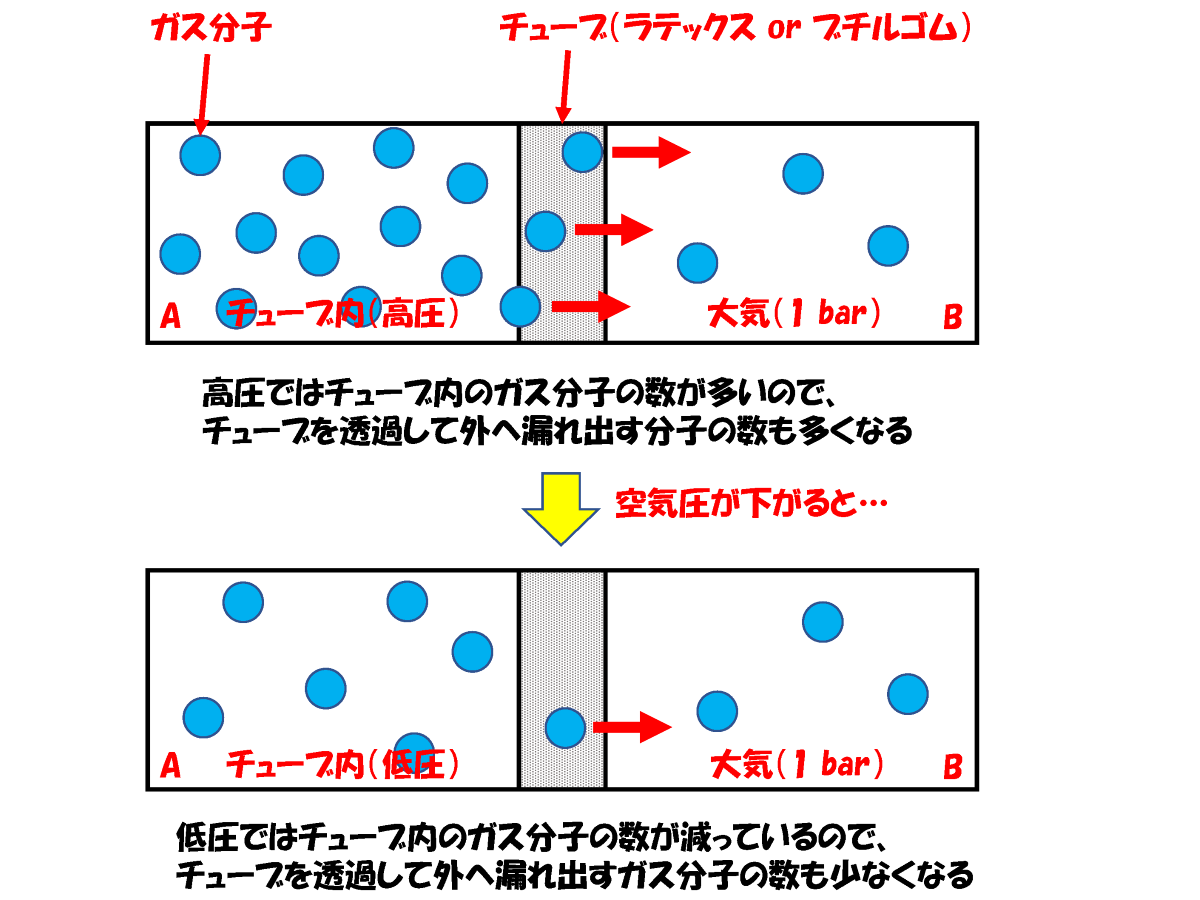
最後に、下の図でこの実験の物理的なイメージをどう考えればよいかについて説明します。
左側のAの部屋(チューブ内)と右側のBの部屋(大気)の間に、チューブの壁があるという単純なモデルを考えてみましょう。
ラテックスもブチルも、速いか遅いかの違いはありますが、どちらもガス分子(ここでは酸素、窒素、二酸化炭素などの空気中の分子をまとめてガス分子と呼ぶことにします)を透過する性質があります。
ガス分子はチューブの壁以外は通り抜けることはできないものとしますが、Bの部屋は大気なので、圧力は常に一定(大気圧)と仮定します。
ガス分子は当然、圧力の高い方から低い方へ通り抜けることになりますが、温度や壁の厚さなどの他の条件が一定であれば、1個のガス分子が壁を通り抜ける確率は一定です。ということは、Aの圧力が高いほどガス分子が数多く存在しますから、それだけ多くのガス分子が壁を通り抜けてBへ漏れ出ることになります。
一方で、Aの空気が抜けて圧力が下がると、チューブ内部のガス分子の数も高圧のときに比べれば減ってくるため、その分チューブの壁を通り抜けて漏れ出るガス分子の数はだんだんと少なくなってきます。
これは既に説明した「初めは急激に減少して、だんだんゆっくりと減少する」指数関数的な減少の特徴とまさに同じ特徴ですね。
というわけで、細かい話は省略して結論だけ言うと、上で説明したような物理的なイメージをビブンホウテイシキという技術を使って数式をこねくり回すと、「空気圧の減少速度(空気圧の時間変化率)が空気圧に比例する」という法則が成り立つと仮定することができて、最終的に、圧力の時間変化が前述のP=P0e-λxという指数関数的な減少の式で表せるという考えにたどり着くのですが、ビブンホウテイシキを説明しようとするとさすがに読者が指数関数的に急激に減少していく気がするので、今回はこの辺でそろそろおしまいにしたいと思います。
ブチルチューブについて
終わりが近づいていますが、ブチルに関してちょっとだけ。
ブチルは1週間放っておいてもほぼパンクリスクなし、ということで予測する必要性も乏しいことから解析ではあまり触れませんでしたが、もしもブチルを前回より精度よく調べたいならば、ブチルに限っては2週間程度のスパンで圧力変化を調べてやるとよりベターかもしれません(ブチルの圧力変化は非常にゆっくりなので、7 barから開始の場合、14日目でようやく5 barを下回るかもしれない程度でしょう)。
その場合は、最終日まで1日おきに15回まじめに測定する必要は無く、2日(48時間)おきに測定してやるくらいでも実験としては十分に思えます。
まとめ
- マスターの実験結果の解析を通して、個人でもチューブの「漏れ速度」が簡単に(?)求めることができることを紹介しました。
- 「漏れ速度」が分かれば、チューブの空気圧の時間変化を、まあまあの程度には予測可能であることを紹介しました。
- ぶっちゃけ、実際にチューブの空気圧の運用管理上でやるべきことは、今回の解析結果を見る前と後で全く変わるところはないであろうことに気づきました。