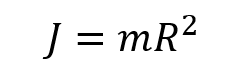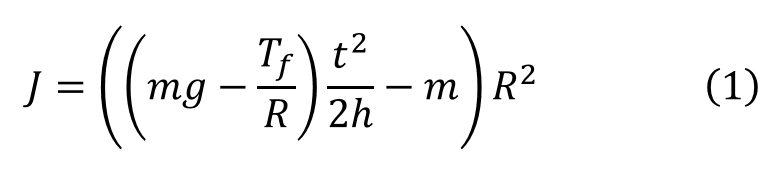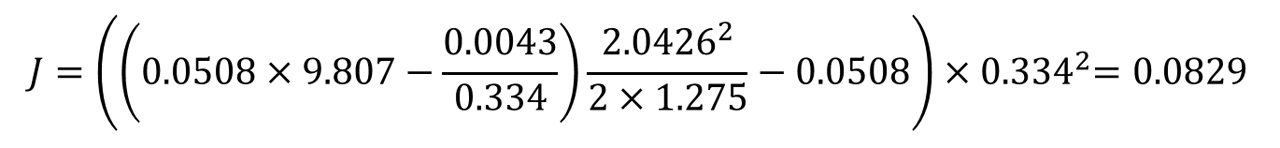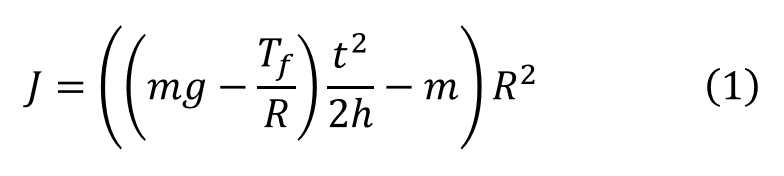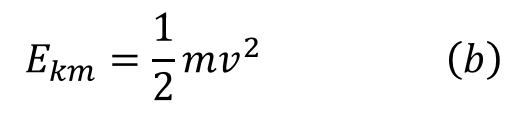慣性能率忍法帖外伝

よし子　「えーっ、何、入り口の怪しい貼紙　キモくて引いちゃう～」
宅浪　「ヘンな自転車屋だ」
よし子　「いい感じのウエアとかぜったい扱ってなさそう」
宅浪　「やめておこうよ・・・って言ってるのに何で入っていくんだよぉ！」
よし子　「くつしたとかあるんですかぁ～？」
店主　「はい～、ありますよ　どうぞどうぞ」
宅浪　「何だ、ふつうにあるじゃん」
よし子　「あのぉ～　表の貼り紙、あれは魔除けか何かですか？」
宅浪　（ｱ―ｯ、ダメだってそういうこと訊いちゃ）
店主　「ええまあ・・・」
宅浪　「えーっ、マジですか　どういう魔除けなんスか？」
よし子　「初心者を大切にしてるんですね」
宅浪　（ええーっ！？）

何だか導入がヘンテコですが、ご容赦ください。お題は 「慣性モーメント」

慣性モーメントというと、「ホイールの慣性モーメント」などという使い方、しますよねぇ。英語表記でmoment of inertia、コレの和語が慣性モーメントで、慣性能率などと言われることも。何なんですかねぇ、慣性モーメント。このお題でいろんなウンチク、方々から聞こえてきそうです。

A氏　「さすが小径車。ホイールの慣性モーメントが小さいからスタートダッシュが効くぜ！」

B氏　「タイヤはホイールの最外周についているから、慣性モーメントの影響で軽量化の効果が顕著なのさ」

C氏　「近年、だんだんレースタイヤが太くなってきたが、慣性モーメントの差は実はほとんどない」

D氏　「いや、そんなことはない。差はしっかり実感できるが、それ以上にコーナリングのスタビリティを優先するようになったんだよ」

全部本当で全部ウソ？その真意は如何に！

慣性モーメントの定義
ホイールの慣性モーメントを測定する
慣性モーメント計算式の導出
700CとETRTO451再び
平行軸の定理
まとめ

慣性モーメントの定義

慣性モーメント (moment of inertia) は慣性能率とか、単にイナーシャなどと省略して呼ぶこともあります。なおイナーシャという言葉は、真っ直ぐ動いているものにも使います。

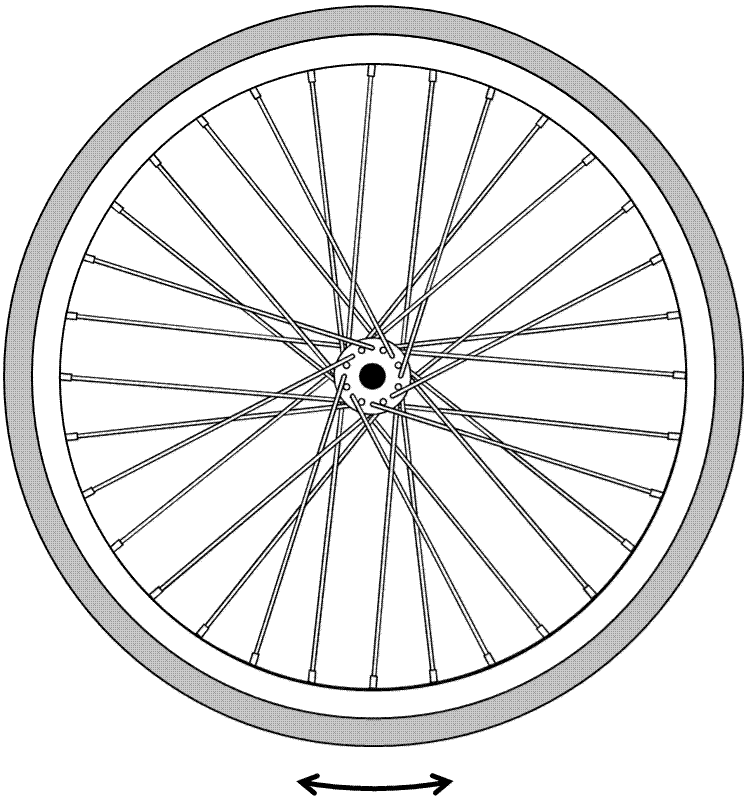
例えばホイールがぐるぐる回転している様子を想像します。ハブシャフトの中心の周りをリムやタイヤがぐるぐると回っていますよねぇ。

「慣性モーメントって、何処の？」

と訊かれたら、この場合は

「ハブ軸を中心として、その周りの」

と答えることになります。これで、慣性モーメントの対象が、ハブ、スポーク、リム、タイヤなど、ハブ軸周りを一体で回る構造物であることが明示されます。まさか、ホイールを掴んで自転車本体をグルグル回す人はあまりいませんから、これでいいんです(笑)。

ホイールの中心軸の周りの慣性モーメント

ある回転軸から距離Rメートルのところにある一個の重りmキログラムの慣性モーメントJは、

です。なぜこうなるのか、というのも知っておくとよろしいかともいますが、ここでは天下り式でこの式を肯定します。すると、同じ質量mであっても、中心軸からの距離が大きいほど、慣性モーメントJが大きくなることがわかります。しかも、距離Rの2乗で効いてきますから、大径ホイールほどJが大きくなります。

上の図では、ホイールの最外周にタイヤが、そのすぐ内側にリムが位置しています。慣性モーメントJが距離Rの2乗で効きますから、タイヤとリムの寄与率が飛び抜けて高いということがわかります。

一方でハブ。これは中心近傍に集中していますから、かなりの重量物であったとしても、寄与率は極めて低くなります。

スプロケも同じ。例えば12-28の11sスプロケが400グラムだったとして、仮に、半径が5cmということにして過大評価しても、J=0.4×0.05^2=0.001、一方で350グラムの25Cタイヤの慣性モーメントは0.037ですから、スプロケの慣性モーメントはタイヤの3%以下程度にしかなりません。

さて、例えば700Cホイールと、ETRTO451の20インチホイールで、同じ銘柄の25Cタイヤが装着されている場合を仮定しましょう。この時、ハブ軸周りのタイヤの慣性モーメントはどうなるか？700Cタイヤが丸断面だったとして、その断面中心からハブ軸芯までの距離が0.324m、ETRTO451の場合が0.238mであったとします。この場合、半径Rの比は

半径比率 = 700C：ETRTO451 = 0.324：0.238

さらに、タイヤ周長も同じだけ異なるので、質量mの比も考えると

質量比率 = 700C：ETRTO451 = 0.324：0.238

というわけで、慣性モーメント J = ｍR^2 の比率は

慣性モーメント比率 = 700C：ETRTO451 = 質量比率×半径比率^2 = 0.034：0.0135

つまり、700CタイヤはETRTO451タイヤと比較して実に2.5倍の慣性モーメントになります。リムも同銘柄ならば、ほぼ同じ話で、700CリムはETRTO451リムの2.5倍程度の慣性モーメントになります。ホイールの慣性モーメントはタイヤとリムに大きく支配されますから、700CホイールはETRTO451ホイールの約2.5倍の慣性モーメントになります。

さあ、以上の論考を受けて、

「おおーっ、小径車の加速、期待大！」

と考えるか、それとも

「実走上の差はないね」

と考えるか・・・。

700CとETRTO451のホイールで大きな慣性モーメントの差がありそうだということは分かりましたが、それがどんな意味を持つのか？そのあたりも多少考えながら、ホイールの慣性モーメントを実測してみましょう。

ホイールの慣性モーメントを測定する

平地を一定速度で走行する場合、自転車と乗り手は、

空気抵抗
タイヤ転がり抵抗

を受けます。したがって乗り手は、これら（に加えてギヤなどの損失）の合計に見合った出力をクランク軸に与えていることになります。人と自転車の重量に着目すると、平地を一定速度で走行する場合、重量が走行抵抗に与える影響は、タイヤの転がり抵抗成分への寄与がそのほぼすべてです。

したがって、平地を定速で走行する際には、タイヤの種別やグレード、銘柄、空気圧や、フレームのリアクションが気になることはあっても、車重が気になることはまず、ありません。ホイールの慣性モーメントに至っては、転がり抵抗も何も、全く関係ありません。しかし、加減速走行する場合には、上の①②に加えて、

質量加速抵抗

が新たに加わるため、車重や体重が重いと、加速時にはその分だけ人間の出力が余計に必要になります。また、ホイールに着目すると、慣性モーメントという「質量の親戚みたいなもの」がなぜか、「加速の時だけ」顔を出し、さらに仕事が増えます。

一般論としては、剛性が同じで、乗り手の入力に対して同じような反応を示す自転車であれば、車重は軽い方が加速が良く、慣性モーメントが小さい方が加速が良い、ということになります。ロードホイールの場合、満足できる剛性が確保できているのならば、慣性モーメントが小さい方がよいのは明白でしょう。

・・・あっ、ホイールの軸周りの慣性モーメントを計測するんだった。

パーツの重さと寸法を測って適当に概算するという方法が最も簡便で、精度的にも全く問題ありませんが、以下に紹介する方法は、計測方法として比較的簡便だと思います。興味のある方は、どうぞ！

測定方法

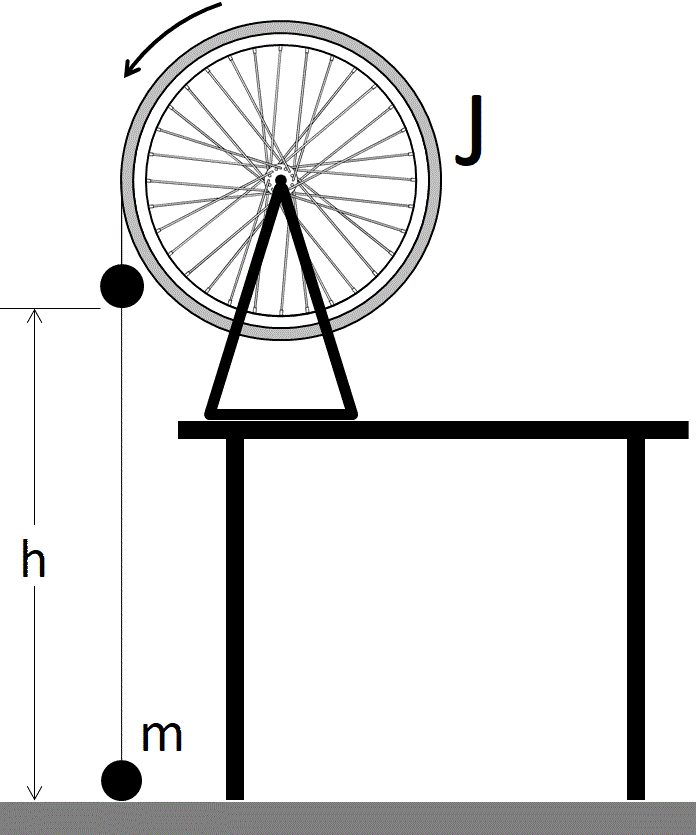
下の図のように、前ホイールの外周に糸を1周ほど巻きつけて、この糸にくくりつけた質量mのおもりが床から高さhのところに位置するように、ホイールを手で軽く支えます。次に、手を離すと、ホイールが回り始めて、おもりが落下していきます。hだけ落下して床に衝突しますが、手を離した瞬間から衝突までの時間は、慣性モーメントJの値が大きいほど、長くなります。

というわけで、落下時間を計ることで、ホイールの慣性モーメントを求めることができます。その次の画像は実際に行った実験系の様子です。

実験の概念図

実験のようす

準備するもの

ホイール：手持ちのホイール(前後どちらでも)
おもり：今回は500円玉が8枚
秤：おもりの質量を計ります
糸：普通の手縫いの細い糸ではなく、ちょっと太めがやりやすい
ホイール支持台：フレ取り台や自転車ディスプレイラックなどなど
ストップウォッチ：時間を計る小道具

実験手順

おもりの質量mを秤で計測します
おもりを付けた糸をタイヤに巻き付けます
おもりを落下させる落差hを巻尺で測ります
高さhにおもりを保持した状態からホイールを解放し、この瞬間にストップウォッチを押します
床などに衝突する瞬間にストップウォッチを止めて、落下時間tを測ります

以上で、

m：おもりの質量[kg]
h：落下距離[m]
t：落下時間[s]

がわかりましたが、これに加えて

R：糸を巻き付けたタイヤ外周の半径
g：重力加速度 ( 9.807 [m/s^2] )
Tf：ホイールの軸フリクション [Nm]

も使います。ただし、ホイールの軸フリクションは不明ですので、とりあえず零ということにしておきます。

慣性モーメントを計算する

慣性モーメントJは次の式(1)を使って算出します。

いきなりこんなものが出てきたら、半端なく天下りで納得できませんが、とにかくこの式に先ほどの数値を代入します。この式の出自を知りたいという方や、夏休みの自由研究でこのネタを使いたいという探究心旺盛な中高生の方は後ほど。。。

実験結果

私が行った実験の結果を以下に示します。なお、今回用いたホイールは前輪で、リムがAMBROSIO NEMESIS 32H、スポークがDT-SWISS Champion 1.8、真鍮ニップル、ハブがSHIMANO HB-6700、タイヤがVittora CORSA CX ELITE 21C、リムセメントがSOYO、ハブ毛が（えっ？）・・・です。

使用した数値は以下の通り。

質量 m = 0.0508 kg （500円玉8枚＋ビニールテープ10cmなど）
落下距離 h = 1.275 m
重力加速度 g = 9.807 m/s^2 → これは常にこの値を使います
ホイール半径 R = 0.334 m
落下時間計測5回 t = 2.040, 2.041, 2.045, 2.042, 2.045
→ すべて有効値として採用し、平均値は t = 2.0426 s
ホイール軸フリクション Tf = 0 Nm (とりあえずゼロとしておきます! )

以上の数値を式(1)に代入して、慣性モーメントJとして0.0853 kgm^2を得ました。
　　

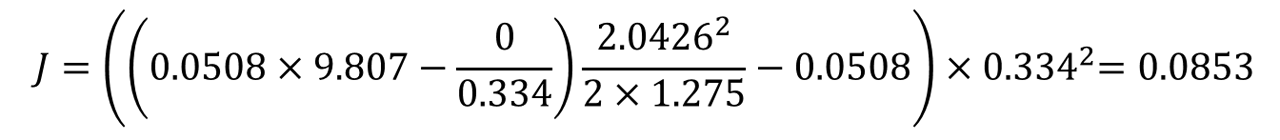
ホイール軸フリクションの扱い

さて、式(1)でホイール軸フリクションTfを零としましたが、それはどうにも気持ち悪いですね。実は、このTfはかつて計測したことがあります。その値は

Tf = 0.0043 Nm

今度はこの値Tfを式(1)に代入してみると、
　　

となります。慣性モーメントが先ほどの値から修正されました。というわけで、私のロードバイクの前ホイールの慣性モーメントは、
　　

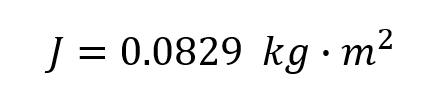
となりました。軸フリクションを零とした最初の値に対して97.2%の数値を示しており、多少、小さくなりましたが、軸フリクションが測定結果に及ぼす影響はこの程度のモノなのだ、ということもわかりました。

とりあえずこれが、このレビューの終着点です。最終的な値としてコレを採用することにします。

時間の高精度計測

今回の実験では、ホイールを停止させていた手を離した瞬間にストップウォッチを押し、重りが床に当たった瞬間にもう一度押すのですが、ストップウォッチで落下時間を計測するのは難しい、という感想を持ちました。やるたびに数値がバラつきます。

「ちゃんと計測できてる気がしねぇ～～」

という感じ。
陸上の時間計測ではメキシコ五輪（1968年）あたりからだったか、電気計測が導入され始めましたが、100mのスタートでは手動時計を押すのが遅くなり、ゴールではつい早めに押してしまって、時間が少しだけ短くなっちゃったりするんですよね。電気計測と手動計測で0.24秒程度も差があるとか？

重りが床に落ちたその瞬間にストップウォッチを押しているつもりなのですが、動体視力の衰えを隠せない年頃の私は、どうしても早めに押してしまうし、押すタイミングもばらついてしまい、もうマジで手に負えないダメすぎる精度の時間計測にしかならないんですよねぇ。

というわけで、音で計測することを考えました。実は上の実験では、この「音計測方式」を使っています。おかげで5回の計測数値のばらつきが手動計測と比べて俄かに信じられないほど小さくなってしまいました。

やり方は簡単です。まず、ホイールを止めている手を離した瞬間に、棒で机を「カン!」と叩きます。このタイミングは、何かとおぼつかない自分でもうまくいきます。次に、おもりが床に落ちた瞬間に「コン!」という音が出ます。この2つの音を録音して、その波形の立ち上がり時刻から時間間隔を読み取ります。

音速が有限であることも侮れませんから、マイクロフォンを2つの音源から同じ距離に置くと良いでしょう。

SoundEngine Freeで波形を確認する

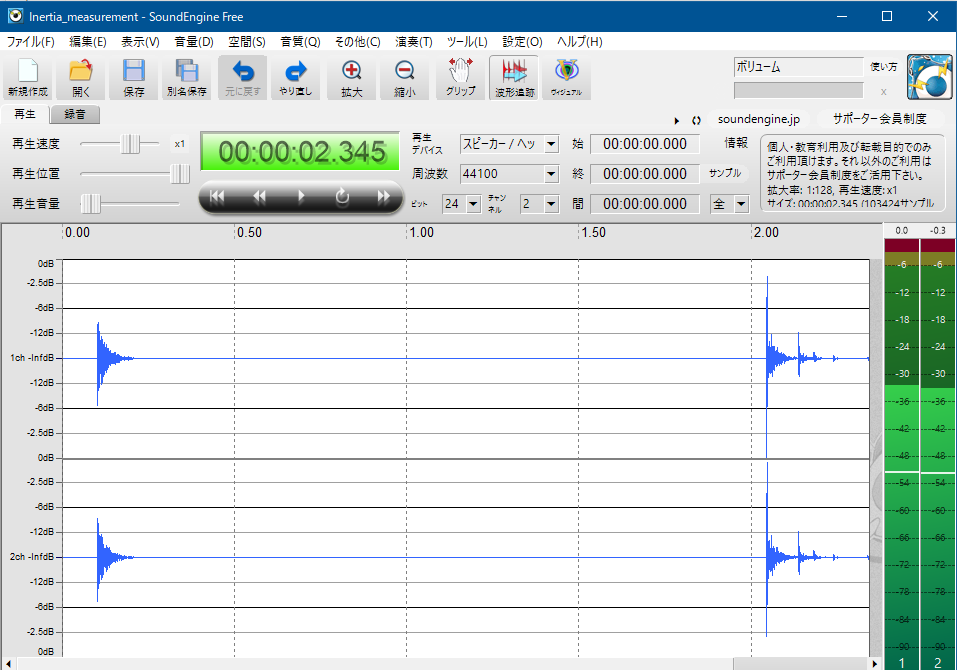
スマホやノートPC内臓のマイクやPCMレコーダなどで録音します。wavファイル形式で録音した波形を見るには、フリーソフトの　”SoundEngine Free”　が便利です。再生画面で波形を見ると、例えばこんな風になります。

SoundEngine Freeの波形

これは手を離す瞬間の音と、おもりが床に衝突する音が両方捉えられていますが、時間軸を拡大して音が立ち上がる瞬間の時刻を例えば1/1000秒刻みで細かく見ることが出来ます。こんなソフトが自由に使えるとは、世の中、便利になったものです。

これはSoundEngine Free本来の使い方ではありません(笑)

なお、スマホ録音した音声がwav形式でない場合は、必要に応じてフリーソフトでwavに変換してからSoundEngine Freeに投入します。

慣性モーメント計算式の導出

慣性モーメントの計算式(1)の導出過程を説明します。

以下に式(1)を再掲します。こんな式を天下りで使えなんて、冗談じゃねえぞ！ですよねぇ。

まず、質量mのおもりの最初の位置は高さhですので、このおもりは、重力場での位置エネルギーとして、下に示す式(a)のようにEpというエネルギーを持っています。
　

ホイールを止めている手をパッと離したその瞬間から、おもりによってホイールが回転し始め、段々回転速度を速めながらおもりが床に衝突します。おもりがhだけ降下して今まさに床に衝突するぞ、という瞬間のおもりの速度をvとすると、このおもりは式(b)のような運動エネルギーEkmを持つに至ります。

また、ホイールが回転しているので、回転速度をωとしてホイールの慣性モーメントも式(c)に示す運動エネルギーEkjを持つに至ります。

式(b)と式(c)は同じ形をしていて、mとJが対応しています。なるほど慣性モーメントは「質量の親戚みたいなもの」ですねぇ。

次に軸フリクション。

軸フリクションTfは、エネルギーを消費します。軸フリクションによる損失エネルギーは軸フリクションと回転角度の積で与えられます。回転角度というのは、この場合、タイヤ半径Rで高さhを割ったもので、角度単位はラジアン[rad]ですが、これらから、軸フリクションによる損失エネルギーEfは式(d)のように与えられます。

以上で4個のエネルギーが出てきましたが、これらには式(e)、(e’)のような関係があります。

　　
この等式(e)の読み方は、例えば、

最初におもりmが持っていた位置エネルギーEpを使っておもりmが加速しつつhだけ降下したことで、位置エネルギーEpは、おもりの運動エネルギーEkm と、ホイールの運動エネルギーEkjに変化したのだが、嗚呼、残念なことにホイール軸フリクションEfの分だけ損しているから、左辺でまずそれを控除しておかなければ

という風になります。

さて、おもりが加速度aで降下していたとすると、床への衝突速度vと到達時間tの関係は式(f)、

　　
速度を時間で積分すると落下距離になりますから、高さhと加速度aと到達時間tの関係は式(g)、

　　
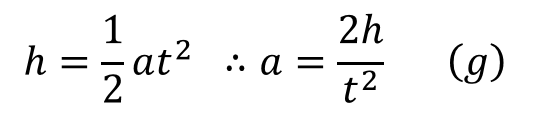
また、おもりの速度vとホイールの回転角速度ωはホイール半径でつながっていますので、vとωの関係は式(h)となります。

　　
したがって、(f)(g)(h)から速度vと角速度ωを式(i)のように書くことが出来ます。

　　
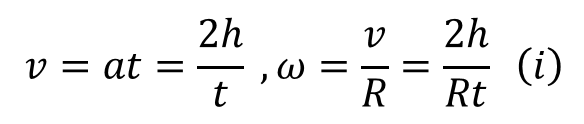
式(i)のvとωを式(e’)に適用して変形することで、式(j)を得ます。

　　
式(j)は、最初の式(1)と同じです。

700CとETRTO451再び

この拙文の最初の論考で、

つまり、700CタイヤはETRTO451タイヤと比較して実に2.5倍の慣性モーメントになります。リムも同銘柄ならば、ほぼ同じ話で、700CリムはETRTO451リムの2.5倍程度の慣性モーメントになります。ホイールの慣性モーメントはタイヤとリムに大きく支配されますから、700CホイールはETRTO451ホイールの約2.5倍の慣性モーメントになります。

と書きましたが、この話にはトラップが仕込まれています。

700Cホイールの慣性モーメントはETRTO451ホイールの約2.5倍になるのですが、走り出しの加速に対する影響も2.5倍になるかというと、実は、そうなりません。

ゼロスタートで同じ車速まで加速したとすると、その時のホイールの回転速度に差が表れます。当然のことながら大径の700Cホイールの回転角速度が遅くなります。ホイールの回転エネルギーの式(c)を再掲します。大径ホイールではコレの回転角速度ωがゆっくりになるわけです。

　
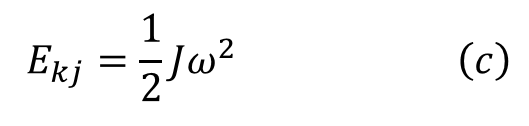
ホイールの慣性モーメントが軽いので漕ぎ出しが軽い、というのは、加速して車速ｖに到達した瞬間の式(c)の値が小さい、つまり、同じ車速なのに少ない運動エネルギーしか与える必要がない、という意味ですから、回転角速度ωに関しては、700Cの方が小さい値を示すので「軽い」ということになります。

しかし、慣性モーメントJは700Cの方が大きい値を示すので「重い」ということになります。ホイール半径の比率と質量の比率を思い出しますと、

半径比率 = 700C：ETRTO451 = 0.324：0.238
質量比率 = 700C：ETRTO451 = 0.324：0.238

これを使って慣性モーメントの比率が

慣性モーメント比率 = 700C：ETRTO451 = 質量比率×半径比率^2 = 0.034：0.0135

でしたが、これに加えて回転角速度の比率も考えると、

角速度比率 = 700C：ETRTO451 = 0.238：0.324

となります。式(c)の　Jω^2　のJに慣性モーメント比率、ωに角速度比率を代入すると、

Jω^2 = 慣性モーメント比率×角速度比率^2 = 0.00193：0.00142