スポークテンション計測用ツール、そしてヴァイオリンの弓

GlennGould (守衛のおじさん) です。突然ですが、

《スポークテンション計測用ツール》 と 《ヴァイオリンの弓》

この2つをつなぎ合わせてみます。ちょっと入り組んだ読み物になってしまいましたが、暫し、お付き合いの程、よろしくお願いいたします。

ParkTool TM1～本稿の目的

スポークテンション計測用ツールと言えば、簡潔で手軽に使えるParkToolのTM-1が有名です。手ごろな価格で使いやすく、多くの種類のスポークに対応しています。参考までにCBN本館のTM-1レビューから、2編を選んでおきます。

cbn Park Tool TM-1・・・構造と計測原理編
cbn Park Tool TM-1・・・実用編

上レビューはかなり面倒な内容ですが、TM-1の動作原理の理解に格好の素材なので、ご興味のある方、よろしければ是非ご覧ください。

一方で、大雑把に捉えるという目的で、スポークの打撃音によりテンションを経験的に推定する、ということも従来から行われていました。

ハブ穴からリムの穴にかけて張られ、ニップルを締めあげることでテンションが付与されるスポークはそれ自身、紛れもない弦であり、ギターやヴァイオリンの弦と類似の、弦としてのある種の振動様式(モード)を呈すると考えられます。

本稿では、このスポークを弦と見立てて打撃したり、爪弾いたりしたときに発せられる音の周波数からスポーク張力を推定することが可能かどうか、確認してみます。

また、ヴァイオリンの弓でスポークが発音することを示し、これによる音高同定と、スポーク張力推定器としての評価を行います。

弦の振動周波数

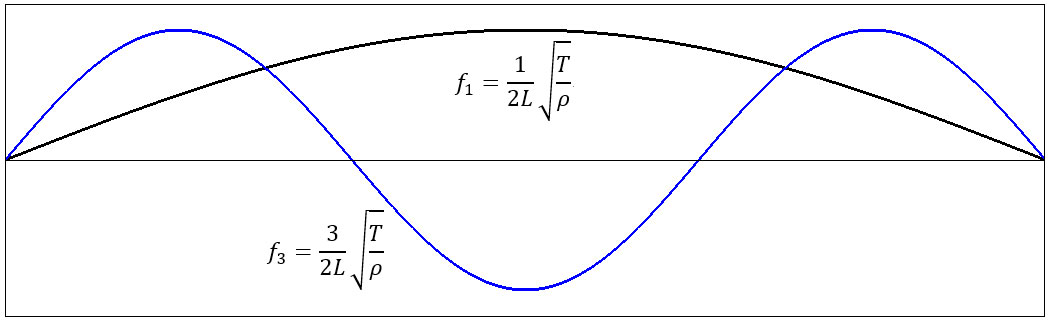
2点固定された、ごく普通の弦の基本的なピッチ、つまり音高、すなわち振動周波数f1は、弦の張力T、弦の線密度ρ、弦の長さLによって次のように記述されます。

なお、周波数f1の単位はHz(ヘルツ：1秒間の繰り返し回数)、張力Tの単位はN(ニュートン)、線密度ρの単位はkg/m(キログラム毎メートル：メートル当たりの質量)、長さLの単位はm(メートル)です。

また、地上の質量1kgの物体には重力加速度によって9.806Nのちからが落下方向に働きます。

この9.806 m/s^2は重力加速度という数値で、単位はm/s^2、つまり加速度の単位を持ちます。したがって単位Nは単位kg*m/s^2と等価です。

上の式の右辺の単位を計算してみると、周波数すなわち ”Hz” つまり ”1/秒” になっています。

この式は、ギター弦のような、ごくシンプルに振動する弦の運動方程式から抽出されます。

ただし、見いだされる周波数の数は、実は無数に存在し、上の式は、その中で一番、値が小さいもの、すなわち1番目「基本次数」に相当するもの、ということになります。

ギターの弦を中央ではじくと、1番目以外に、3番目や5番目以降も強く励起されます。1番目の波は下図の黒線、3番目の波は青線で示されます。もし、黒線の波が100Hzだったとすると、青線は300Hzの波を示しています。

先ほどの式からは、弦の線密度、つまり単位長さあたりの質量ρ(kg/m) が大きいほど、また、張力T(N) が小さいほど、低い周波数の音が出ることが分かります。

硬いピアノ線に銅線をグルグルと巻き付けて重くして、振動周波数を低くすることができますが、これはρ(kg/m)を大きくすることに対応します。実際、ピアノの低音側の弦は、そんな風になっています。

ところで、弦の断面積をA(単位はm^2)、弦の単位体積当たりの質量つまり密度をµ(単位はkg/m^3)とすると、単位長さあたりの質量ρ(kg/m)は

ですので、

となります。

試しに、この式のL、T、µ、Aをそれぞれ現実のスポークで示してみます。

例えばごく平凡な700Cクラシック系32Hチューブラリムとスモールフランジハブにステンレス・プレーンスポーク6本組(3クロス)を適用すると、それぞれの実効的な数値は、例えば、次のようになります

• L = 0.296 (m)・・・スポークの実効的な長さ
• T = 900 (N) ・・・スポークテンション(とりあえずの数値)
• A = 2.54(mm^2) ・・・ 1.8mmスポーク(#15スポーク)の場合の断面積
• µ = 7800 (kg/m^3) ・・・ ステンレスの密度の一般的な値

これらの数値を単純に上の式に代入すると、360Hzを得ます。

スポーク弦の特異性

ギターの弦などは、両端が基台(ナット＆ブリッジ)に点で拘束されています。非常に単純な拘束であり、弦自体は結構、自由です。

一方、スポーク。

まず、スポークは硬い。ギターの弦は金属であるとはいえ、かなり糸っぽい(?)ですが、スポークは、棒の風味。そして、拘束状態が少々異なります。特にニップル側。こちらは弦としての自由な動きを妨げるような拘束を受けています。

ちょっと想像でモノを言ってしまうと、この拘束で少し周波数が上がるんじゃないか ? という雰囲気があります。

硬いステンレス棒であるスポークの両端を強引に固定してしまうとギター弦のような素直な振動は励起されず、振動周波数が上昇することが容易に想像されます。それに、あまりきれいな音は出ないんじゃなかろうか?という雰囲気があります。

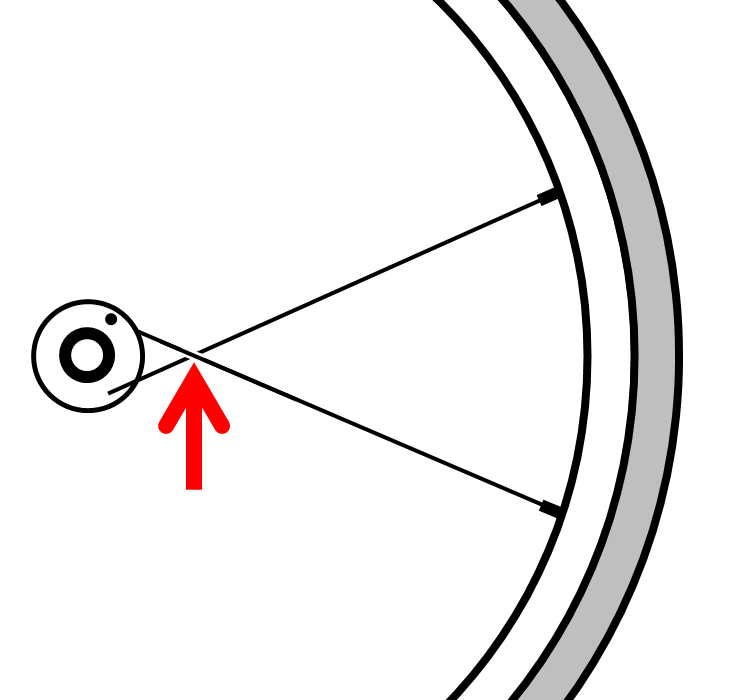
さらに、6本組みというくらいですので、1本目と6本目のスポーク交差点が、接触しています。次の図の赤矢印のポイントです。

このポイントはかなり強固な拘束点に見えます。恐らく、296mmの実効長よりも短い長さに相当するような高めの音が出てくるのではないかと思われます。

一方、交差組ではなく、ラジアル組ならば、スポーク同士の接触交差がないので、交差組よりも低い音が出るはずです。

さて、どうなることか・・・

ハンマリングによる発音

実際にプラスチックハンマーで打撃してどんな周波数が出てくるか、確認してみます。

ただし、6本組みスポークの接触交差が煩わしいので、打撃試験を行う2本だけを接触しないように組み直し、通常通りのテンションを与えたスポークを打撃しています。

つまり、スポーク接触点が無いという意味では、疑似的なラジアル組状態です。スポークはハブ穴とニップルの2か所以外での拘束は受けていません。

次の図で、左が通常の6本組み(3クロス)、右が無接触6本組み、です。右のスポークは赤矢印点で接触していません。交差点をよーく、ご覧ください。間違い探しのような図で申し訳ありません。

次に示す音が実際の打撃音。なかなかイイ感じの音が出るものですが、これを採集した時のスポークテンションは、ParkToolのテンション計”TM-1”による指示値で、731N (74.6kgf) 付近でした。

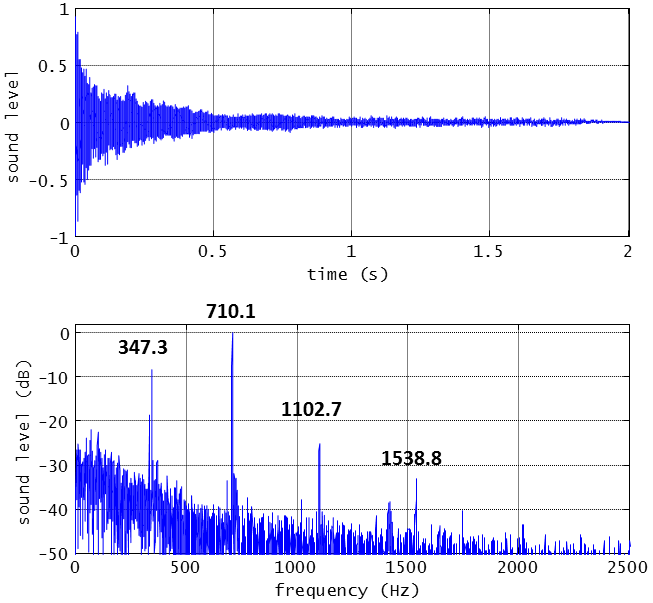
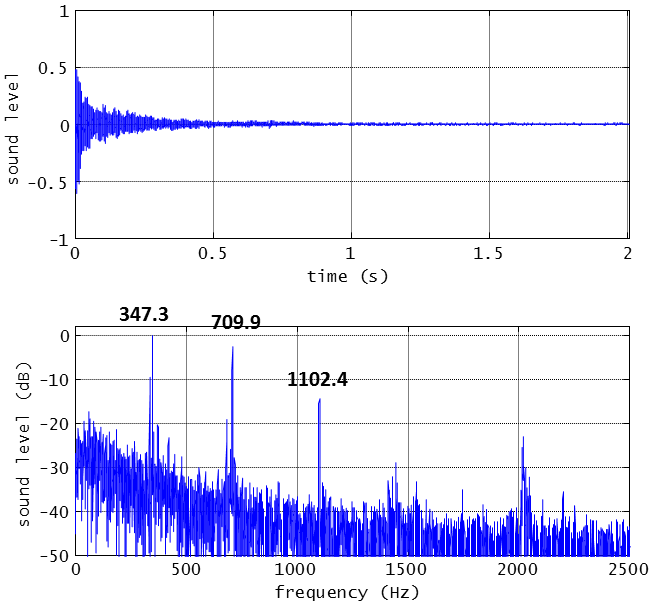
次の時間波形は、マイクロフォンが捉えた音圧変化です。

• 図の上段・・・音圧の時間波形
• 図の下段・・・時間波形をフーリェ変換して周波数軸上で相対パワー表示したもの(スペクトル波形)

上段の時間波形の中には、いろいろな周波数の音が入っています。

これを周波数軸上に変換して示したのが下段のスペクトル波形で、これを見ると、347.3 Hzというのがあります。1.8mm径のステンレス・スポークのテンションに対応するピッチ(音高)をこの347.3 Hzが支配しています。中央のF(ファ)に近い高さの音です。

ハンマーで打撃したときの音の高さとして、人はコレの周波数を認識します。どうやら打撃音はスポークテンション推定に使えそうですね。

しかし、次の山が710Hzです。これがかなりの曲者。347.3 Hzの整数倍になっていません。次の1102.7 Hzも同様です。

楽器が奏でる楽音は普通、基本次数の周波数に対して、整数倍の高次成分がズラリと並ぶことで、雑音ではなく楽音として成り立っています。

ところがスポークの打撃音は、雑味が強く、弦による楽音、というにはかなり質が悪い。

スポークの弦を打撃して得られる音は、ギター弦を爪弾いて倍音がキレイに見られるような状況とは異なる、ということになります。

やはり、特有の拘束状態が影響しているのでしょうか。自転車大好きな少年少女の方々の夏休みの自由研究の着目ポイントとして、ココは外せません。

ちなみに、次のスペクトル波形は、アルトリコーダーのA音(ラの音)です。基本次数の周波数が449 Hzで、その整数倍音がキレイにズラリと並んでいます。
　

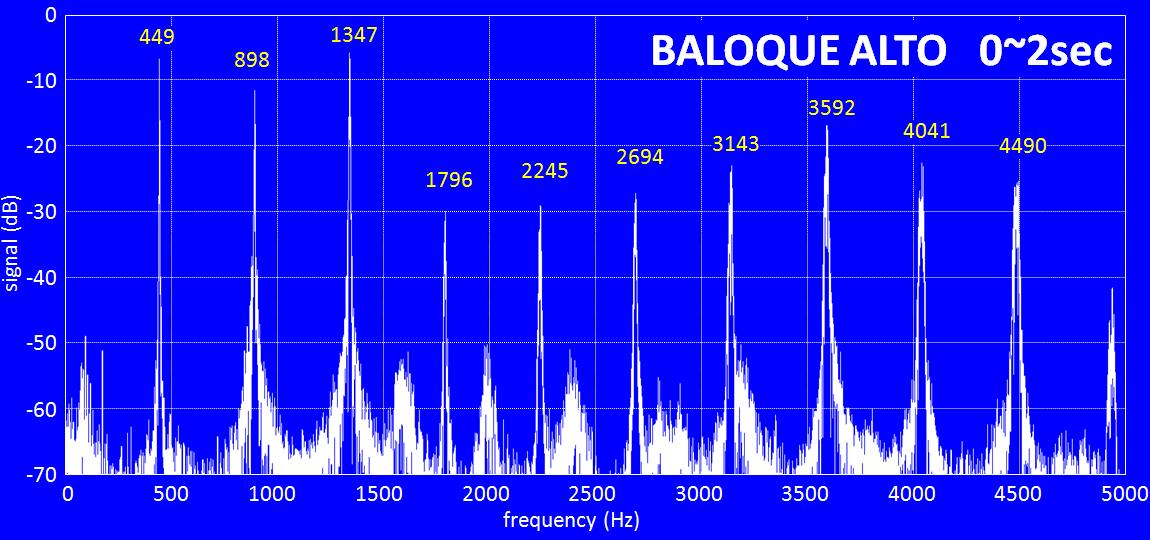
「あれぇ、Aが440 Hzじゃないのはなぜ?」

そうですよねぇ。これは昔、真夏の暑い日、エアコンも稼働していない部屋で、汗ダラダラで録音した音なんです。で、音速が温度で変化するので、管楽器の音高は相応の変化を示してしまうんです。音速Vは、気温をT℃とすると、

つまり、リコーダーの管長は変わらないのに、音速が速くなっちゃうんで、共鳴周波数が高くなってしまうんです。

というわけで、管楽器のピッチって、気温で変わってしまう。だからこそ、オーケストラは演奏開始直前にオーボエのA音でピッチ合わせをしてますよね。

ところが、どうやら欧州系のピッチはそもそも高めらしい。あちらのホールは暑いんですかね? ま、いいか。

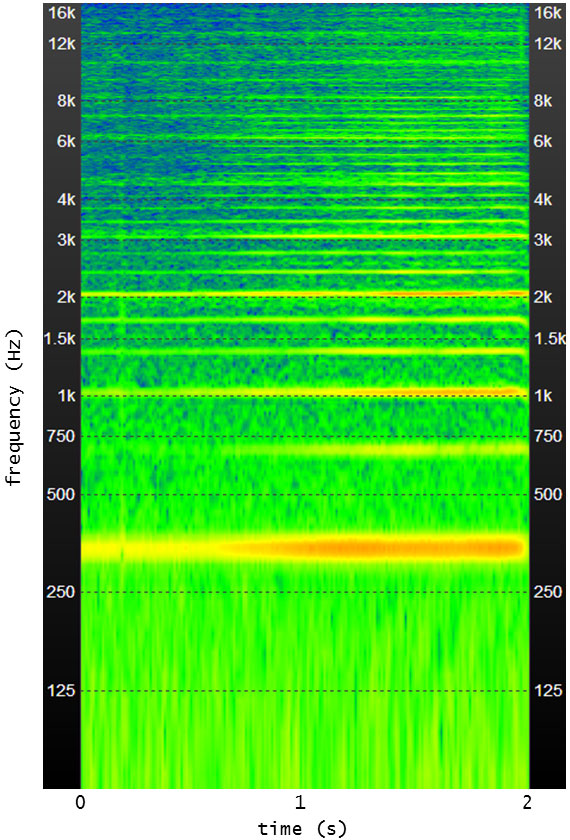
スペクトログラム

先ほどのスペクトル波形は、時間波形全てをまとめてフーリェ変換処理して周波数特性に変換したものです。

で、今度はスペクトログラム。これは、時間波形を短時間で細切れに区切ってフーリェ変換を施し、スペクトルが時間とともにどのように推移するのかを示したものです。

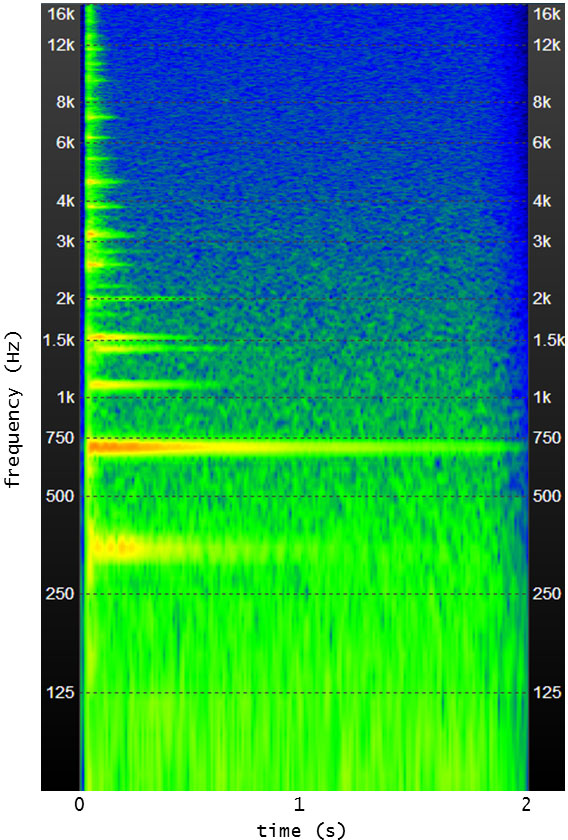
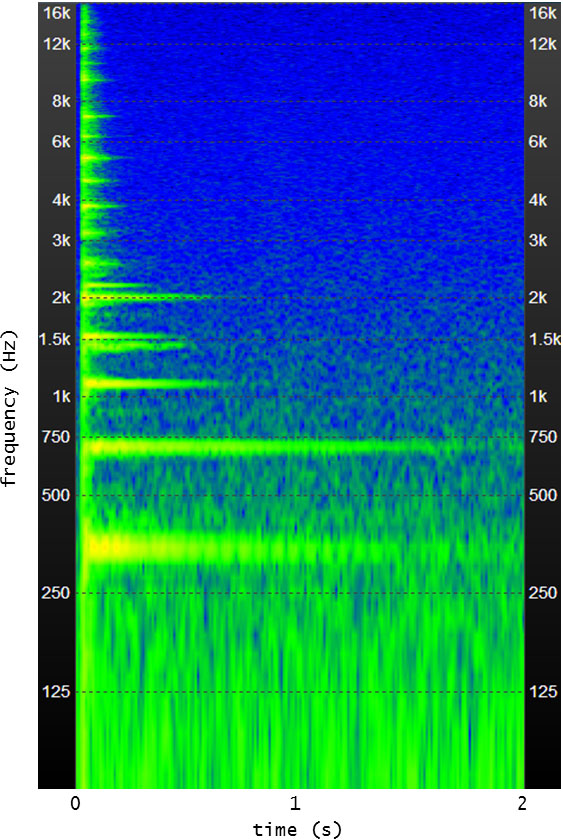
次の画像がそれ。スペクトログラムはフリーソフト ”SoundEngineFree” で簡単に得られます。おそるべしフリーソフト。まったくいい時代になったものです。

横軸が時間、縦軸が周波数、色が濃いところが、音圧が大きいところです。

これによると、困ったことに雑味成分の710Hzが長く鳴り続けています。周波数が高い上の方の成分も雑味満載です。スポークの打撃音が今一つ所在不明の煮え切らない音に聞こえていた理由はコレでしょう。

「所在不明の煮え切らない音」

この長年のモヤモヤがこれで一気に解けたような気がします。

なお、打撃に使うハンマーは小さいプラハンで、ヘッドに2mm厚ほどの牛革を貼り付けています。なるべくスポークのみの音を励起させるための策ですが、生のプラハンで叩くよりは、分かりやすい音になります。

プラハンでスポークを叩いているのですが実は、リムも、お付き合いで多少、鳴ってしまいます。

弦振動としては、大抵の場合、必ず基本的な弦振動成分が励起されますが、叩く、というパルス的な入力は非常に広い範囲の周波数を含むため、あらゆるものを鳴らす能力を持ちます。

このため、リム側の振動も多少、励起されてしまうようです。これも音高認識を邪魔しているようではあります。

爪弾きによる発音

スポークを爪で弾いてみたらどうでしょうか。

マイクロフォンが捉えた音圧変化を時間波形で見るとこんな感じ。

• 図の上段・・・音圧の時間波形
• 図の下段・・・時間波形をフーリェ変換して周波数軸上で相対パワー表示したもの(スペクトル波形)

ハンマリングと似たようなものですね。やはり、上の周波数と下の周波数の関係が倍音になっていません。

ほんの少しですが、ハンマリングよりも爪弾きのほうがわかりやすいかな?という気はしますが、濁っています。弦楽器のような心地よい音は、出ません。

次がスペクトログラム。347.3Hzが少し頑張っている感じ。ハンマリングより多少わかりやすいのはこれが原因でしょうか。

ヴァイオリンの弓による発音

ギターやベースに長年親しんでおられるというCBNレビュワーlandscapeさんによる4年ほど前のご投稿。

このYouTube映像の中で、Movistarの選手が弓弾でスポークから音を出している(ように見える)シーンがあるのですが、

これ、本当に弓で弾いて音が出ているのか！？

ということが話題になったことがあります。

もう四半世紀以上も昔の話ですが、ヴァイオリンの弓でスポークをそれらしく鳴らすことができる、ということを全く偶然、経験していたので(何やってんだ?)、私は図らずも答えを知っていたのですが、経験していなかったら、鳴るわけがない！ と思ったかも知れません。

さてその音とは・・・

Movistarオーケストラの弓弾き音よりも遥かにヴァイオリン的な発音です。

あれぇ～、こんな音だったっけ?? 超久しぶりの音出しに、自分が驚いてしまいました。この何ともたどたどしい音が、尤もらしさを演出します

・・・というか、まさかこの期に及んで再びヴァイオリンの弓でスポークを鳴らすことになるとは、感無量です。(※弓は当時、「おおーっ、スポーク鳴るじゃーん！」と喜んだ知人からタダで貰ったものです(安物らしい))

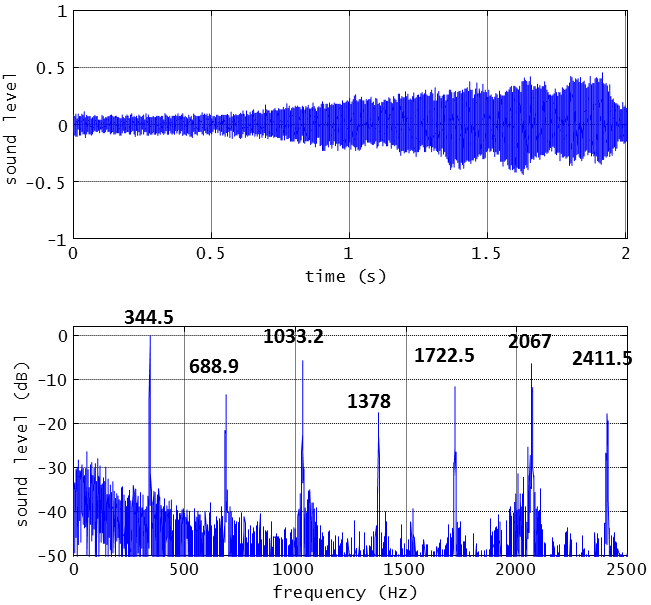
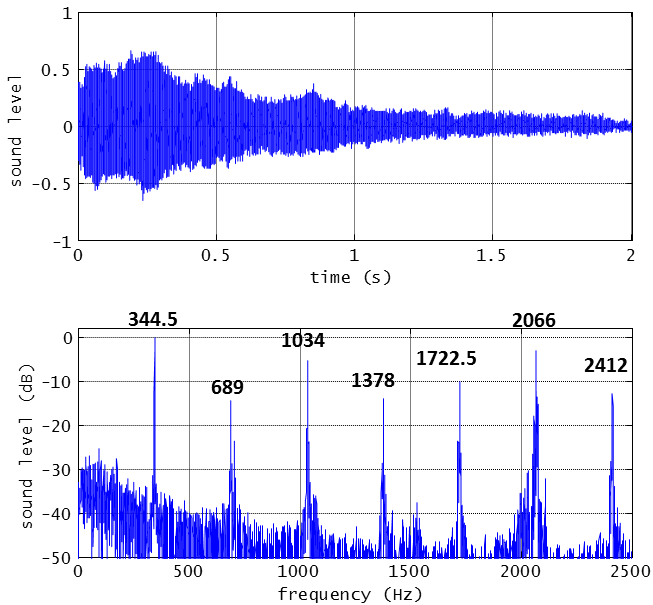
マイクロフォンが捉えた音圧変化を時間波形で見るとこんな感じ。

まず、弓を引いて発音させた場合。

次が押して発音させた場合。

まさしくこれは弦楽器の音。ずらりとキレイに倍音が並んでいます。楽音です。ハンマリングや爪弾きの雑味たっぷりのあの音は一体、どこへ消えてしまったのでしょうか？？

ヴァイオリンやウッドベースならば弓弾でもピツィカート（指弾き）でも倍音が並びますが、スポークは拘束状態が尋常ではないので、爪弾きやハンマリングでは倍音が並ばない。

ところが、弓を使うことで強引に、というか安定に倍音を励起することができるようです。これは驚愕の事態。もしかして、

『発見』

かも知れません。

いずれにしても弓弾による音の安定感は爪弾きやハンマリングとは全然別物、雲泥の差です。

馬毛の弓はまるで、魔法の杖。自然放出で光っていたLEDが誘電体単結晶の共振器構造を得て誘導放出を刺激され、レーザ発振を呼び起こしたかのようなありさまです。目覚めた！という感じ。

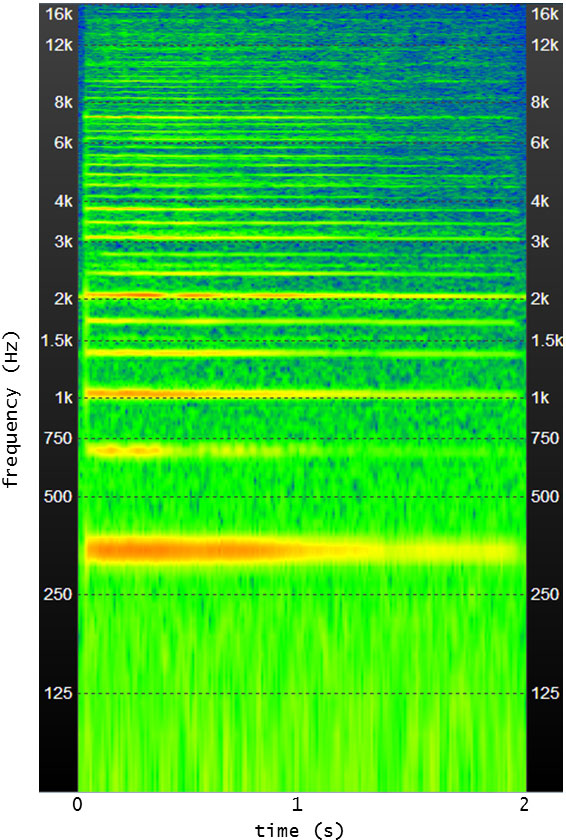
スペクトログラムを示します。ずーっと上の周波数までずらりと倍音が並んでいます。最初が引き側、次が押し側の発音です。

なぜ弓弾きだとこうなるのでしょう。

素晴らしすぎます。夏休みの自由研究でココは着目すべきポイントです、じゃなくて、これは一体どういうことでしょうか？大学などでの研究に値するテーマだと思いますが、如何でしょうか。

なお、ヴァイオリンの弓の毛には専用の松やにを塗布してスポークとの間に大きな摩擦抵抗を与えないと、到底、音など出ないのですが、あったはずの松やにが発見できず、やむを得ず次善の策として、毛に水をたっぷりとしたたるほどに染み込ませて音を出しています。

後日、松やにを入手してやってみましたが、何と、水作戦の時と似たような音しか出ませんでした。水の威力にも感嘆。

松やに・・・のどの痛みには効きません

6本組(3クロス)と疑似ラジアル組の音高の違い

フレットレス楽器のヴァイオリンは、弦を指で軽く抑えるだけで、その点を振動の節とすることが可能で、弦の長さを短くすることができ、相応の高い音を得ることができます。

一方で、交差組ホイールのスポーク。先ほど図で示したように2本のスポークが強烈に接触しています。ここが完全な節になるかどうかはわかりませんが、ラジアル組のスポークよりも音高が高くなるはずです。

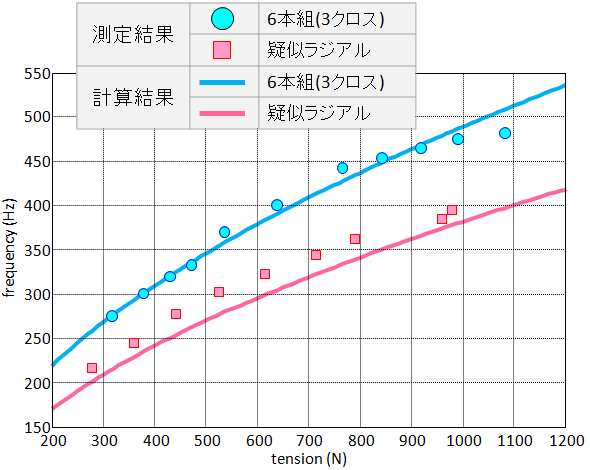
スポークテンションと音高の関係をグラフ化すると、次のようになりました。

縦軸の周波数は、弓引きで発音される基本次数の周波数、横軸のテンションはParkToolのTM-1で計測した値を採用しています。なお、TM-1の計測値が真値にどの程度近いのかは不明、です。

丸印や四角印が実測結果、実線は理論計算結果です。

ズレはTM-1の計測精度や、ステンレスの物性値の正確さ、そもそもスポークの終端固定条件がヴァイオリン弦のそれとはかなり違うなどなど、様々な要因が考えられますが、

単純な弦振動の理論式に実測値がこんなにうまく乗ってしまうのか！

が私の正直な感想です。ヴァイオリンの弓による発音と奏者、じゃなくて自転車整備者の絶対音感があれば、的確なテンション管理を行うことは可能、ということです。弓による音高は、最低次数のモードで発音する限り、極めて安定しているため、この意味で、

テンション計測器としての精度は、絶対値校正が完了していれば、通常の計測器よりも良いものになる

でしょう。

ところで、この図で、テンションは300Nから1100Nあたりで計測しましたが、頑張ってこれだけテンションを変えても、残念ながら音高は1オクターブも変化しませんので、この『弦楽器』で様々な音楽を奏でるのはちょっと厳しいようです。

それに指で押さえて弦振動の節を形成できるほどスポークはヤワではないので、なおさら、です。

しかし、せっかくスポーク音を収録することが出来たのですから、コレを素に、音階を作成して簡単な曲を作成してみるのも面白いでしょう。

結論

• スポークはヴァイオリンの弓で発音させることができる
• その音高は弦楽器の発音のように倍音成分に富み、イレギュラーな成分がない
• 弓弾きの音高はスポークテンションに精度よく対応するため、高精度なスポークテンション管理に使うことが可能である
• 一方で、スポークを打撃したり爪弾いて得られる音は倍音成分が極端に乏しく、雑味が極めて多い

なお、ホイールの仕様は以下の通りです。

• 32H　6本組(3クロス)
• リム：Ambrosio NEMESIS 32H
• スポーク：DT-SWISS Champion 1.8
• タイヤ：Vittoria CORSA EVO CX
• ハブ：SHIMANO ULTEGRA HB-6700

(※TM-1について)
TM-1の計測値は、測るたびに多少、上下し、ばらつきを持ちます。これは計測する人の問題と、TM-1の作動軸周りの不安定なフリクション、という2つが原因となって発生していると思われます。

TM-1でスポークを挟むときにわずかでもスポークをスポーク軸周りに回転させるような動きを手がしてしまうと、それだけで指示値は変化します。

また、TM-1を握った手を開いて、スポークに計測テンションを与えるときに、手の開きが速いとスポークテンションは低めに出ます。

さらに、TM-1の軸周りにはフリクションが存在し、この値がTM-1の計測精度を大きく支配しています。

フリクションであるがゆえに、その値はそれほど安定なものではなく、計測毎に指示値がばらつく原因となっています。

(※TM-1の軸フリクションの影響)
次のレビューのfig.6を参照下さい

cbn Park Tool TM-1・・・構造と計測原理編

(※この記事はCBN本館過去レビューを加筆再構成したものです)