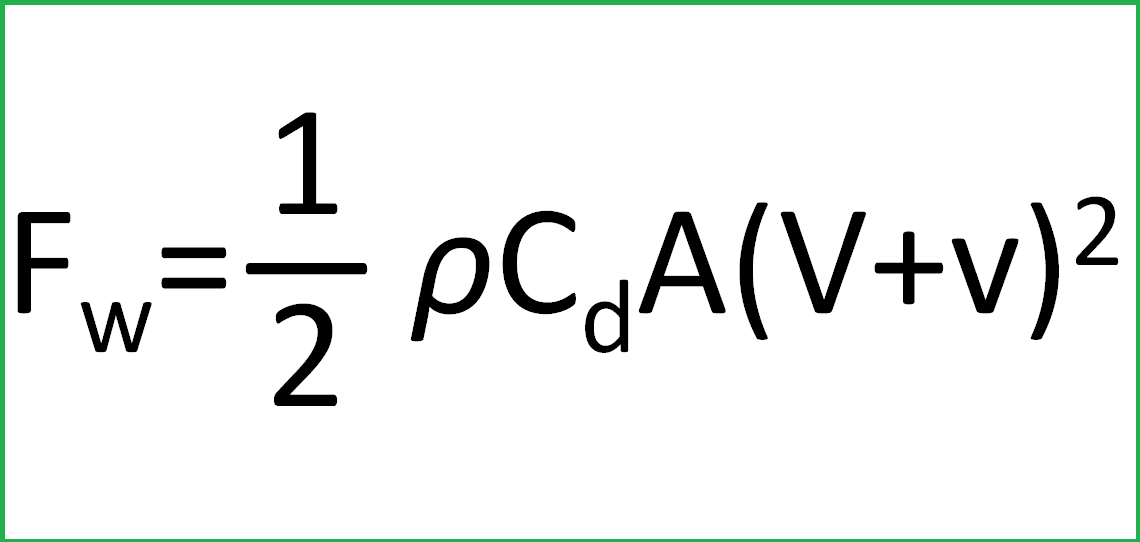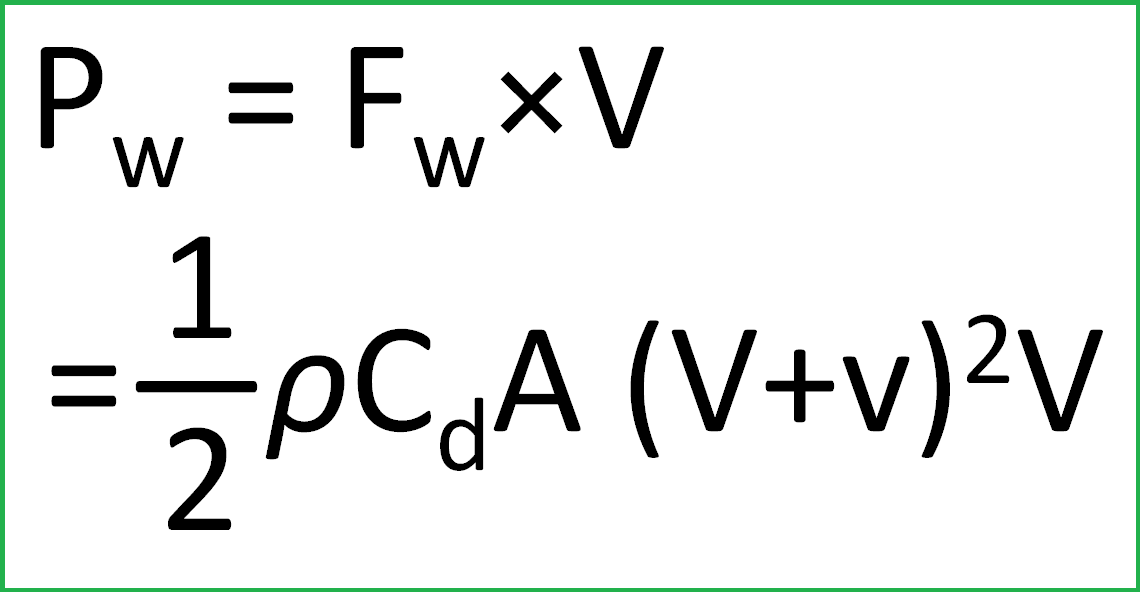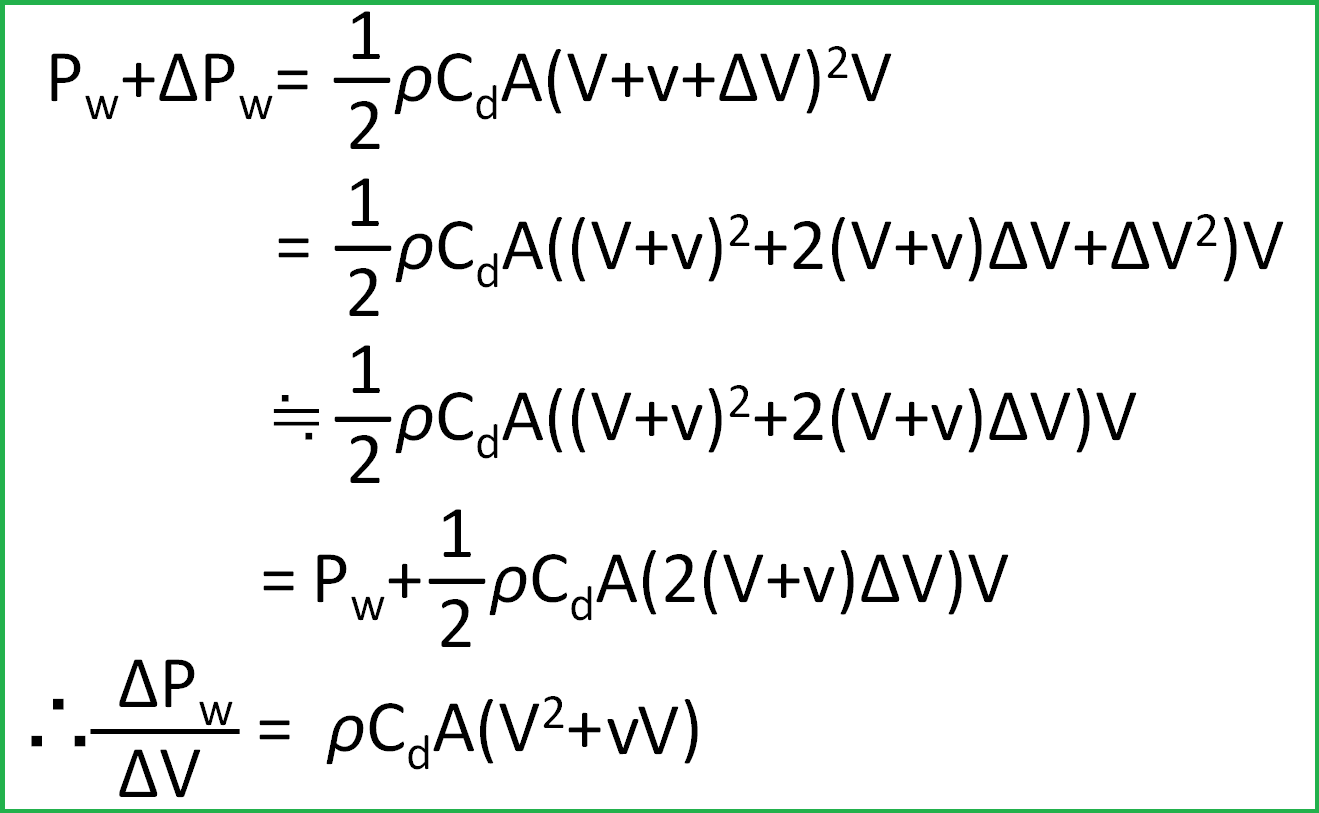日曜日の早朝。30kmほど快調に走ったところで、いつのもの平坦な直線に差し掛かった。
「よし、最高速度チャレンジだゼ！」
下ハンを握り、腰をわずかに浮かせて重心を前に移動し、強烈な引き足で回転を一気に上げていく。
「おおっ？今日は調子いいぜ！！」
これまでの実績では57km/h前後だった最高速度だが、今朝はついに、60km/hに達した。
「き、キター！！」
・・・
「少し追い風が吹いてたんじゃない？」
ある日、廃品回収業を営む屈強のスプリンター、尊敬するAさんに指摘されたのだが、まあそういえば、すこし追い風だったかも知れない。だが、多少の追い風でそんなに最高速度に影響するのか？う～む、釈然としない。
・・・
爆弾低気圧で風速15m/sのコンスタントな向かい風というのは、シャレになりませんが、穏やかな追い風は気分がいいですよね。春の南風に乗って都心から北関東の田園地帯に向かって楽々150kmほど走り、帰りは在来線でのんびり輪行・・・やってみたいなぁ～。
それにしても空力抵抗。走行速度が上がると容赦なく増大するような気がしますが、一体、どうなってるんですかねぇ？
「そんなの、わかりきったことじゃないか！」
まあ、それはそうなんですが、そんな当たり前のことを、少し真面目に考えてみます。
乗り手のパワーのゆくえ
乗り手は、ペダルを通して自転車にパワーを与えています。この、乗り手が自転車に与えたパワーのゆくえは一体、何処なのでしょうか？自転車のパワーバランスを示す、「パワーバランスグラフ」で見てみましょう。
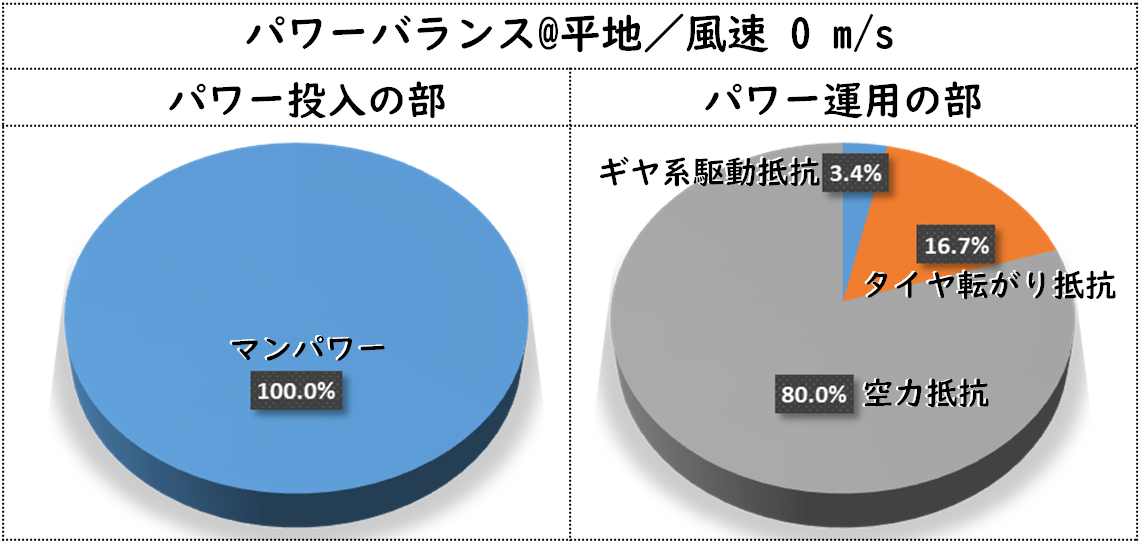
ひとつの例を挙げます。次の表は、平地無風の良路で、乗り手が250Wをロード自転車に投入した場合の、マンパワーの行先の計算結果です。乗り手は170cmで体重が66kg、自転車と合わせて74kgの質量を想定しています。タイヤの転がり抵抗係数は0.0058です。
また、この時の車速は、35.6km/hです。なお、道路勾配はゼロとしており、登坂抵抗もゼロとなりますので、登坂抵抗は計上していません。さらに、加速していない定常状態を扱うので、加速抵抗も計上していません。
この事例では、乗り手が発生したパワーが自転車に投入されるパワーのすべてなので、パワー投入を示す左側の円はその100%が、マンパワーとなっています。右側の円は、投入されたパワーの運用先です。
乗り手が250Wを出力した場合のパワーバランスグラフ → 車速35.6km/h
35.6km/hという速度領域で、すでに、空力抵抗の比率が80%に達しています。
このパワーバランスグラフの左円には、パワー投入の部として、マンパワーの250Wだけが計上され、これが100%を占めます。一方、右側には、パワー運用の部として、250Wの行先として5つの抵抗による消費パワーが計上されます。
この5つの抵抗というのは、
- ギヤ系駆動抵抗
- タイヤ転がり抵抗
- 空力抵抗
- 登坂抵抗
- 加速抵抗
です。ただし今回は、登坂勾配がゼロで、加速も考えないので、4番目と5番目の抵抗は省略しています。
抵抗の科目は、細分化しようと思えば、いくらでも細分化できますが、自転車という乗り物のパワーバランスをわかりやすく理解するためには、まず、この5つに着目することが重要です。
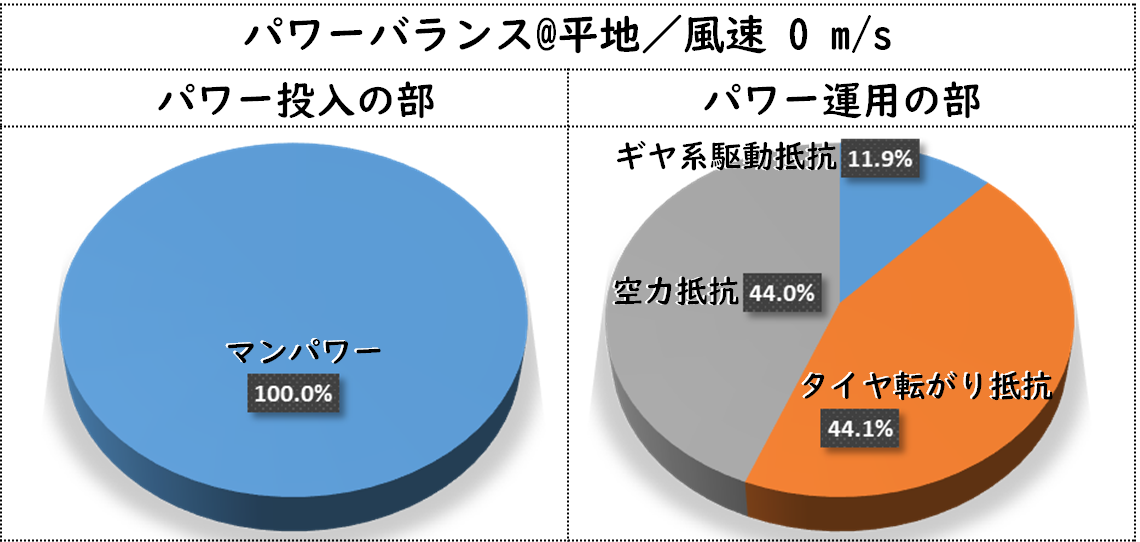
ちなみに、16km/h前後というポタリング速度まで車速を落とすと、ようやくタイヤ転がり抵抗と空力抵抗が拮抗します。それが次のグラフですが、この時のマンパワーはわずか43Wです。
乗り手が43Wを出力した場合のパワーバランスグラフ → 車速16.2km/h
ロード自転車の場合、タイヤの転がり抵抗と空力抵抗が拮抗するのは16km/h付近という低速ですが、一方、自動車の場合は、この拮抗速度が60km/h程度となります。
クルマのタイヤの転がり抵抗係数がロードタイヤより劣るというのも拮抗速度が大きくなる理由の一つですが、自動車というのは空力特性が自転車より格段に優れている、というのが理由の大きな部分を占めます。というか、乗り手を含めた自転車の空力特性はクルマと比較すると、相当に劣悪、と言っても良いかも知れません。
おっと、さっそく脱線してしまいましたので本題へ復帰します。
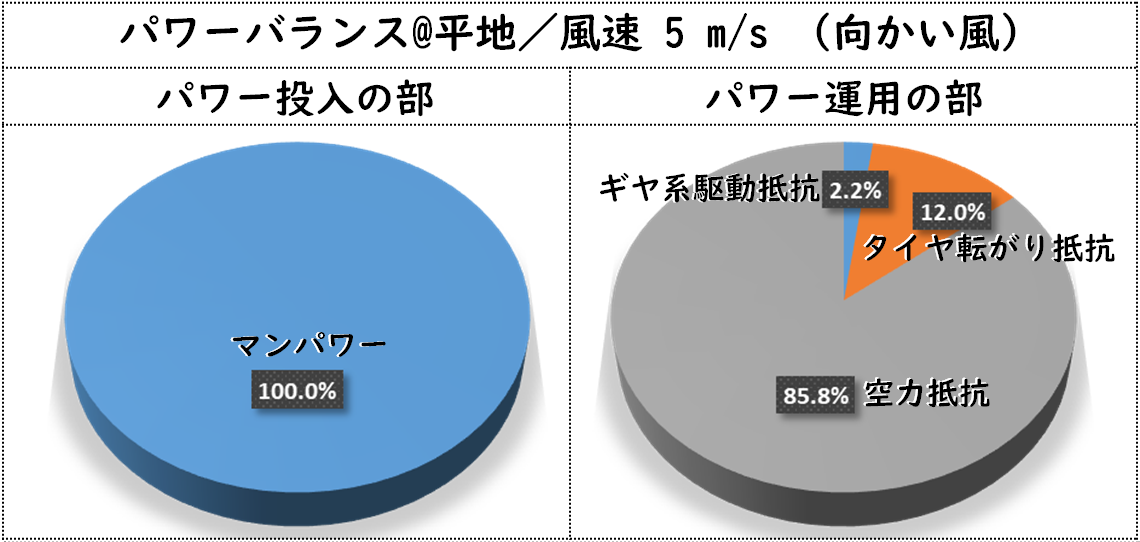
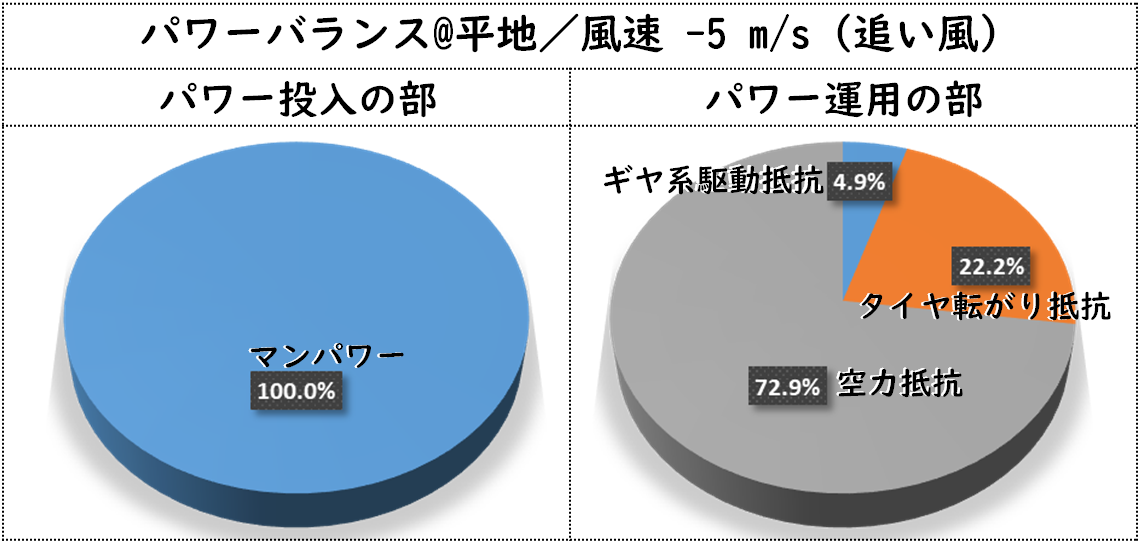
次のグラフは、向かい風5m/sの場合で、同じく250Wを投入した場合の、マンパワーの行き先を示します。
風速5m/s（向かい風）で、乗り手が250Wを出力した場合のパワーバランスグラフ → 車速25.6km/h
僅か（?）5m/sの向かい風で、車速が35.6km/hから25.6km/hまで落ち込みます。これはものすごいインパクト！車速が落ち込んだのに空力抵抗の割合が85.8%に上昇しています。さらに、次のグラフ。今度は追い風5m/sで同じく250Wを投入した場合の、マンパワーの行き先です。
風速-5m/s（追い風）で、乗り手が250Wを出力した場合のパワーバランスグラフ → 車速43.5km/h
僅か（?）5m/sの追い風向かい風で、車速が35.6km/hから43.5km/hまで上昇します。これまた強烈なインパクト！車速が増大したのに空力抵抗の割合が72.9%まで低下しています。
風速5m/sというのは、3.6倍して時速に換算すると、時速18km/hです。つまり、追い風5m/sのもとでは、風速ゼロの場合の車速35.6km/hに18km/hを足して、時速53.6km/hで走ると、ようやく風速ゼロの場合と同じ空力抵抗を受けることになりますが、車速増大に比例して転がり抵抗も増大するので、時速53.6km/hに到達することはできず、43.5km/hという車速になっている、というわけです。
ひとつ前のグラフで示した向かい風の場合も同様で、向かい風5m/sのもとでは、風速ゼロの場合の車速35.6km/hに18km/hを引いて、時速17.6km/hで走ると、ようやく風速ゼロの場合と同じ空力抵抗を受けることになりますが、車速低下に比例して転がり抵抗も減少するので、時速17.6km/hまで低下することはなく、25.6km/hという車速になっている、というわけです。
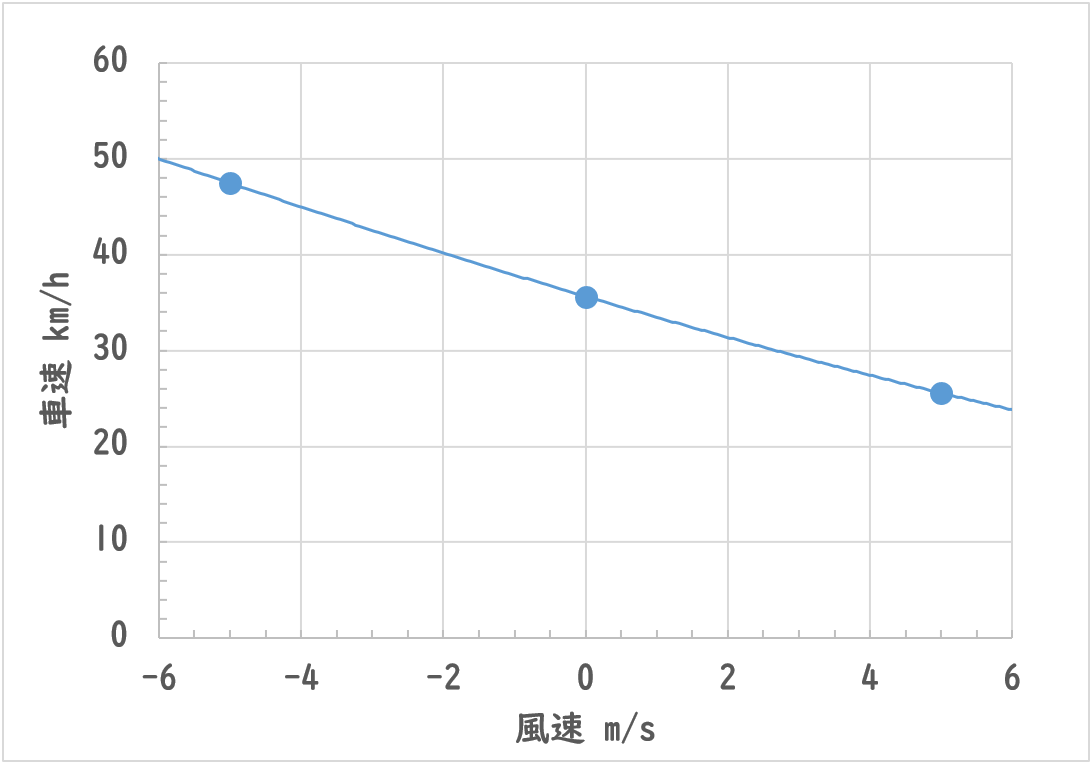
マンパワーが250Wの場合の、車速と風速の関係もグラフにしておきましょう。
乗り手が250Wを出力した場合の風速と車速の関係
な、何だって！？わずか風速1m/sの向かい風で車速が2km/hも落ちるってか。嘘だろ？？
今でこそパワーメーターが隆盛を極めていますが、元々、自転車乗りという類の人々は所詮、サイコンの車速を参照して、それを、ありたき車速と比較してその差分を埋めるべくパワーを調整する類の人々です。
つまり車速フィードバックで走ってしまうのが自転車乗りの性というもの。一方、ヒルクライムTTを心拍数基準で走る、という人はずいぶん前からいましたが、この方々は、パワーフィードバックで走る先駆者です。しかし、普段の走行場面でパワーフィードバックで走る人というのは、まだ少数でしょう。
そうなると、1m/sの向かい風で車速が低下していたとしても、それに気づかず、
う～ん、なんか調子が出ないぜ！
と考えて少しパワーを上げて走ってしまうことになります。その積み重ねが、微風なら車速にほとんど影響しない、という思い込みを醸成します。（かなり独断的意見ですが！）
空力抵抗はどこからやってくるのか
空力抵抗はどこからやってくるのでしょうか。心当たりを探ってみます。
空気
空気は窒素が8割近く、酸素が2割ほどを占める気体で、重さがあります。単位体積当たりの質量を「密度」というのですが、20℃で1気圧の大気圧における乾燥空気の密度ρは、
ρ= 1.205 kg/m^3
つまり、1立方メートル当たり1.205 kgです。結構重いですよねぇ。自転車はこの空気をかき分けて走るのですから、密度ρが大きいほど、抵抗が大きくなるということが想像されます。
ちなみに、この数値が海抜0mでの空気密度だとすると、標高2000mでは空気が薄いので、 ρ= 0.959 kg/m^3 まで小さくなります。海抜0mの5%下り勾配で惰性走行して最終的に44km/hに到達するような場合、同じことを2000mの高地でやると、到達速度は49km/h程度まで上昇することでしょう。
欧州レースで、山岳の下り速度が尋常ではないのは、こういうことも理由の一つとなっているのではないかと考えられます。
面積
自転車で走る姿を前方から振り返ってみると、こんな感じですよね。ここから前面投影面積Aを定義することができます。この面積Aが大きいほど、風の影響を強く受けますから、空力抵抗も大きくなるということが想像されます。ちなみに、身長170cm、体重66 kgであれば、ロード乗車の場合の前面投影面積は0.4 m^2 程度となるようです。
前方正面から見込んだ黒塗り部の面積が『前面投影面積』
形状
前方から見込んだ面積は上の図ですが、この人が奥行き方向にペラっペラなのか、それとも奥行きがあるのか、はたまた、ビョ～ンと翼断面のような形を具備している人なのか？・・・それがつまり、形状です。
この形状の良し悪しを、「空力抵抗係数」という便利なモノで表します。Cdってやつ。クルマ好きな方の中には、「4代目プリウスは驚異のCd値0.24」 とか、数字を知っていたりする人がいたりして驚いてしまいますが、ソレです。
Cdというのは係数なので無次元（単位なし）です。（実はCdというのは気体の粘性や気体流れの速さなどにも依存して決まる量なので、単純な説明をしてしまうとあまりよろしくないのですが、本稿では省略します）
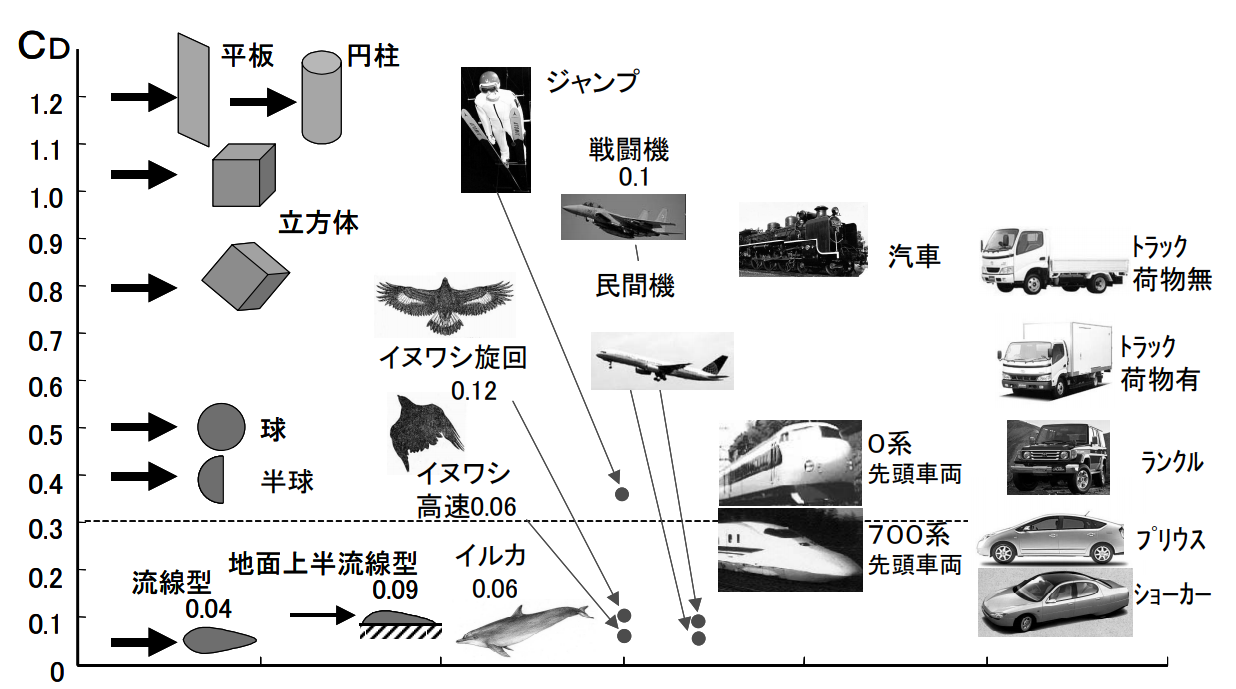
面白いCd分布図をご紹介します。これは一般社団法人日本流体力学会の学会誌 『ながれ』 の2004年第6号に掲載された『自動車と流体力学：車体周り流れと空力特性』の図8からの引用です。なんだか妄想しちゃいますねぇ。
ちなみに、身長170cm、体重66 kgであれば、ロード乗車の場合の空力抵抗係数Cdは0.9程度となるようです。空荷トラックと同等！？
車速
車速Vが大きくなるとそれだけ空気を余計にかき分けますから、空力抵抗が大きくなるでしょう。ちょっと当たり前すぎますが、車速Vもここに挙げておきましょう。
風速
最後に風速。向かい風vが大きくなると、それは車速に上乗せされますから、空力抵抗がさらに大きくなるでしょう。風速vも忘れずに挙げておきましょう。
空力抵抗は『 車速 + 風速 』の2乗に比例して増大する
さてさて、役者が揃いました。五役揃い踏み。
- 空気密度ρ (kg/m^3)
- 前面投影面積A (m^2)
- 空力抵抗係数Cd
- 車速V (m/s)
- 風速v (m/s)
これらを使って、空力抵抗という力の大きさFwを表す式は次のようになります。五役が参列してますねぇ。速度と風速のカッコ部分が2乗ですが、そこに気を付けて上記五役の単位をこの式に当てはめると、 kg m/s^2 となります。実はコレ、力（蚊じゃなくて、ちから）の単位でN （ニュートン）と同じものなんです。
空力抵抗という力の大きさFwを表す式
というわけで、
空力抵抗という力の大きさは 『 車速 + 風速 』 の2乗に比例して増大する
ということになります。無風状態で車速Vの場合は、乗り手が受ける風速も同じVということになりますが、無風でないとすれば、車速と風速の和 V + v が、乗り手が受ける風速となります。
ところで、
この式の1/2って、いったい何？
なーんて疑問に感じてしまう方。ホント、そうですよねぇ。これを説明するのはちょっと本稿の範囲を越えるので省略しますが、興味を持たれた方は是非、調べてみてください。高校生の方なら、物理の先生に質問しても良いでしょう。
さらに、
おかしいなあ、高校の物理では、空力抵抗の力は速度の1乗に比例するって教わったような気がするんだけどなあ
というのは私の記憶です。あれは一体、何だったのか？
空力抵抗には、速度の1乗に比例する「粘性抵抗」と、速度の2乗に比例する「慣性抵抗」が存在するとされています。
空気などの流体中において、粘性抵抗と慣性抵抗のどちらが支配的になるかを決定するのがレイノルズ数と呼ばれるもので、これは流体の密度と粘性、運動体の速度と長さで表される数です。このレイノルズ数が小さい場合、粘性抵抗支配となり、速度に比例する空力抵抗が運動体に作用します。
反対に、レイノルズ数が大きい場合には、慣性抵抗支配となって、運動体に速度の2乗に比例する空力抵抗が作用します。まあ、正直に申し上げて、普通の形をした物体に速度の1乗に比例した空力抵抗が作用する速度範囲は非常に狭く、高校の物理の時間に実験で示すのは極めて難しいでしょう。
それでも速度の1乗に比例すると教えていたのは、2乗としてしまうと運動方程式を高校の数学で解くのが難しくなるからですかねぇ？？
自転車の場合、サイコンに速度が表示されないような超低速の領域でも、すでに速度の2乗に比例する慣性抵抗が優位になるため、全速度域で慣性抵抗支配と考えて全く差し支えありません。
レイノルズ数というおまじないのような言葉に興味を持たれた方は、これも是非、調べてみてください。高校生の方なら、もちろん、物理の先生に質問しても良いでしょう。
どうして空力抵抗は速度の3乗に比例するのか
注意していただきたいのは、空力抵抗の単位。元々、本稿では、コレをパワーとして扱っており、単位はW（ワット）なのですが、先ほどは、空力抵抗を力Fwとして定義していました。
パワーとは力×速度である
というのはcbnblogで度々登場している話ですが、これは結局、『空力抵抗という力Fwに車速Vを掛ければパワー Pwになる』ということを示しています。つまり、車速Vと向かい風vの場合は、
空力抵抗というパワーの大きさPwを表す式
無風、つまり v=0 とすると、この式に車速Vの3乗の項がくっきり表れます。そんなわけで、「空力抵抗パワーは速度の3乗に比例する」というわけです。さて、無風状態で、車速30km/hを基準速度として、車速を5km/h刻みで上下させた場合に、空力抵抗パワーPwが何倍に変化するでしょうか？
上の式でv = 0 として計算すると、こんな風になります。
- 車速15km/h → 0.125倍
- 車速20km/h → 0.296倍
- 車速25km/h → 0.579倍
- 車速30km/h → 1倍
- 車速35km/h → 1.588倍
- 車速40km/h → 2.370倍
- 車速45km/h → 3.375倍
車速を30km/hから40km/hに上げると、空力抵抗パワーは実に2.37倍になります。
ほんの少しだけ速度を上げると・・・?
先ほどの空力抵抗パワーPwの式で、車速Vがほんの少し、ΔVだけ大きくなったとすると、空力抵抗パワーPwもほんの少し、ΔPwだけ大きくなるでしょう。その、ほんの少しのΔPwって、どういう 『ほんの少し』 なのでしょうか。
次の最後の式で示されるΔPw/ΔVというのは、ほんの少しだけ速度を上げたときに、どのくらいほんの少しPwが増加するか、ということを意味します。簡単に言うと、車速を1km/hだけ上げると、空力パワーはどのくらい増加するのか？というような、『感度』を表していることになります。
車速増加ΔVに対する空力パワー増加ΔPwの感度を示す式
少々面倒ですが、風速vをゼロとして最後の式を眺めると、
ほんの少しだけ車速を上げたときの空力抵抗パワー増加へのインパクトは、その時の車速の2乗に比例する
ということがわかります。風速vが存在すると、そのインパクトがさらにv×V分だけ上乗せされます。
例えば、無風時に、車速30km/hから+1km/hだけ上げる場合と、車速40km/hから+1km/hだけ上げる場合とでは、空力パワー増加へのインパクトは 40/30 の2乗倍だけの違いがある、ということになります。つまり、1.78倍です。
車速が高速域になればなるほど、そこからわずか1km/hだけ速度を上げるのがどんどん辛くなる、ということを示しています。ちょっとした式のお遊びですが、上の一連の式は高校で教わる 『微分』 という操作に相当します。
ところで世界レベルのトラック・スプリントの世界。今シーズン、ワールドカップで活躍をみせる競輪の深谷知広選手が12月8日、ニュージーランドでのワールドカップ第4戦のスプリントでついに銀メダルを獲得しましたが、その予選の200mフライングTTで何と9秒609をたたき出しました。
つまり74.93km/hですよ！深谷選手、凄すぎ！！ 70km/hオーバーの世界では、+1km/h毎に競技レベルが異なるといっても良いくらいの異次元ワールドでしょう。ノーマルな競輪マシンでは到底、到達不可能なスピードですが、ブリヂストン製のトラックマシンの空力特性の良さも影響しているのではないでしょうか。
耐久ランの走行時間
耐久ランなどと呼ばれる行為。すでに40年ほど前の自転車雑誌で、主要耐久ランの参考タイム一覧のようなものを見た記憶（かなり怪しい記憶）があるのですが、古の時代から自転車乗りは長い距離を走ってその走行時間を自分の走行記録簿に書き留める、という行為を繰り返してきました。よく知られるのが日本橋～直江津とか、日本橋～大阪とか。
ここまで読んでいただいた読者の方はすでにお気づきだと思います。耐久ランに要する時間は、わずかな風によって大きな影響を受けるはずである、ということを。
もし同じパワーで走り続けたとすると、追い風1m/sと向かい風1m/sでもそのタイムには大きな差が生まれます。追い風1m/sで600kmの距離を車速30km/hでノンストップで20時間をかけて走り切った（信号で数えきれないくらいの回数、止まりますからノンストップなんてありえませんが）とすれば、その際のマンパワーを使って今度は向かい風1m/sの元で挑戦すれば、23時間以上を要することになります。
前述したとおり、自転車乗りはどちらかというと車速フィードバックで走りますから、向かい風では無意識にマンパワーを上げた走りになってしまうし、追い風ではマンパワーを絞り気味にしてしまうものですので、3時間以上といった大差はつかないことになるとは思いますが、いずれにしても風は全く侮れない、ということは本稿を通じて理解していただけたと思います。
まとめ
- 空力抵抗パワーは、無風であれば『 車速 』 の3乗に比例して増大する
- 平地良路で乗り手が250Wを出力して車速35.6km/h付近で走行する場合、空力抵抗パワーはマンパワーの80%程度を占める
- ほんの少しだけ車速を上げたときの空力抵抗パワー増加へのインパクトは、その時の車速の2乗に比例する
- 車速への風の影響は、全く侮れない
▼ 自転車の理論・科学・解析に興味がありますか？ 下のページでチェックしてみて下さい
