2019年1月号から版型が新しくなり、連載も様々に変化し続けるサイスポですが、たった一度の連載であっという間に消え去った連載「君は知っているか」など、出入りの激しい昨今の状況です。
石田ゆうすけ氏による珠玉の連載紀行「僕の細道」がある限り、サイスポは不滅ですし、特集記事はなかなか読ませる内容ですから、判型変更後のバタバタ感はむしろ、編集者たちの奮闘の現れなのでしょう。
そんな中、ほぼ毎月連載の鏑木裕氏「カブラボ(CUB-LAB)」が面白いです。あまり深入りせずに事象のエッセンスを伝えることに集中しているところは2ページ連載ならでは、と言うよりも、鏑木氏らしい、と思うわけであります。
というわけで6月号カブラボ(214,215ページ) のテーマ
ホイール重量はどれだけ速さに影響するの？
に勝手に連動！
![CYCLE SPORTS (サイクルスポーツ) 2019年 6月号 [雑誌]](https://images-fe.ssl-images-amazon.com/images/I/51nnLl5L1lL._SL160_.jpg)
カブラボ(CUB-LAB)とは
カブラボ(CUB-LAB)は、鏑木裕氏が主宰する自転車総合研究所で、
身近なモノと創意工夫で実験を行い、さらなるサイクリストの高みを目指すことを目的とした
研究所、とのことです。
「身近なモノと創意工夫で実験を行い」・・・にグッと来てしまいます。言葉遊びではなく、創意工夫こそ創造的で幸せな自転車ライフの源泉であると私など勝手に思っているわけですが、鏑木氏の姿勢には敬意を表するところです。
で、鏑木裕氏は少し前まで轍屋自転車店の店主さんでしたし、屈強なMTBライダーですし、かつてのサイスポ連載「ダートクエスト」などが思い出されますし、さらに遡ると、サイスポ編集者でした。鏑木氏の自由な生き方への志を感じてしまう昨今ですが、今後のご活躍に期待してしまいます。
サイスポ6月号のお題
そして6月号のカブラボ (214,215ページ)のお題は
ホイール重量はどれだけ速さに影響するの?
です。
鏑木氏の「寸止め」の妙味、その先は読者に委ねられている
しかし、鏑木氏はたった2ページの企画故なのかどうか、詳細にはあまり深入りせず、測定結果を端的に示し、その後の議論は読者に委ねているようにも見えます。測定結果を並べて、
やっぱりデュラエース、何よりチューブラーはすごいってコトだ！
と、結構な平板発言で締めくくっています。この言いっ放し感がいいじゃないですか。これはまさに、
「寸止めの妙」
あとは自分で考えなさい、と。
何事もキッパリ言ってくれる鏑木氏が有り難いのではなく、ちゃんと自分で考える余白を残してくれる鏑木氏に凄みを感じるわけです。
その先は自分で考える。他人ではなく自分のための答えは自分で見つける。それが間違っていたっていいじゃないか。声の大きい人とか権威筋の言説がいつも正しいなどと、努々、思うことなかれ、ということです。
しかし、もしかしたらサイスポ読者の大半は、この余白を埋めるなどという発想がそもそもないかもしれません。
また仮に、誌上で一から十まで手取り足取り丁寧に解説しても、それを正確に読み取って本質を理解するような作業は面倒だし、興味もない。上っ面の刺激的な言葉だけがすくい取られて流布され、それがやがて、都市伝説になる。（おいコラ、調子に乗って何言ってんだ）
ですから、今回のblog記事も随分と面倒に見えますし、面白くもないし、興味もないという方が大半だと思います。それでも、中には読んでくださる方も存在します。そういうマイノリティを私は大事にしたいと思っています。
実験結果
さて、今回のカブラボで提示された実験結果。実に素朴なセットアップで計測された数値であるということを考慮しなければならないでしょう。
高精度な計測を行えば多少、違った結果が得られたのかも知れませんが、それでは身近なものでサラリとやってのける鏑木氏の流儀には沿いません。
それが欲しいならそれこそ、自分でさらなる工夫を凝らして、やってみましょう。あ、いえいえ、今回はその方面には行かないでおきます。
今回の実験の趣旨は
ホイール重量はどれだけ速さに影響するのだろうか? これを理解したい
ということですが、カブラボで行われた実験方法はおおよそ、以下の通りです。
- タイヤ付きのリアホイールに11Tのスプロケだけを取り付ける
- ホイールを保持し、スプロケに架けたチェンに括りつけた3kgのダンベルの重さでホイールを回す
- ダンベルが90センチだけ落下するとチェンがスプロケから外れ、ホイールの加速が終了する
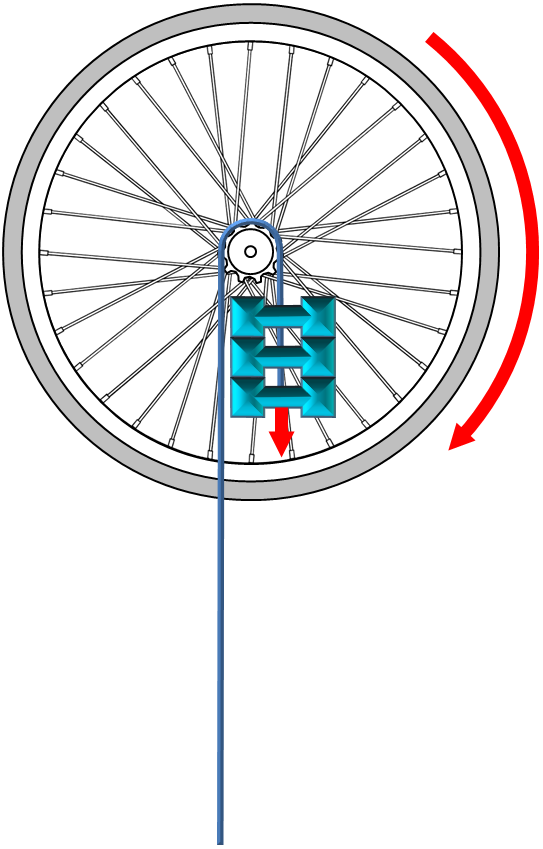
次の図も参照して実験方法を掴んでください。
サイスポ6月号カブラボ実験の風景はこんな感じ
ホイールを支える手を離すと、ダンベルが落下を開始し、ホイール回転速度が徐々に大きくなります。そして、チェンが90センチだけスプロケを駆動したところで離脱して、その後はホイールが空転して、徐々に速度を落としていきます。その結果は次の通り。
サイスポ6月号カブラボ実験の結果一覧
エントリー銘柄は、
- 軽量なデュラのホイール
WH-R9100-C40-TU - アルテグラ
WH-RS700-C30-TL - 廉価版
WH-RS100
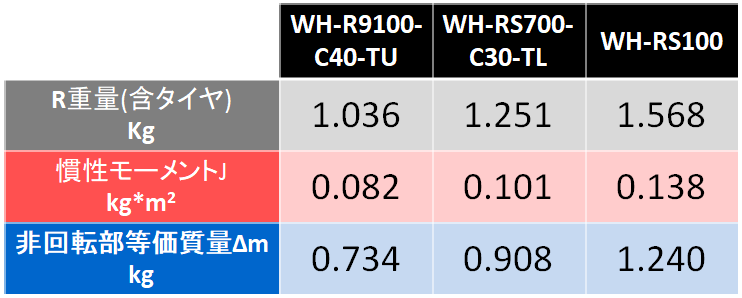
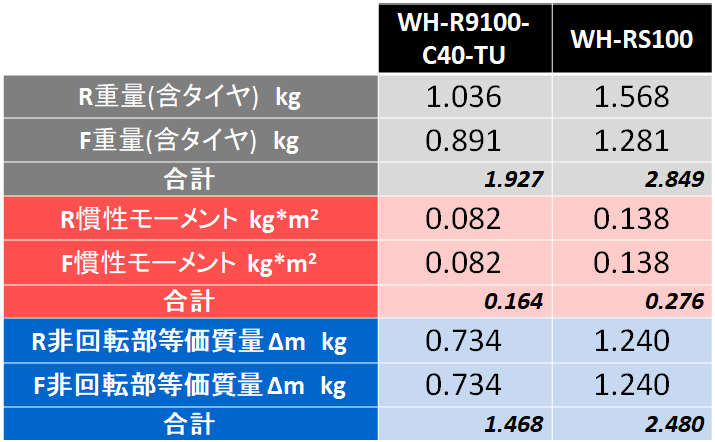
それぞれのリアホイールに相応のタイヤが装着され俎上に乗っています。御覧の表の通りで、タイヤも含めるとデュラR9100と廉価版RS100の重量には実に1.5倍程度の開きがあり、その差はリアだけで500g以上もあります。
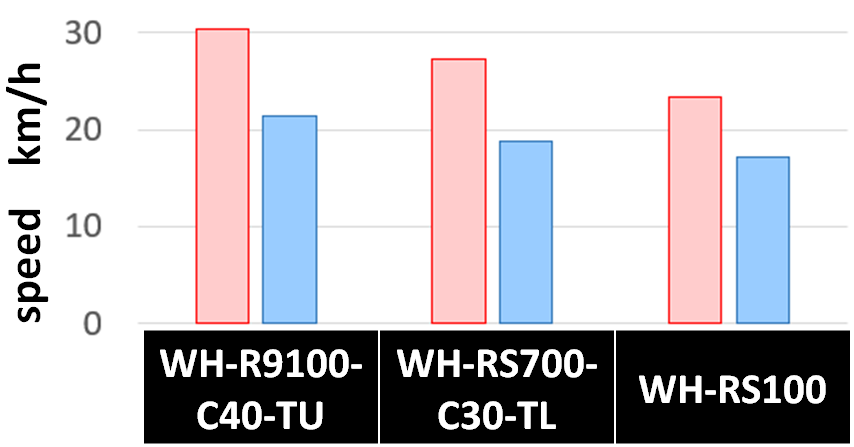
というわけでこの重量が効いたのか、最軽量のR9100の最高速度が30.3km/hまで到達していますが、重量が1.5倍もあるRS100は23.4km/hにとどまります。
ところが、空走30秒間の平均速度は、一気に差が縮まります。最軽量のR9100は最高速度と30秒空走平均速度の差が8.9km/hですが、最重量のRS100は同じく6.2km/hにとどまります。
まずこの表をパッと眺めてわかることは、
軽量ホイールは加速容易で減速も迅速、重量ホイールは加速ゆっくりで減速もゆっくり
です。表の数字をそのままグラフ化するともう少しわかりやすくなります。それぞれの銘柄で、赤棒が最高速度、青棒が空走30秒間平均速度。
サイスポ6月号カブラボ実験結果をグラフ化してみた
このグラフを
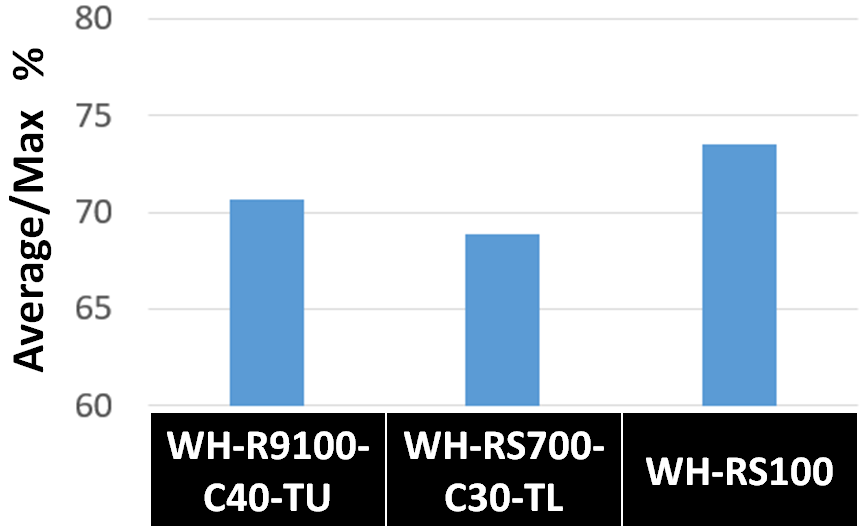
空走30秒間平均速度(Average)を最高速度(Max)で割った値
によって書き換えてみます。それが次のグラフ。
空走30秒間平均速度(Average)を最高速度(Max)で割った値のグラフ
慣性モーメントが小さく、加速しやすくて減速しやすいR9100の値が小さくなるのは理解できますが、RS700がさらに小さくなっています。つまり、RS700は空走時の減速が過剰に見えてしまうんですよね。
同じ軸まわりフリクション（空力も含めて）を想定すれば、重量に対するこのグラフの感度は単調増加になると思われますので、おやっ？と思わせる結果です。原因はいろいろ考えられますが、しかし実はこれが、
実験の醍醐味
でありましょう。妄想の迷路へと導くグラフです。
その先へ勝手に行ってみよう
さすがデュラR9100。加速ダッシュでRS100の自転車にこれだけの速度差をつけることができるなんて、スゴ過ぎるぜ!!
先ほどの実験結果を見て、こんな風に早合点する人はいないとは思いますが、この実験結果はホイール＋タイヤだけの結果であり、自転車が走った場合のものではありません。念のため。
さて、この実験では、何がどうなって、結果として何を示してくれているのでしょうか？ ちょっと冷静に考えてみましょう。
ダンベルの質量をm(kg)とします。h=0.9(m)の落差だけダンベルが降下するまで、チェンが11Tスプロケに架かってホイールを加速し続けます。hだけ降下した時点でのダンベル速度をv(m/s)、ホイールの慣性モーメントをJ(kg*m^2)とすると、
・・・(1)
これはつまり、
高さhにある質量mのダンベルが持つ位置エネルギー mgh でホイールを回したのだが、その結果、質量mのダンベルが速度vになり、同時に、慣性モーメントJのホイールの回転角速度がωになった
というわけで、
エネルギーmghが
と 
に配賦された
ということを示しています。
ただし、実際にはホイールの軸回り抵抗、つまり軸フリクションやスポークなどによる空力抵抗が消費するエネルギーの項、スプロケの左側から右側に刻々と入れ替わるチェンの質量に関する項も扱った方が良いのですが、ここでは大勢に大きく影響しないと考えて、議論を簡素化するために無視しています。
ところで慣性モーメントとは何者なのか
先ほどの式で、ホイール回転角速度ωなどというものがどこからともなくやってきています。大体、このωが何だかよくわからないですよねぇ。まず、コレから片付けます。
自転車が走っているときに、ホイールが勝手な速度で回るなどということはありません。つまり、
ホイールの回転速度は、車速で拘束されている
普通に走っていれば大体、そうですよねぇ。車速をV(m/s)、タイヤ実効周長から得られるタイヤ実効半径をR(m)、ホイールの回転角速度をω(rad/s)とすると、
・・・(2)
という関係があります。ωというのは角速度という量で、
1秒間に1回転するときの角速度が、2π (rad/s)
と定義されます。1回転分の2πという角度は単位がラジアン(rad)で、360度に相当します。回転中心からの距離Rのところにある物体を角速度ωでグルグル回すと、その物体の速度はRωということになります。
Rがタイヤ実効半径であれば、Rωというのはタイヤ実効半径の速度であり、これは当然、車速Vに等しくなります。それが式(2)の示すところです。
ところで、タイヤ＋ホイールの慣性モーメントをJ(kg*m^2)とすると、この回転体の回転運動エネルギーは、
・・・(3)
これに先ほどの式(2)
を代入すれば、
・・・(4)
一方、速度Vを持つ質量mの物体の並進運動エネルギーは、
・・・(5)
この式が、先ほどの回転運動エネルギーに等しいと置けば、
・・・(6)
これをmに関して解くと、
・・・(7)
これは、
慣性モーメントJの効果は、あたかも、非回転体部分の質量がJ/R^2だけ増大したのと同じように現れる
ということを言っています。例えば、ホイール＋タイヤの慣性モーメントが
の場合であれば、タイヤ実効半径を0.334mとして、
となります。 0.1(kg*m^2) の慣性モーメントは、あたかも加減速時に0.896kgだけ非回転部分の質量が増大したかのような効果を発揮する、というわけです。
ただし、以下に注意してください。非回転部分の質量が増大したかのような効果を発揮する、とはいっても、
- 加速や減速、すなわち速度変動する場合に限って表に現れる
- タイヤ路面抵抗の増大に寄与する質量の項、また、定速登坂時の仕事を増大させる質量の項としてはカウントされない
という性質があります。
カブラボ実験結果から慣性モーメントを推定する
鏑木氏の実験結果からホイール＋タイヤの慣性モーメントJを算出してみます。もう一度、式(1)を眺めてみます。
・・・(1)
ダンベルが持っていた位置エネルギーmghが、ダンベルの運動エネルギー
とホイールの慣性モーメントの運動エネルギー
に配賦された、という式です。この式(1)で、
- m：ダンベル質量3 kg
- g：重力加速度 9.806 m/s^2
- h：チェン長さ 0.9 メートル
- v：ダンベルの最終速度・・・ホイールの車速最終速度Vと11Tスプロケの半径とタイヤ実効半径Rから算出できる（11Tスプロケの半径は2.22 cmです）
- ω：ホイールの車速最終速度Vとタイヤ実効半径Rから算出できる
というわけで、式(1)で慣性モーメントJ以外はすべて、与えられていることになり、慣性モーメントJは式(1)を変形して次の式で算出可能ということになります。
・・・(1)’
その結果がコレ。中段の赤枠に各銘柄の慣性モーメントの計算結果を示します。また、下段には、加減速時に現れる慣性モーメント効果を、式(7)を使って非回転部分の質量増加に換算した場合の見かけの質量増分を示します。
カブラボ実験結果の数値を使って算出した慣性モーメントの値
慣性モーメントの数値。これはかなり尤もらしい値になっています。空力などのフリクション要素を無視した結果ですので、実際の値よりも大きく推定されていると思われますが、簡単な実験から得られる数値としては十分であると思われます。
それから非回転部の質量増加に換算した場合の増分⊿mですが、当然とはいえ、デュラR9100が小さいですねぇ。ホイール＋タイヤの重量でR9100はRS100の66%ですが、⊿mで見ると59%になり、R9100の軽さがさらに強調されます。つまり、
ホイール＋タイヤの軽量化で想像される以上に、加速時の軽さが際立つ傾向を持つ
ということになります。
これが体感として、また実測タイム差としてどの程度なのかは、また別問題ではありますが。
結局、加速でどの程度の差がつくのか
ホイールの慣性モーメントが変化すると、一体、どれだけの差が加速で発生するのか？
結局のところ、そこが知りたくなりますよねぇ。
回転体辺縁の重量物、つまりリムとかタイヤが重いと、慣性モーメントが大きくなるから、加速が不利になる。でも、ひとたび速度が乗ったら、今度は速度維持が楽になる。車重が同じでも慣性モーメントが小さくなっている方が登りも楽。これは常識。
なーんて、仮に、どなたかがおっしゃっていたとします。
そうですか？
どの程度、加速が不利なわけ？
どの程度、速度維持が楽なんですか？
慣性モーメント自体の大小が登坂に影響する理由は？
本当に常識？
常識の定義って、何？
・・・
こういう話は一度くらい、疑ってもよいと思いますよ。「車重が同じでも慣性モーメントが小さくなっている方が登りも楽」などという話は即、却下ではありますが。
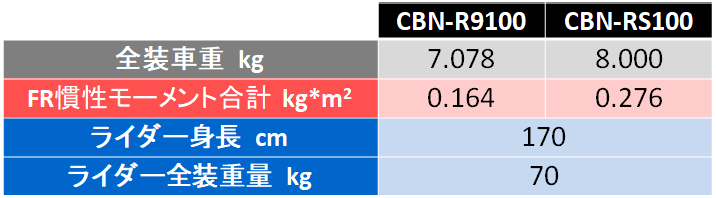
デュラR9100と、廉価ホイールRS100、これを机上対決させてみます。フロントホイールも考慮します。フロントの方が多少軽いので重量では差が出ますが、慣性モーメントは辺縁部のリムとタイヤが大勢を決めますので、次の表のように、前後を同じ値としておきます。前後ホイールの合計重量では0.922 kgの差があります。
前後（FR）ホイールの仕様設定
次に自転車を用意します。
廉価版RS100を履いたロードバイクCBN-RS100の全装車重を8 kgとします。これに対してデュラR9100を履いた軽量ロードCBN-R9100の全装車重は前後ホイールの重量分だけ軽くなって、7.078 kgです。なお、ホイールを替えただけで、それ以外は全く同じ仕様であると仮定します。
ライダーは身長170cm、ウエアも含めた全装体重を70 kgとします。自転車とライダーのスペックを次にまとめました。
自転車CBN号とライダーの仕様設定
というわけで1000mタイムトライアルで勝負！
先ほどの表の通りで、CBN-R9100はCBN-RS100よりも車重が0.922kgだけ少ないですね。そして慣性モーメントは0.122kg*m^2だけ少ない。これは非回転部質量に置き換えて表現すると1.012kgに相当しますので、加速仕事に効く質量増大は見かけ上、1.934kgの差となります。
さて、これを机上でどうやって評価するのか？
便利なツールがあります。次のリンク先に収納されている” RoadLoadSurveyor (ver.1.30) ”です。タイムトライアルや一定パワー巡航、一定速度巡航、ヒルクライム、惰性走行などのパワー収支計算が、標高や風力の影響も入れてEXCEL上で出来てしまうという、中学生の夏休みの自由研究にも好適な実にレトロフィットな代物。
cbn FILE REPOSITORY
完全にコンディションが保たれた同じライダーが乗車したとしても、違う自転車で走ったら出力の時間プロフィールだって微妙に違ってくるはず。1000mTTの計算なんて、一体どうやるんだ？？
こんな素朴な疑問が浮かびますが、このEXCELツール。ライダーの限界トルクを固定ギヤのケイデンスの関数で定義し、さらに、限界トルクと限界ケイデンスが時間とともに劣化することで刻々と変化するライダー特性をモデル化するという、実にうまいやり方で実装しています。
空力から、ギヤ比依存となる駆動系の効率の扱いにまで及ぶ、笑えるほどに詳細な取説も用意されていて助かります（笑）。このツールの作者自身が、こんな計算を普段EXCELでやっているとは到底、思えませんが。
これの赤タブのシート【1000mT.T.】を使います。なお、詳細は割愛しますが、限界トルクやケイデンス、それらの劣化に関するパラメータは、デフォルト値から適当に変更しています。
赤タブのシート【1000mT.T.】を使う
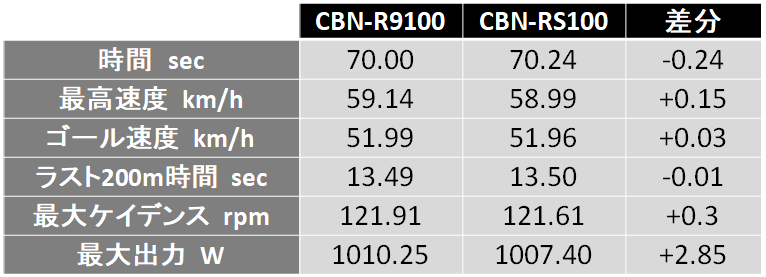
というわけで計算結果は次の通り。
【1000mT.T.】の結果一覧
軽量ロードCBN-R9100と廉価ホイール分だけ重いロードCBN-RS100のゴール時間の差は0.24秒。これはゴール時点で3.56 mの差に相当します。というわけで、
1000mタイムトライアルにおいて、ホイールの重量差と、慣性モーメントの差による効果は明らか
です。しかし、実際には、選手のコンディショニングのばらつきによる差の方が大きいのではないか？と思わせる程度の差です。
次に、時間による推移を見てみましょう。
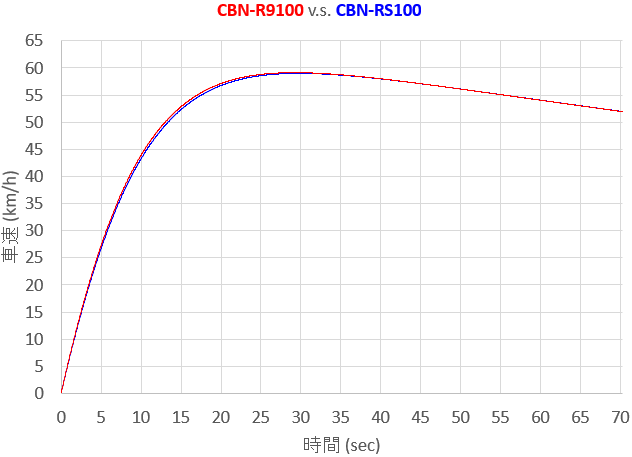
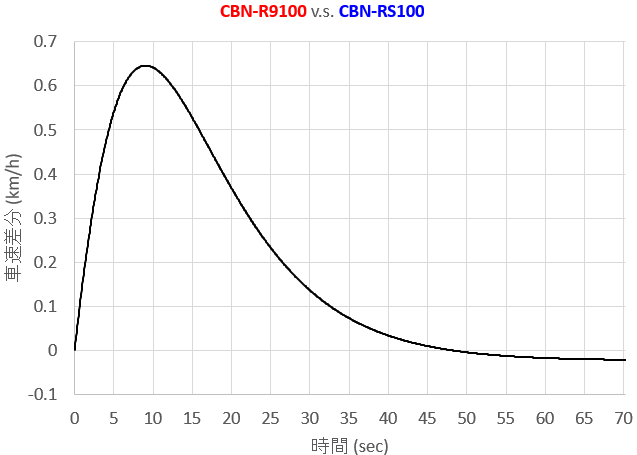
次のグラフは、スタートからゴールまでの車速の推移です。赤線がCBN-R9100、青線がCBN-RS100です。ちょっと差がわかりにくいですねぇ。
スタートからゴールまでの車速の推移
次のグラフは先ほどの車速の差分の推移です。
スタートからしばらくは加速走行の時間帯ですので、序盤で車速差が一気に大きくなっているのがわかります。しかしその後、車速の差は縮まり、47秒付近で何と、今度は重いCBN-RS100がわずかですが車速で逆転します。
これは、ライダーの限界トルクが劣化することで最高車速を示す30秒手前付近から加速走行ではなく、減速走行に移行することで、車両やライダーの質量と慣性モーメントがもつ運動エネルギーが逓減し、これが走行維持に配賦されるためで、「重いほうが速度維持が容易」、という現象につながります。
ただし、ライダーのモデリングとの兼ね合いもあり、計算結果の詳細な解釈には注意を要するところです。
走行距離の差分の推移
次のグラフは、走行距離の差分の時間推移です。CBN-R9100は序盤のアドバンテージを維持し、終盤にむかってわずかに差を詰められますが、最終的に3.56mの差をつけて1000mを走り切ります。
スタートからゴールまでの車速差分の推移
先ほど、1000mタイムトライアルにおいて、ホイールの重量差、慣性モーメントの差による効果は明らか、と述べましたが、これは1000mタイムトライアルという状況においてそうである、というだけの話です。
例えば平坦路中心のロードレースにおいては、様々な戦略や、位置取りによる路面の差、様々な状況変化の影響のほうが支配的で、さらには、車重や慣性モーメントよりもタイヤ選択のほうが重要で、この2台の、ホイールに起因する程度の重量や慣性モーメントの差は、空力も含めたそれ以外の車両条件が同じならば、ほとんど無意味になると思います。
つまり、どちらの自転車で走っても、そのこと自体が結果に影響を与えることは、まずない、と私は考えています。まあしかし、乗り手にしてみれば、軽い自転車に乗りたい、乗り心地の良い自転車に乗りたい、という気持ち的な面は無視できないし、そのおかげで余計に力を発揮することができる、という事もあるでしょう。（あれっ、こんなこと言っちゃいけなかったかな～？）
****
ところで、ライダーの体重も含めた質量やホイールの慣性モーメントの加速仕事と、空力抵抗に抗する仕事、転がり抵抗に対する仕事など、乗り手の出力が一体、どこにどれだけ配賦されているのか？
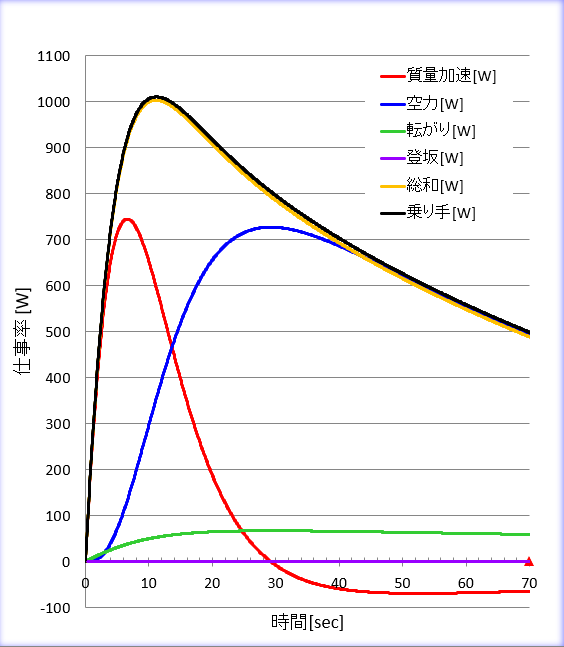
参考までにそのグラフを最後に載せておきます。これは軽いほうの自転車の結果です。じっくりご堪能下さい。なお、このグラフは、今回使ったRoadLoadSurveyor_ver.1.30のシートに掲載されています。
1000mT.T.において、乗り手の出力はどこにどれだけ配賦されるのか？
少し解説します。
- 赤線は、質量と慣性モーメントを加速するために使われる仕事(W)です。6秒付近で最大となりますが、加速度が最大となるのはスタート直後です。
30秒手前あたりから先で負値になりますが、これは減速していることを示します。減速時は、車両と乗り手の質量と慣性モーメントが持つ運動エネルギーが徐々に低下しますが、このエネルギーの行先は、乗り手の出力のアシスト、です。
極端な言い方をすると、体重ゼロ、車重ゼロ、慣性モーメントゼロの場合、運動エネルギーもゼロなので、ペダリングをやめたその瞬間に、空力抵抗と転がり抵抗に阻止され、惰性走行することなく、瞬間停止します。
自転車で惰性走行が可能なのは、体重や車重があるからです。
- 青線は空力抵抗です。自転車や乗り手に対する空気流れが乱流であると仮定すると、空力抵抗力は速度の二乗に比例しますが、クルマや自転車の空力抵抗も速度の二乗に比例すると考えるのが一般的です。
そうすると、パワーでは三乗に比例することになりますので、速度増大と共に急激に大きくなります。30秒手前で最大値となりますが、同時に速度も最大値となります。
- 緑線は転がり抵抗です。転がり抵抗力は定数であるとしていますので、パワーで見ると車速に比例します。
1000mタイムトライアルのような限界出力走行では転がり抵抗が相対的に小さく見えますが、これがサイクリング速度だとすると、相対的に占める割合が大きくなります。タイヤの選択は極めて重要です。（私は結構、無頓着ですが・・・）
- オレンジ線は、以上のパワーの総和で、後輪タイヤ接地部が地面を後方へ押しやる仕事を示しています。
- オレンジ線よりわずかに大きい黒線は、乗り手がクランク軸に投入するパワーを示します。黒線とオレンジ線のわずかな差は、トランスミッションによる損失を示しています。
“RoadLoadSurveyor (ver.1.30) “に実装されたトランスミッション損失の元ネタの論文によれば、高出力走行であるほど、トランスミッション効率が高い、という結果になっており、黒線とオレンジ線のわずかな差は、それを反映しています。
まとめ
1000mタイムトライアルにおいて、WH-R9100-C40-TUとWH-RS100のホイールの重量差、慣性モーメントの差による効果は明らかである
謝意
実に面白い数値ネタを提供してくださるカブラボ主宰、鏑木裕氏に深謝します。
参考
CBN本館には、ホイールの慣性モーメントを実測するレビューが何と、3件も投稿されています。う～む恐るべし、CBN！
▼ GlennGouldさんのその他の自転車考察系記事はこちらから読めます
