体重の神秘（笑）

今年の赤城山ヒルクライムには、9キロの減量を成功させて臨むつもりだ。というわけで、今週月曜日から社食の昼食では、

ごはん、超小盛でお願いします

これで毎日100グラムの減量になり、3か月後には9kgの減量に成功するはずだ。「継続は力」ってわけさ。フフフフ・・・

ところが一体、どういうことなんだっ！

月曜日朝の体重は78.4kgだった。木曜日の今朝、さっそく成果を確認しようと3日ぶりに体重を計ったのだが、な、何と、体重は78.55kgだ。減るどころか150グラムも増えてるじゃないか。なっ、何故だ。なぜ、昼のご飯の量を超小盛りにしているのに増えちゃうんだ！？

この現実をどうしても受け入れることができない。お、おれは、何かに憑りつかれているのだろうか。

厳しい競技の世界に身を置く方は特に、日々の体重管理に気を使っているのではないかと思います。

シーズン前に一気に減量する

とか、

運動量を少し増やして、摂取カロリーを少し落として一日100グラムのペースでゆっくり減量する

とかとか。。。

自分の走りの特徴が際立つ体重と筋力のバランスとか、ヒルクライムで自己記録を縮めて上位に食い込むためのベスト体重の設定といった難しい課題に、色々な情報や独自の哲学を織り交ぜて取り組んでいるのが「アスリートな方々」なのかなぁ、と勝手に想像してしまいます。

ただ単純に自転車通勤とかサイクリングするだけの私など、体重を計って、「増えてるなー」とか「あれれ、最近減り気味だぞ？」みたいに思うことはあっても、マジメに体重管理するなんてことは、まずありません。

そんな私ですが、じつはかれこれ24年ほど毎朝、起床時に体重を計測しています。体重というのは水分摂取量や発汗量、食べる量に応じて日々、数100グラム程度は簡単に上下してしまうもので、計りはじめた当初は、

ええーっ？ずいぶん変動するもんだなぁ

と思ったものですが、何年もやっているうちに、おなかの微妙な起伏を見ただけで、結構な精度でその時の体重を言い当てるなどという、ある種の特技を習得するに至ります。（←ｱﾎ）

そんなこんなで溜め込んだデータですので、どうせなら・・・というわけで、このなかから、1997年1月1日から2020年1月1日までの23年間、8401日のデータをじっくりと眺めてみました。自転車競技者にとって必要不可欠な体重管理につながる何かが、もしかしたら見えてくるかも知れません。

（←実は何も見えてきません。悪しからず！！）

体重は日々、激しく変動する
体重変化のトレンドを的確に捉えるには
周波数解析から見えてくるもの
パワースペクトル密度(PSD)の右下がり特性の意味
生きている証
まとめ

体重は日々、激しく変動する

まずは、23年間の計測結果を俯瞰します。

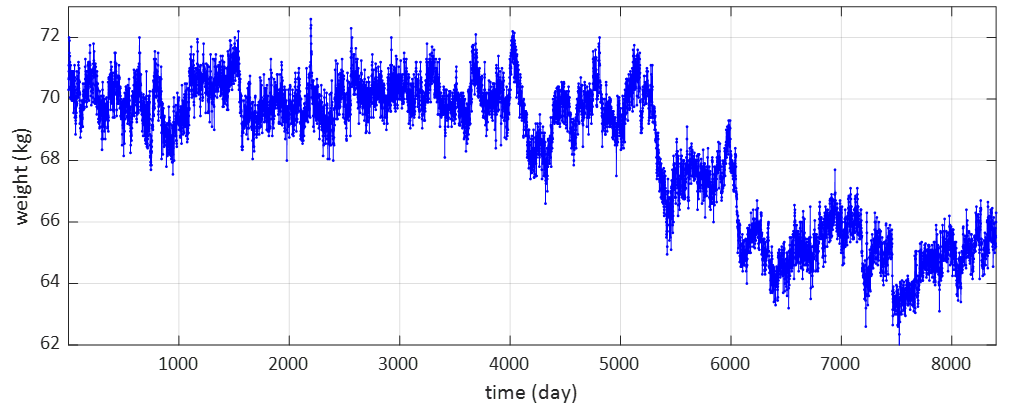
図1 日々の体重変化

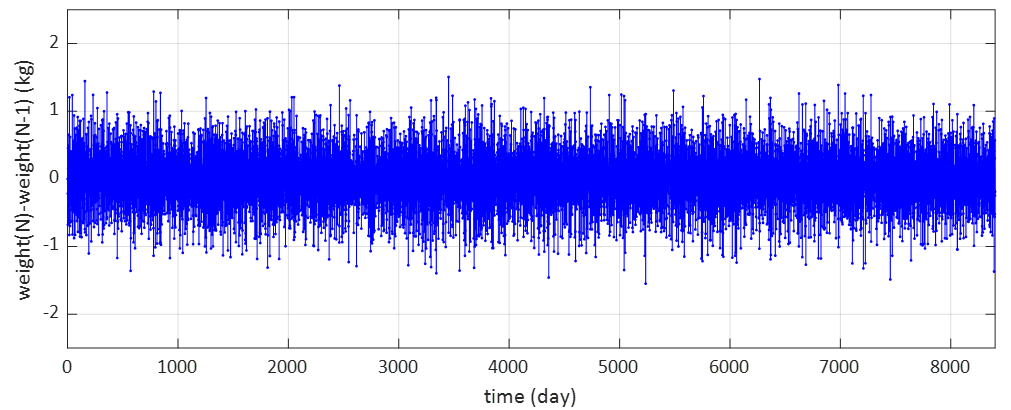
図1は日々の体重を表しています。横軸は23年間、8401日の幅になっています。全体の平均値は68.334kgです。体重計は当初、TANITAの100グラム計を使っており、例えば68.1kgと68.2kgを行き来するような表示になる場合には68.15kgを採用し、見かけ上、50グラム刻みの計測としています。その後、途中からOMRONの50グラム計を使っていますが、50グラム刻みでのデータ記録はそのままです。

なお、年間のうち数日は計測しない日がありますが、その日の体重は、「多分こんなもんだろう！」と、結構な精度を誇る(笑)脳内体重計の推定値を用いています。大勢に影響はないでしょう。

上のグラフではずいぶんと体重が細かく変動しているように見えます。これをはっきりさせるために、当日と前日の体重の差分をグラフにしてみます。つまり、前日の体重から1kgだけ増えたらプラス1、1kgだけ減ったらマイナス1、などとしている、という意味です。

図2 当日と前日の体重の差分

実に、最大でプラスマイナス2kg近い振れ幅があります。どういうことかというと、たった1日で朝の体重が1kg以上増えたり減ったりすることがザラにある、ということです。

しかし、1日単位で腹に1kgも肉がついたり落ちたりするはずもなく、この変動の大半は、水分摂取量や食事量、発汗量、大腸に滞留するうんち君の量などの、日々のばらつきによるものです。

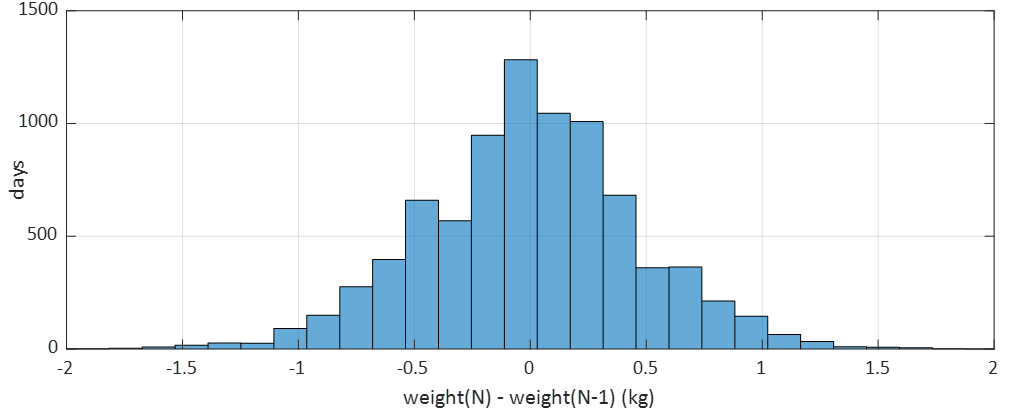
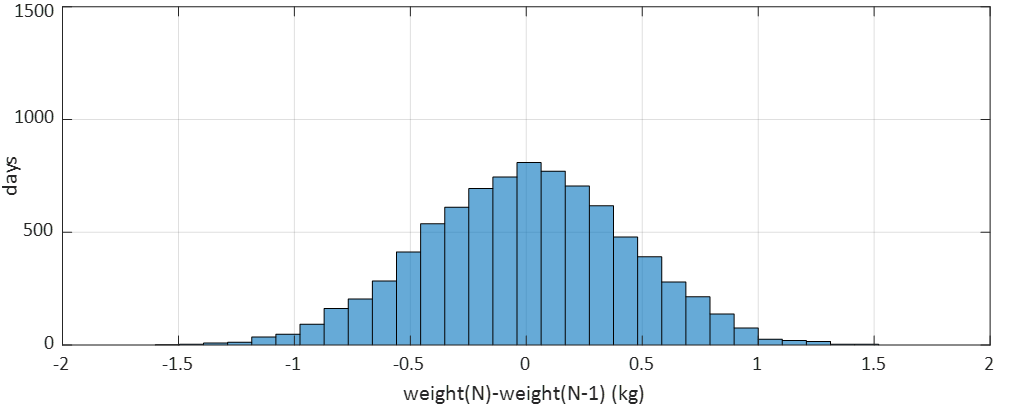
図2をヒストグラム（体重の頻度分布）にするともう少し分かりやすくなります。

図3　当日と前日の体重の差分のヒストグラム

当日と前日の体重差は、ゼロ近辺の頻度がほぼ最大です。そりゃまあ、そうですよね。そしてプラスマイナス0.5kgの体重差の範囲内の面積が、全体の面積の70%程度、すなわち、プラスマイナス0.5kgの体重差の範囲に70%程度の確率で入ってくることがわかります。結局、

あれっ、たった1日で1キロも増えちゃった！

などということも時にはありますが、驚くことはない、ということです。ダイエットなどされている方は、日々の体重増減に一喜一憂する必要などなく、1週間単位といった期間の変動に注目するべきでしょう。

体重変化のトレンドを的確に捉えるには

体重というのは日々結構な勢いで変動することがわかりました（いやまあ、自分のデータなので、そんなに変動するのは自分だけかも知れませんが）。というわけで、ダイエットに挑戦されている方は、そんな日々の増減に一喜一憂しないためにも、体重変化の大きな傾向を把握する必要があります。

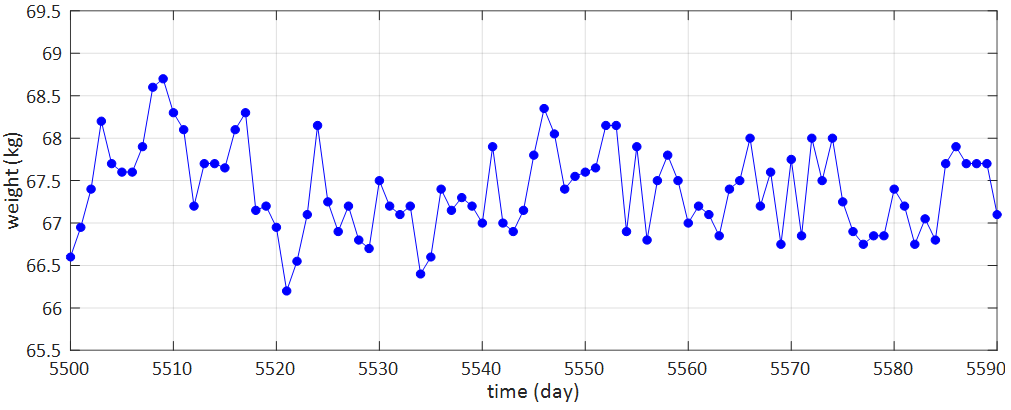
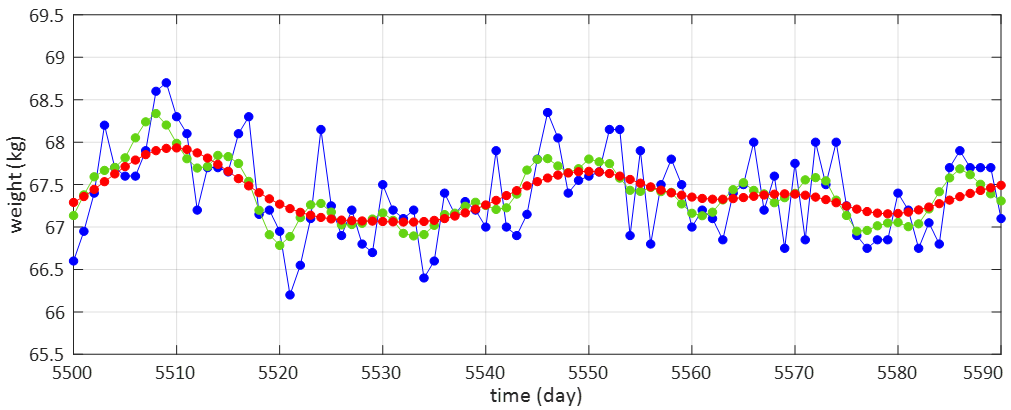
最初のグラフはデータが多すぎてよくわからないので、今度は3か月分のデータで日々の変動を眺めてみます。次のグラフは5500日目から91日間の体重を抜き出したものです。

図4　91日間の体重変動の事例

毎日飽きもせず体重が変化しているのがわかると思います。こんな日々の増減に一喜一憂しないためには、どうすればよいか？

こうすれば、いいんです！（川平慈英風）

図5　オリジナルデータと平均データの比較

青●：オリジナルデータ
緑●：1週間平均
赤●：3週間平均

図の青がオリジナル、緑が、1週間のデータを平均して日々の激しい増減の影響を緩和させたもの、赤は3週間のデータを平均してさらに滑らかにしたものです。

3週間分のデータを使って平均化した赤線は、体重変動の真ん中を滑らかに捉えて推移していることがわかります。日々変動する青線ではなく、真ん中を滑らかに貫く赤線で体重管理するのが適当でしょう。

じゃ、このグラフをどうやって得るのか?

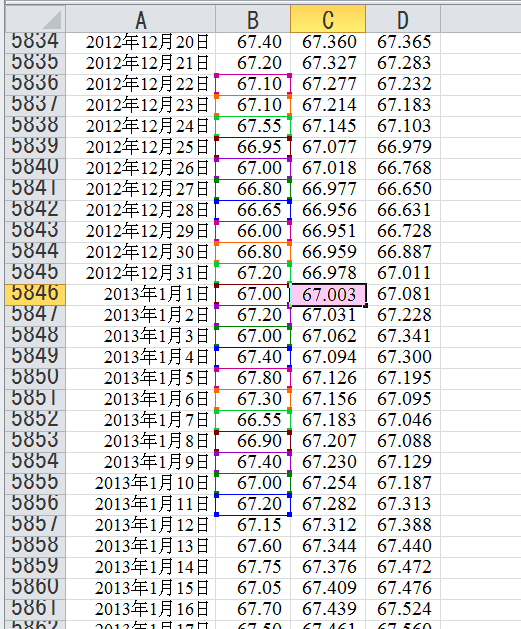
ご多分に漏れずこういう数字の管理はエクセルみたいな表計算ソフトが便利です。次の図。

図6 重みづけを実施してデータを作成する

この図で、

A列→日付
B列→体重計の値
C列→21日分のデータを使って得た体重
D列→7日分のデータを使って得た体重

です。2013年1月1日に着目して21日平均を説明します。1月1日の≪21日平均≫は、

B列の21個のデータを使ってC列の体重≪67.003kg≫を導く

ということをやって得ています。2013年1月1日と、その前後10日ずつ、図のB列セルで四角い色枠で囲まれた合計21個のデータを使うところがちょっとした特徴ですが、したがって、2013年1月1日のC列での値というのが判明するのは10日後の2013年1月11日ということになります。

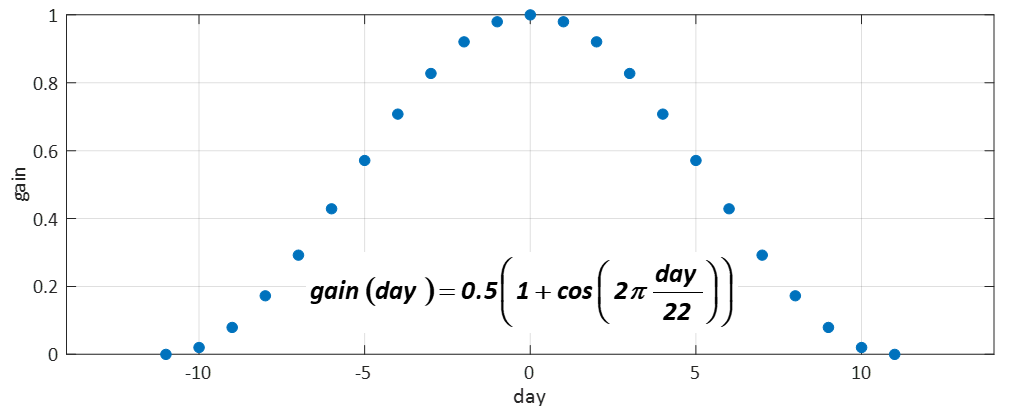
実はこの21個のデータ、単に足し合わせて21で割っているというわけでもありません。まあ、それでも全然よいのですが、私は次のような関数で重みづけを行っています。

図7 重みづけ関数

つまり、2013年1月1日の体重の重みづけを最大として、離れるほど重みづけを小さくしています。

これはよく知られた重みづけの方法で、こうすることでちょっとだけいいことがあるのですが、この関数が何者なのか、何がいいのか、といった説明は省略します。重みづけの具体的数値を次に示しておきますので、実際にやってみようという方は、参考にしてみてください。下図で、左側が21日平均で使う重みづけ、右側は7日平均で使う重みづけです。

	21日平均の重みづけ	7日平均の重みづけ
-11	0
-10	0.02025351319
-9	0.07937323358
-8	0.172569633
-7	0.2922924935
-6	0.4288425809
-5	0.5711574191
-4	0.7077075065	0
-3	0.827430367	0.1464466094
-2	0.9206267664	0.5
-1	0.9797464868	0.8535533906
0	1	1
1	0.9797464868	0.8535533906
2	0.9206267664	0.5
3	0.827430367	0.1464466094
4	0.7077075065	0
5	0.5711574191
6	0.4288425809
7	0.2922924935
8	0.172569633
9	0.07937323358
10	0.02025351319
11	0

↑ 図表8 重みづけ関数の数値

21日平均用の重みづけ係数は、全部足し合わせると11になるので、これらの係数を掛けた体重を全部足して、それを11で割れば、21日平均の体重が得られる、というわけです。同様に7日平均は係数和が4なので、これらの係数を掛けた体重を全部足して4で割れば、7日平均の体重が得られることになります。

あれぇ？数えたら21日じゃなくて23日のデータ数じゃないか？

そうなんです。でも一番端っこの重みはゼロなので、これは事実上、扱いません。したがって21日という風に表現しています。7日平均も実は9日のデータですが、同じく両端がゼロなので7日。あしからず！

周波数解析から見えてくるもの

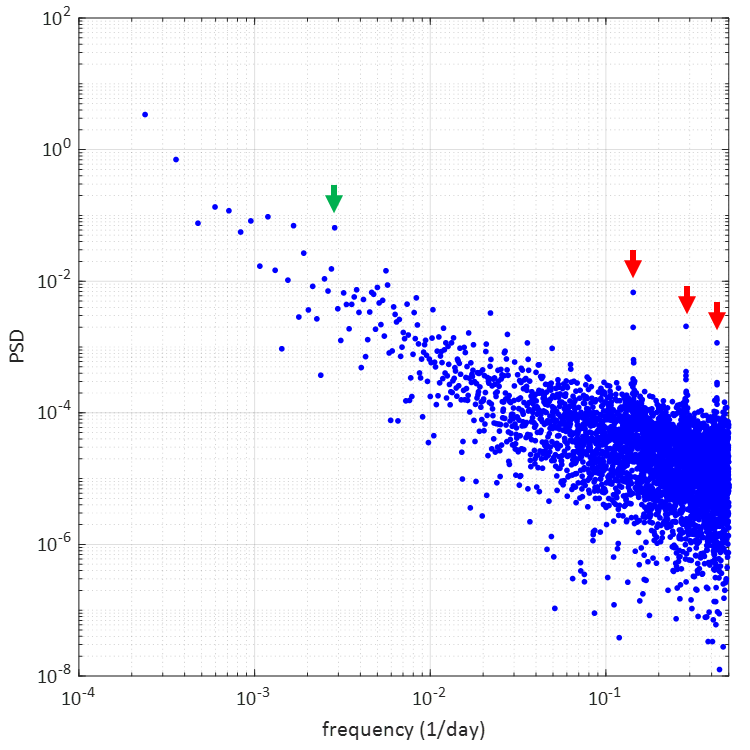
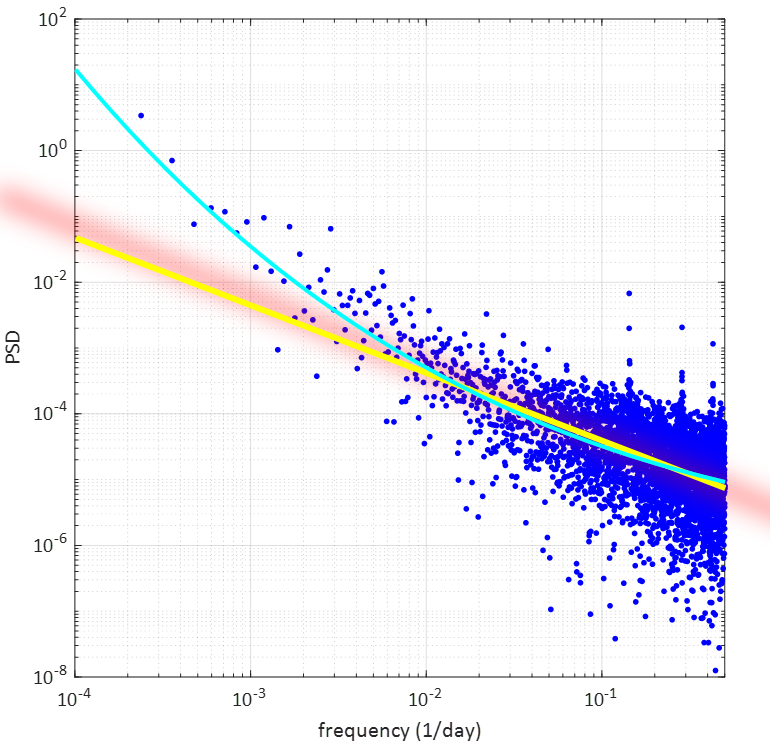
いままでは時間軸上で体重変動を眺めてきましたが、周波数軸上で眺めてみます。時間軸上のデータが持つ情報量を1つの欠損もなく周波数軸上に移行させる方法として、フーリェ変換という数学の道具があります。面倒な説明は省略して、フーリェ変換を行った結果を以下に示します。この表示形式はパワースペクトル密度(PSD)と呼ばれるものですが、理論的背景は割愛！

図9 体重データのパワースペクトル密度(PSD)

横軸は時間の逆数で1/dayすなわち周波数(frequency)となっています。オーケストラのピッチ合わせの音が、通常の室温では概ね440Hz（真ん中のラ音）あたりになったりするのですが、このHz (ヘルツ)が周波数の単位です。普通、周波数といえばコレです。1秒間に440回だけ振動するのが440Hzというわけ。

では、この図の横軸1/dayで、例えば一番右端に相当する0.5のところは何かというと、2日分の1 = 0.5、すなわち2日、つまり172800秒で1回だけ振動（変動）する成分の大きさを示しています。参考までにHzで表示すると0.0000058Hzです。(低っ)

ここで注目したいのが、上のグラフの右側に位置する10のマイナス1乗つまり0.1、すなわち10日分の1よりも高い周波数の領域です。赤矢印で示したように3つの極めて明確なピークが見られます。1番左側矢印のピークの周波数は7日分の1、すなわち周期でいうと、1週間。その右のピークが7日分の2、その次が7日分の3です。

特に7日分の1すなわち1週間周期のピークがはっきりしているのですが、これは1週間単位の生活リズムを反映しているものでしょう。つまり、毎週5日間は働き、土日は休日で食生活も多少変化する、という1週間をひと区切りとする日々の営みが図らずも体重変化の中にはっきりとあらわれている、ということです。

この変化は1週間で1周期ですが、正弦波的ではないため、1週間の整数倍の高調波成分が発生します。これが7分の2と7分の3という周期が同時に現れる理由です。

1日1回しか計測していないので、横軸は周期が7分の3.5までしか計算されません(その理由は省略します)が、もし、12時間ごとに計測して1日2の回計測を行えば、このグラフの中に7分の7、すなわち1日周期の変動も見えてくるはずです。

やはり、1週間という変動周期は生活リズムの面からも、とても基本的な周期なんですねぇ。

一方で1週間周期よりも長い周期の変動では明確なピークは見当たりません。強いて言えば0.00274つまり365日分の1のところにピークがあります。図中の緑色の矢印のところのピークがそれです。1年を周期とする季節変動成分です。

このピークは、ボケーと眺めると、偶然のピークのように見えますが、365分の1のところにわざわざ位置していますから、間違いなく、1年周期のピークでしょう。こういうピークは、4、5年程度の長さのデータではデータ長さが足りず、現れなかったかもしれません。

パワースペクトル密度(PSD)の右下がり特性の意味

もう30数年ほど前の話ですが、半導体の雑音の周波数特性などで現れる1/f(エフぶんのいち)揺らぎ、というものが一般に知られるようになりました。半導体や電子回路などの雑音や、時計の中に入っている水晶振動子やGPS衛星などに搭載される原子発振器の安定度評価などの世界では、1/f揺らぎも含めてさまざまな計測や研究がなされています。

さらには、せせらぎの音や心拍の揺らぎは1/fの揺らぎ特性を持っているとか、J.S.バッハの音楽は1/f成分が強いとか、聖飢魔IIのあの曲も・・・とか、1/f揺らぎ扇風機とかとか。様々な誤解も含めて1/f揺らぎという言葉が独り歩きをした物件もありそうですが。

ところで体重のPSDに目をやれば

「おﾞおﾞーーっっ！」
「これってほとんど1/fの傾きじゃないか！？」

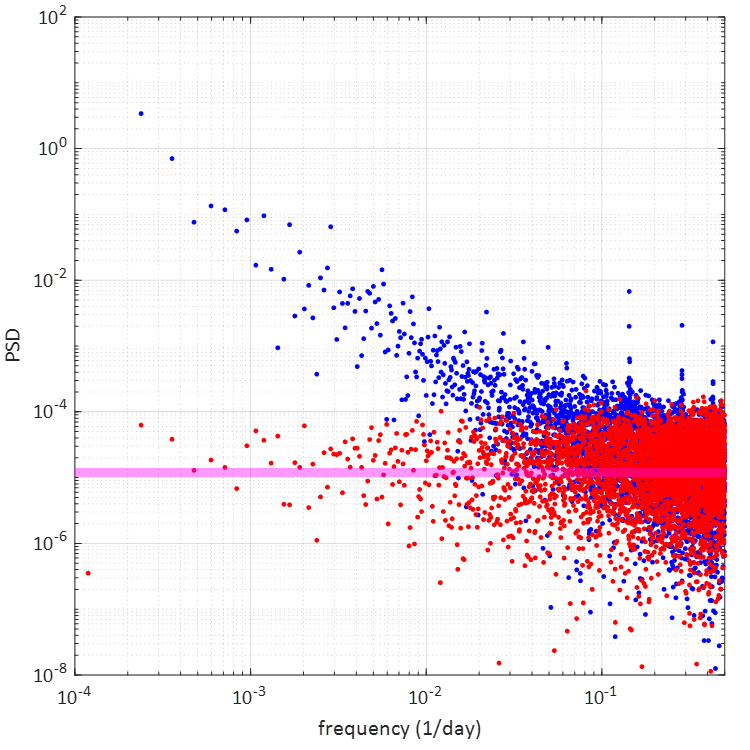
次のグラフで黄色い直線は、青い測定値を1次関数（すなわち直線）で近似したものです。赤い直線の帯は1/fの直線を示します。何ということでしょう。

黄色い近似直線はほとんど1/fの線そのもの

ではありませんか。もう少し詳しく見るために、青い測定値を3次関数で近似してみたのが水色の線。なるほど、10のマイナス2乗つまり0.01、すなわち100日周期よりも短い周期の範囲（グラフの右側）で1/f特性が際立っているようです。

図10 体重変動の1/f特性

これはもう、

えーっ、ま、マジですか？

と言いたくなる事態。

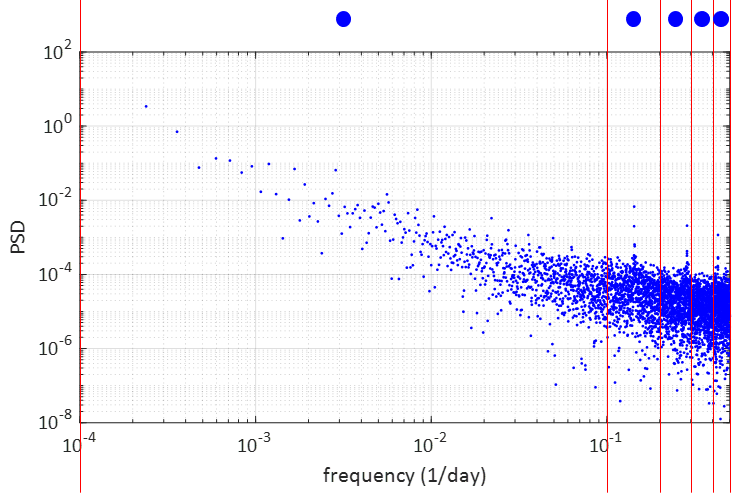
【注：グラフの左側で近似の黄色線が青データから大きく離れていますが、実は青データが周波数軸上では右側に極度に偏在して存在しているため、これに引っ張られて上図のような近似直線になります。青点の偏在度を示したのが次のグラフで、赤線で区分した各範囲に同じ個数のデータが入っています。つまり左半分はスカスカ】