その昔、伝説のシクロクロスタイヤ、コンチネンタルのTプロフィールを履いたロードで林道を飛ぶように駆け抜けていたという荒法師Bさん曰く、
師B 「最近、タイヤが太いよねぇ?」
宅浪 「はぁ」
師B 「何でだろうな?」
宅浪 「さあ」
師B 「いつの間にか21Cが23Cになり25、26、27と、あたしの人生、暗かった・・・」
宅浪 「それわかる人、Bさん世代が限界ですよ」
師B 「ヘッ、どうかな・・・フフフ」
相変わらずなに言ってんだ?
巻き込まれないように用心しつつ、宅浪は太くなる一方のタイヤに思いをはせた。
本稿では、超簡易なタイヤ変形モデルを作成し、これを使って、タイヤの転がり抵抗についてアレコレと考えてみます。例によって暴走気味ではありますが、どうぞお付き合いください!
タイヤの転がり抵抗って何だっけ?
走行することでタイヤが転がり、たったそれだけのことでタイヤの接地面からタイヤに向かって進行方向と逆向きの力が与えられて、走行の邪魔をする
これがタイヤの転がり抵抗です。
転がり抵抗係数”RRC”って何だ?
タイヤの垂直荷重に対する転がり抵抗荷重の大きさの比率を、「転がり抵抗係数」といいます。転がり抵抗係数つまり ”Rolling Resistance Coefficient” を略してRRCと、タイヤの世界では呼ばれています。
標準的な自動車用タイヤのRRCは0.01(すなわち1%)程度らしいのですが、RRCはいくつ?という場合、クルマの世界では何故か10000倍してわかりやすくするお約束があるようで、0.01×10000で、RRC=100と表記します。ダンロップの低燃費タイヤ 「エナセーブPREMIUM」 のRRCは61(すなわち10000で割って0.0061、つまり0.61%)らしいですよ。
というわけで、RRCと言った場合には、0.01と1%と100は、みな同じRRC値ということになります。自転車の世界ではどちらかというと0.01と表記する場合が多いような気がします。
となると、エナセーブ。RRCが0.0061でしたよねぇ。2トンのクルマであれば、4つのタイヤ接地面で、
2000 kgf×0.0061 = 12.2 kgf
この力でクルマを水平方向に押せば、ゆっくり前進させ続けられる、ということになります。もちろん、車軸の軸受けフリクションとか、前輪のトーイン影響とか諸々を無視して真っ直ぐ前を向いているタイヤだけを考えた場合ですので、実際にはこれだけでは動かないでしょうが。
真っ平らな良路の場合、クルマは意外と小さな力で押すことができますが、何となく理由がわかりますねぇ。
転がり抵抗はどこからやってくるのか?
転がり抵抗の主な発生原因は、タイヤ変形の非対称性です。つまり、凹(へこ)ませるときのへこみ量に対する力と、凹みから戻るときの凹み量に対する力の関係が異なることが主な原因となります。
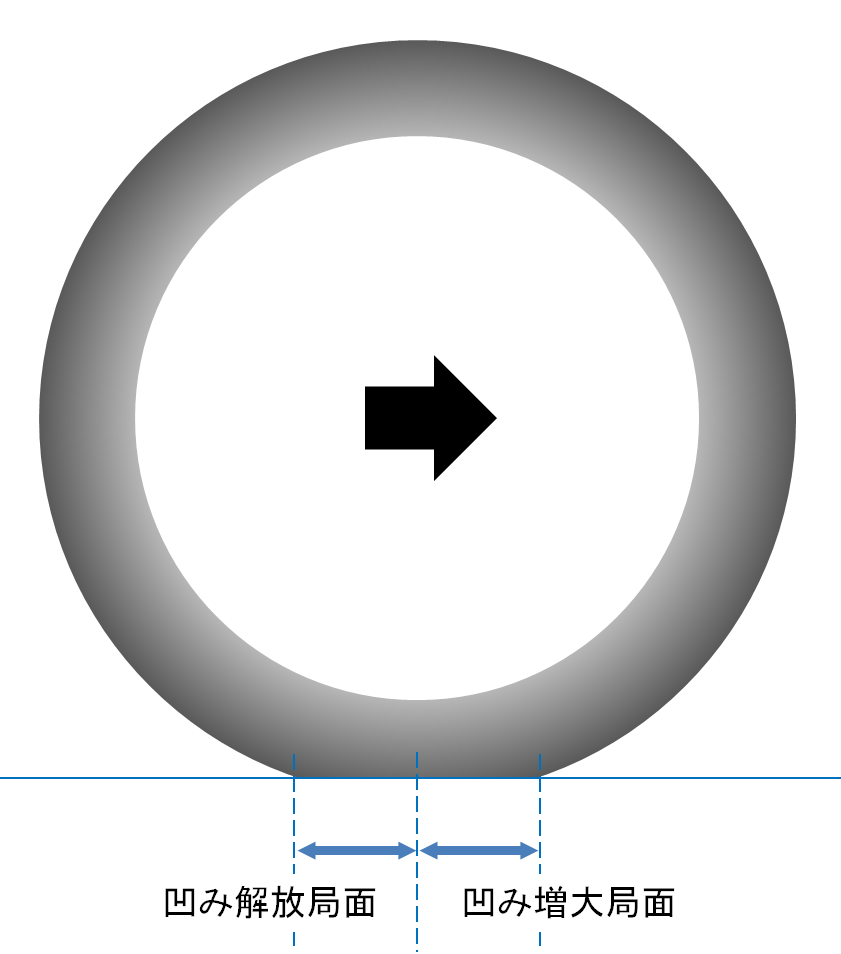
次の図をご覧ください。タイヤは右向きに転がり続けますが、この際、地面に接地を開始する側は凹み増大局面、接地から解放される側は凹み解放局面となっています。
上の図では、凹み増大局面と解放局面での凹み方を、左右対称として描いています。この際、変形に伴って地面がタイヤを押し返して凹ませる力が実は、左右対称にはなりません。
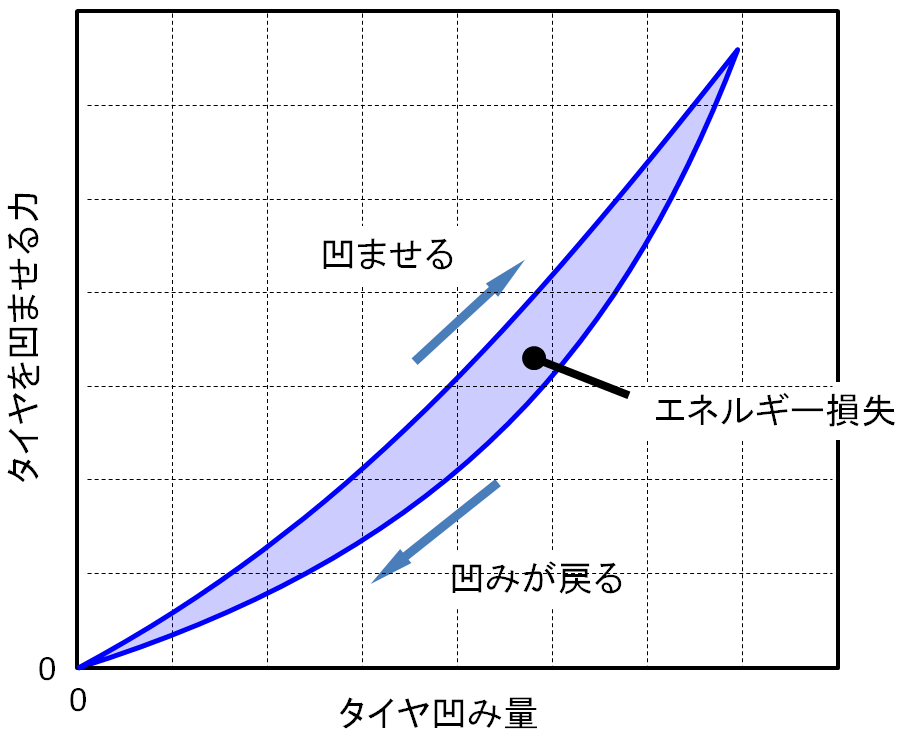
下図はかなり適当な模式図ですが、このように、凹み増大局面での力が、凹み解放局面の力を上回ります。タイヤのゴムというのは、まったく損失を生じない理想的なバネのような動作はできず、一度凹んでしまったタイヤは、ある意味、凹み癖がついてしまい、戻るときに地面を押し返す力が小さくなります。下の図ではタイヤ凹みの往路と復路で挟まれたところを薄い青で塗りつぶしていますが、この面積はエネルギー損失に相当します。また、こういうループを「ヒステリシス・ループ」と言います。
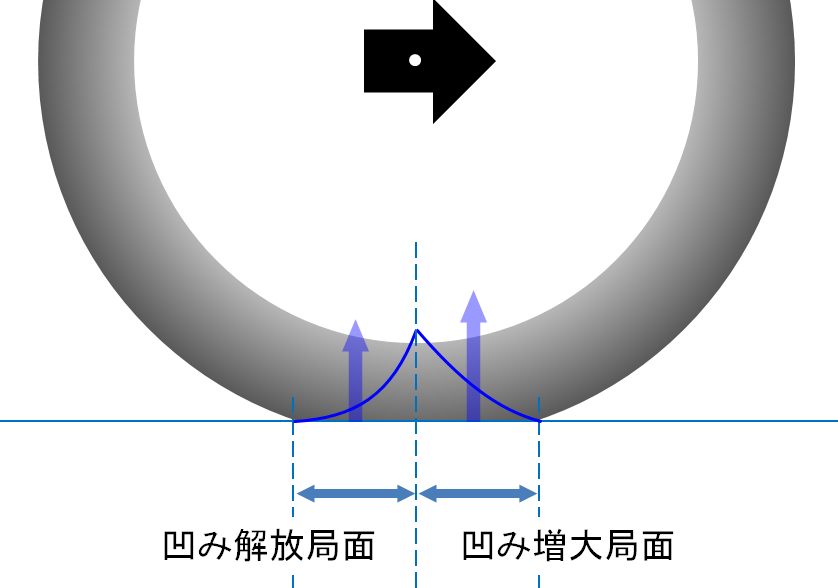
凹み増大局面よりも凹み解放局面で、タイヤを凹ませる力、つまり地面がタイヤを押し返す力が小さいという上の図。これをタイヤの接地面に模式的に書き写すと、次の図のようになります。左右対称にはならず、凹み増大局面の方が少し大きい、この力を、下図の薄青色の上向き矢印で代表させると、右側の矢印の方が大きくなります。この2つの力の差分が、自転車が進む向きと逆向きの推進力をホイールに与えます。これが転がり抵抗の主犯、です。
タイヤ転がり抵抗係数”RRC”数値の信頼筋情報
さて、自転車タイヤのRRCに関して、目の覚めるようなWEBサイトがあります。” BICYCLE ROLLING RESISTANCE” というサイトです。数年ぶりに覗いてみたらますます充実していました。
各種タイヤの転がり抵抗を、空気圧を変えて計測し、その結果を網羅するという、唸るしかない素晴らしいサイトです。使い勝手よくプログラミングされた制御計測機器と、この計測試験のために製作したシャシ・ダイナモ装置を駆使して、周到な手順を経て計測しており、信頼性が極めて高い、非常にしっかりしたデータが網羅されているように感じられます。こんなサイトがあるとメーカー側も意識してしまうでしょうね。
空気圧とRRCの関係 (信頼筋による実測結果)
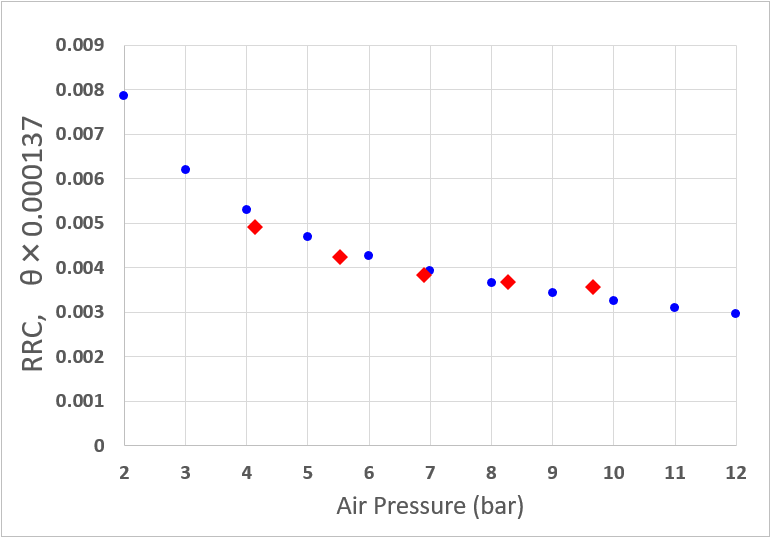
というわけで、超強力な上記サイトからデータを一組だけ引用します。タイヤ空気圧と転がり抵抗係数RRCの関係をグラフにしたのが次の図。
これはチューブラータイヤVittoria Corsa G+(幅25mm) の場合です。ハブシャフトにかかる負荷を42.5kgfに設定して転がり抵抗のパワー計測を行って得た数値です。御覧のとおり空気圧を大きくすると、転がり抵抗係数RRCが小さくなります。
転がりに伴う抵抗(Watt)もRRCに比例して小さくなりますので、こういうグラフを見てしまうと、「ちょっと空気圧を上げて転がりをよくしようかな?」なんて思ったりしますよねぇ。他の銘柄も同様の傾向です。まあそれにしてもRRCが0.004以下だなんて、ずいぶん小さいような気がしますが、ダイナモで回しているドラム路面が滑らかすぎるのかも知れません。
というわけで超簡易タイヤ計算モデルをつくってみた
こういう素晴らしいサイトを覗いてしまうと、
空気圧に対する転がり抵抗係数RRCと相関の高いタイヤの数値は一体、何なのか?
ということが、気になってしまうわけです。
というわけで 最も簡易なタイヤ計算モデルを作ってみます。何が見えてくるのだろうか!?
(やっとその話かよ)
モデルの作成は、タイヤの接地面がどういう形状になるのか?というところからスタートします。なお、ここで作るタイヤモデルは恐らく、最も簡易、笑っちゃうほどにイージーなモデルですので、数多くの制約があります。まあそこは、精度を上げる余地を存分に残してある、ということにしておきましょう!
接地面の考え方
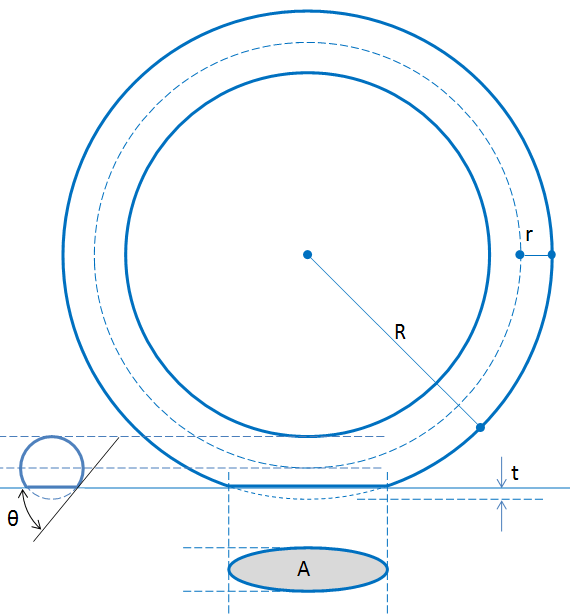
丸断面のタイヤの形状は、細長いドーナツのようなものです。このドーナツを下図のようにスパッと切り落とすと、楕円形風の面が出てきます。これをタイヤの接地面形状と見做します。もちろん、タイヤは厚さがあるゴムでできていて、しかもそれ自体が剛性を持ち、結構しぶといヤツ(!)ですから、ドーナツがスパッと切り落とされたような接地面を与える変形など、絶対にしません。しかしそこは、ナンチャッテだから、ということでやり過ごします。
図を説明します。
- 丸断面のタイヤが接地して現れたのが楕円風味の接地面積A
- 接地凹み量がt
- タイヤトレッド折れ曲がり角度がθ
これらは、タイヤ幅、タイヤ周長、空気圧で変化するはずです。また、ハブ軸荷重が零ならば、全く凹まないので、凹み量tが零になり、面積Aも零になり、タイヤトレッド折れ角度θも零となります。
タイヤトレッドが図のようにキレイに折れ曲るなどということは絶対にない!のですが、そこはお笑い簡易モデルに免じて。イメージとしては、ケーシングとかトレッドとかチューブの厚さがゼロで、限りなくフニャフニャな膜でできたタイヤ、です。このうす~い膜は、外力に素直に応じて変形して凹む一方で、空気圧だけはカンペキに受け止めてタイヤの形状を立派に維持する、というご都合主義的モデルです。(これが究極のチューブラータイヤという説も?)
また、真下に向かって力を加えているハブ軸から見込んだタイヤのばね定数、つまり
- 垂直方向のタイヤ剛性
も、タイヤ幅、タイヤ周長、空気圧で変化するはずです。
というわけで、最簡易モデルを採用した場合について、上記1,2,3,4の変化を網羅し、最初に引用した、「空気圧とRRC」の関係と相関の高い数値群を見つけてみることにします。
なお、ドーナツ、というかタイヤの形状を与える方程式、接地面積Aを与える楕円形っぽい図形の方程式、面積Aの計算方法、タイヤトレッド折れ曲り角度θを与える式、タイヤの垂直剛性の式などは、自分で導出する必要がありますが、その過程は省略します。(ご質問は大歓迎ですヨ)
計算条件
ハブ軸荷重は BICYCLE ROLLING RESISTANCE に準拠し、42.5kgfとしています。
計算結果 ~25Cタイヤで空気圧を変えてみる~
計算結果を示します。
接地面形状の変化
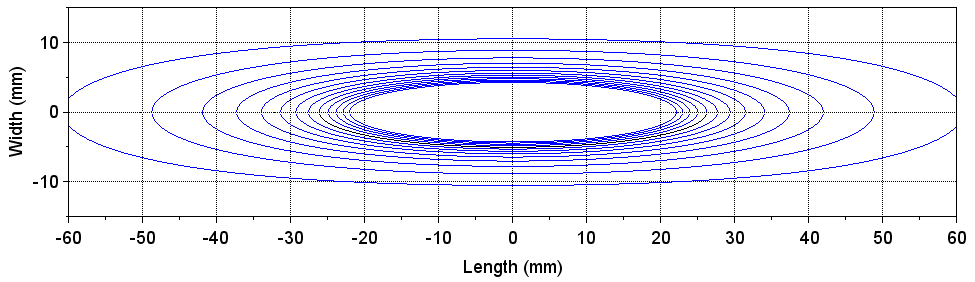
ハブ軸荷重が42.5kgfの時の、丸断面700×25Cの接地面形状を次に示します。なお、空気圧は2~14 barの1bar刻み、空気圧が小さいほどタイヤが深く変形して接地面積が大きくなります。そりゃそうだろう、という感じですね。図で目盛りの正方形が1平方cmですが、25Cで2barという空気圧はさすがにヤバそうです。
次の図が700×25Cと比べてタイヤ周長が33%ほど小さい20インチタイヤ、ETRTO406×25Cの結果です。
700×25Cの結果と同じように見えますが、僅かに短径が広く、長径が短くなっています。また、同じ空気圧で比較すると、形状は僅かに異なりますが、面積は同じです。これは、荷重Lと圧力Pと面積Aの関係が
L = P×A
となっていて、接地面のいたるところで接圧がPで一定であることに由来します。つまり、タイヤケーシングやトレッドゴムやチューブ自体の厚さは零でそれ自身は荷重を一切、支えず、あくまでも荷重を支えるのは空気圧と接地面積の積だけである、というモデルを採用していることを示しています。 ”ナンチャッテ簡易モデル” の所以です。
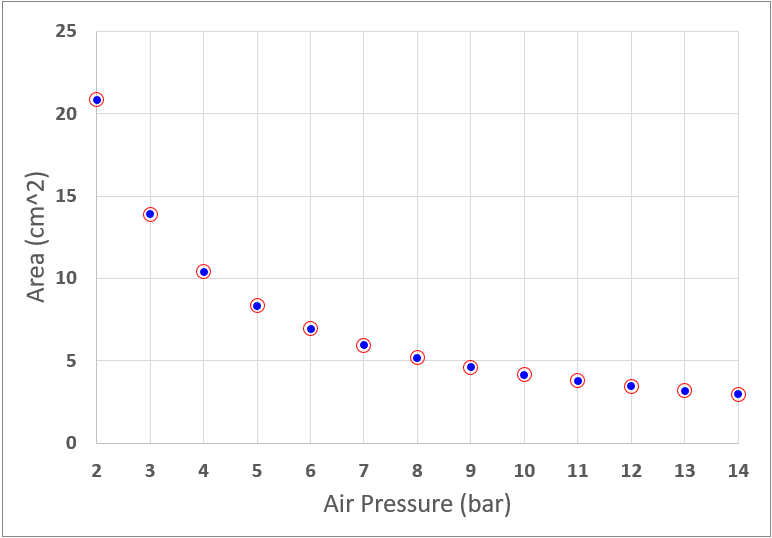
というわけで次に示すように、接地面積Aと空気圧の関係はタイヤサイズにかかわらず同じになります。青いドットが700×25C、赤丸がETRTO406×25Cの場合です。空気圧は2~14barです。
空気圧を低くすると接地面積が急激に大きくなります。さっそく、RRCの変化によく似たグラフが得られました。
凹み量tの変化
荷重を与えて接地することでタイヤが凹みますが、この凹み量t(mm)と空気圧P (bar)の関係を示します。青い点が700×25C、赤丸がETRTO406×25Cの場合です。小径タイヤの方が深く凹みます。つまり、車高がその分、低くなる。空気圧は3 barもあれば、どうにか走ることが出来ますが、2barだとフワフワでしょう。
タイヤトレッド折れ曲がり角度θの変化
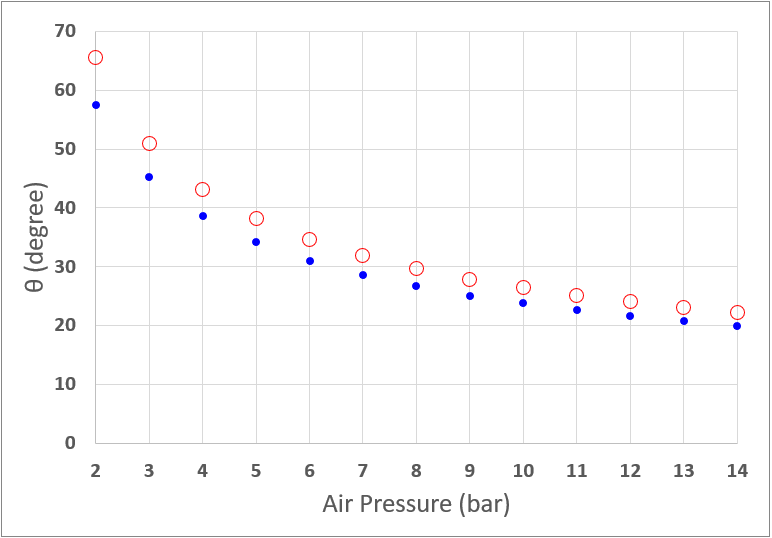
”タイヤトレッド折れ曲がり角度θ” の変化を示します。この折れ曲がり角度というのは、接地面楕円の短径側の接地角度で、急角度の方です。青い点が700×25C、赤丸がETRTO406×25Cの場合です。折れ曲がり角度も小径タイヤが700Cの場合よりも大きくなります。折れ曲りが大きいということは、ゴムのヒステリシス・ループ(タイヤ損失の主要因)も深く描かれるので、転がり抵抗係数RRCもその分、大きくなるでしょう。
この折れ曲がり角度は、RRCの変化にかなりよく似たグラフのように見えますよねぇ。
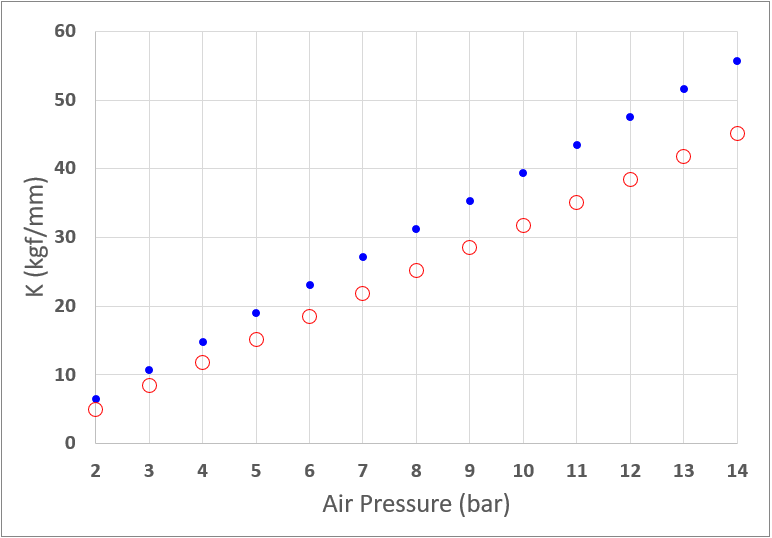
ハブ軸から見込んだ垂直剛性Kの変化
青い点が700×25C、赤丸がETRTO406×25Cの場合です。同一空気圧では小径タイヤのほうが柔らくなりますが、まあ、そりゃそうでしょう、という感じでしょうか。
空気圧とRRCの関係
さてさて、最初に引用したVittoria Corsa G+ tubular (700×25C)のタイヤ空気圧と転がり抵抗係数RRCの関係のグラフ。この推移によく似たパラメータは何か?最簡易モデルの計算結果で、Vittoria Corsa G+のグラフの推移と相関が高いパラメータを探してみます。接地面積か、凹み量か、垂直剛性か、それともトレッド折れ曲がり角度なのか??
結論を申し上げると
実測RRCと最も相関が高いのは ”タイヤトレッド折れ曲がり角度θ ” である
いきなりですが、これが本稿の結論です。
次のグラフは、Vittoria Corsa G+のRRCグラフに、タイヤトレッド折れ曲がり角度θを0.000137倍して載せたものです。結構、重なり合っていますよねぇ。つまり タイヤトレッド折れ曲がり角度θ” と転がり抵抗係数RRCの相関はかなり大、ということです。タイヤが転がって折れ曲がりがタイヤ全周にあまねく行きわたり、転がり抵抗を形成する・・・そんなイメージが湧き上がってくるような気がしますが、いかがでしょうか?
計算結果 ~タイヤ幅を変えてみる~
タイヤトレッド折れ曲がり角度θ と転がり抵抗係数RRCの相関が大、ということが窺われて、一安心。しかし、単なるナンチャッテなタイヤモデルではありますが、まだ行きます。いや~、なんだか無免許運転でクルマを運転して日本一周をしているようなヤバい気分です。
ここまでは、700×25CとETRTO406×25Cに限定して空気圧を変えてきましたが、今度は、空気圧を6barに固定して、タイヤ幅を変えて様子を見てみます。何が見えてくるのか!?
接地面形状の変化
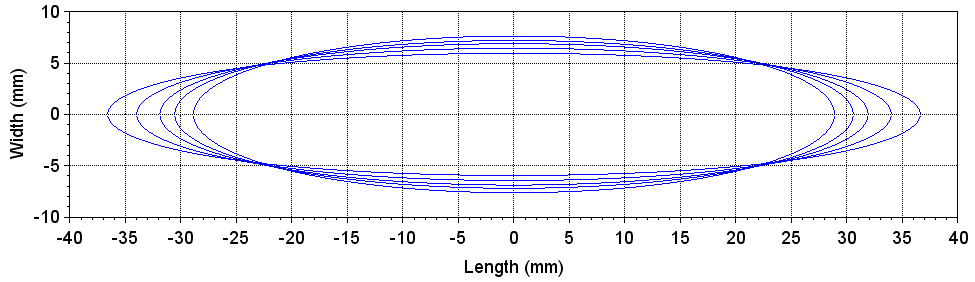
ハブ軸荷重が42.5kgf、空気圧が6barの時の、700Cタイヤの接地面形状を次に示します。なお、タイヤ幅は、19,25,32,38,48Cの5種類です。タイヤ幅が狭いほど接地面形状が細長くなります。まあ、そりゃそうなんだろうなあ、という感じです。
ETRTO 406タイヤの結果は推して知るべし。ここからは700Cに絞って話を進めます。
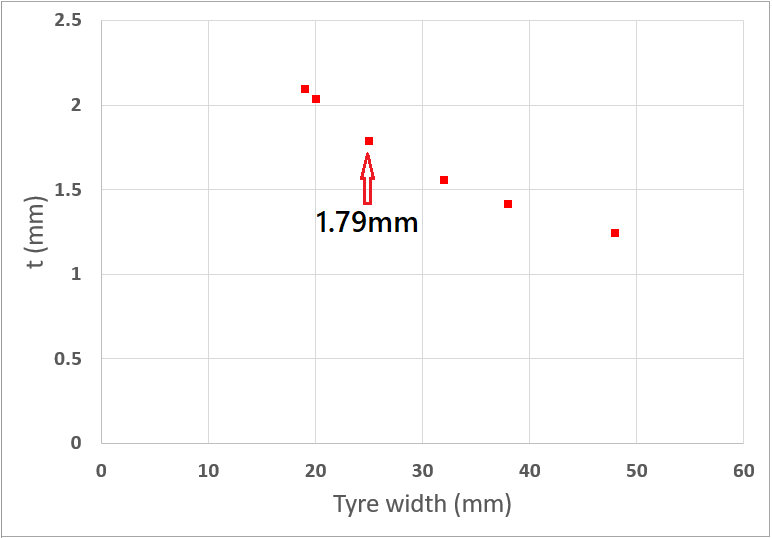
凹み量tの変化
先ほどは接地面形状の変化、今度は凹み量の変化を確認します。同様に空気圧は6barの固定で、700Cのタイヤ幅は、19,25,32,38,48Cに、ちょっと訳ありで20mmを加えた6種類です。
19mmタイヤ(今どき入手できないとは思うが)で6barでは少し凹み過ぎで、精神衛生上あまりよろしくないんだろうな、と思わせる結果です。ちなみに700×25Cタイヤに6barを与えると、t=1.79mmだけ凹んでいます。
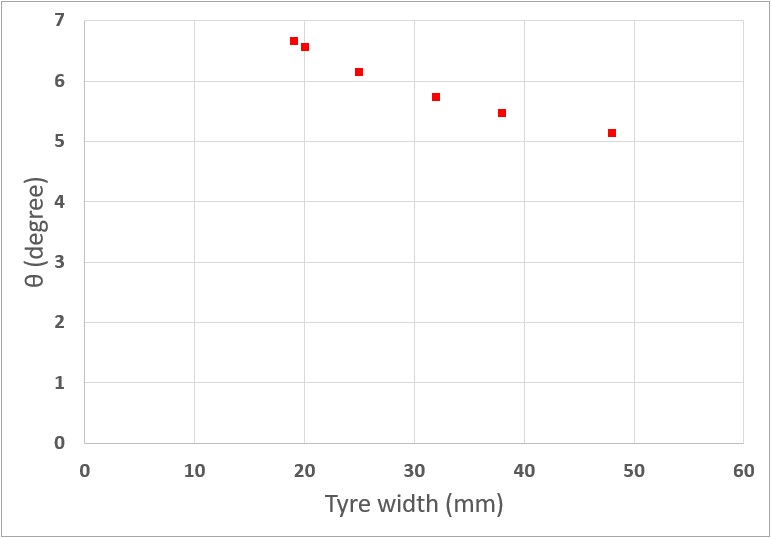
タイヤトレッド折れ曲がり角度θの変化
”タイヤトレッド折れ曲がり角度θ” の変化を示します。同一空気圧だと細タイヤは転がりが悪いのかな?と思わせるグラフです。
ハブ軸から見込んだ垂直剛性Kの変化
次のグラフは、空気圧一定でタイヤ幅を大きくするとタイヤが「硬く」なるということを示しています。太いタイヤに思いっきり空気を入れて高圧にすると、ものすごく硬くなるわけです。しかし、48Cタイヤに6barもいれる人はいないので、このグラフはなんだかなあ、ではありますが。
となると・・・例えば、タイヤ凹み量とタイヤ幅の比率が同一になるように空気を入れる、というのはどうでしょうか?20mm幅タイヤで2mmだけ凹むのなら、それじゃ、40mmタイヤは4mmだけ凹むとイイ感じじゃねえか?という単なる思い付き、です。
タイヤ凹み量とタイヤ幅の比率が同一になるように空気圧を設定する
先ほどの結果で、700×25Cタイヤに6barを与えると、t=1.79mmだけ凹みましたが、今度は、20C,25C,32C,38C,48Cで、すべてについて、凹み量とタイヤ幅の比率が同じ値になるように空気圧を設定してみました。
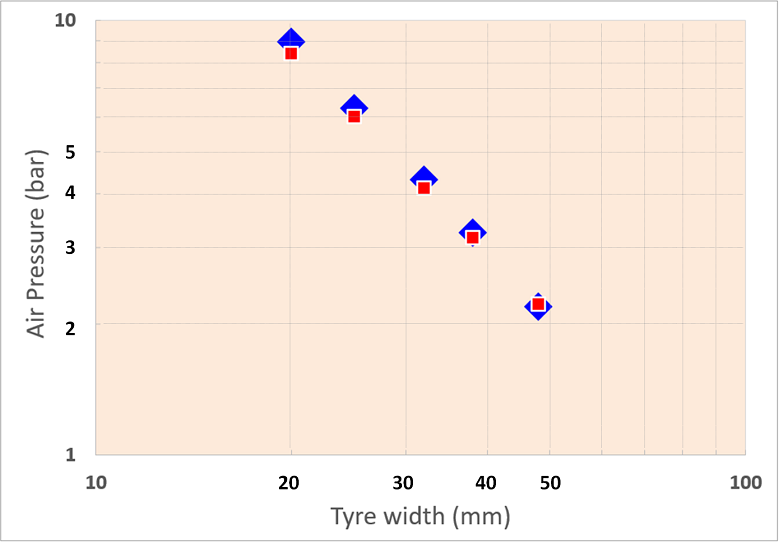
すると、次のグラフの赤■のようになりました。このグラフは、これまでとは違って、対数表示としています。タイヤ幅と空気圧の両方を対数表示とすることで、直線に乗るような結果となっています。赤■で、25Cが6barですが、48Cは2.22barとなります。太いタイヤは結構な低圧で使う方も多いので、まあ、そんなものかな?という数値ではあります。
さて、赤■の背後にうごめくデカくて青い◆は一体、何者なのか?
これは、実は、CBN本館のレビューでも取り上げられた空気圧計算のWebサービス “Silca Professional Pressure Calculator” に私の体重などの数値を当てはめて、各タイヤ幅で計算した空気圧です。
赤と青が何だか同じ直線上に乗っているように見えますが、それはタマタマ。ここで注目すべきは、2つのデータ系列の直線の傾きが、ほぼ同一である、ということです。つまり、
もし、本稿で扱ったナンチャッテ簡易モデルがある程度正しいとすれば、SILCAの空気圧計算機は、タイヤ凹み量とタイヤ幅の比率が同一になるようなルールに基づいて空気圧を設定しているのではないか?と推測される
ということです。
「なーんだ、ナンチャッテが正しい場合には、かよ」
まあ、そこがちょっとアレなんですが、意外とイイ線いってるかもしれませんよ。SILCAの中の人、教えてくれないかなぁ。
そのとき、垂直剛性Kはどうなるか
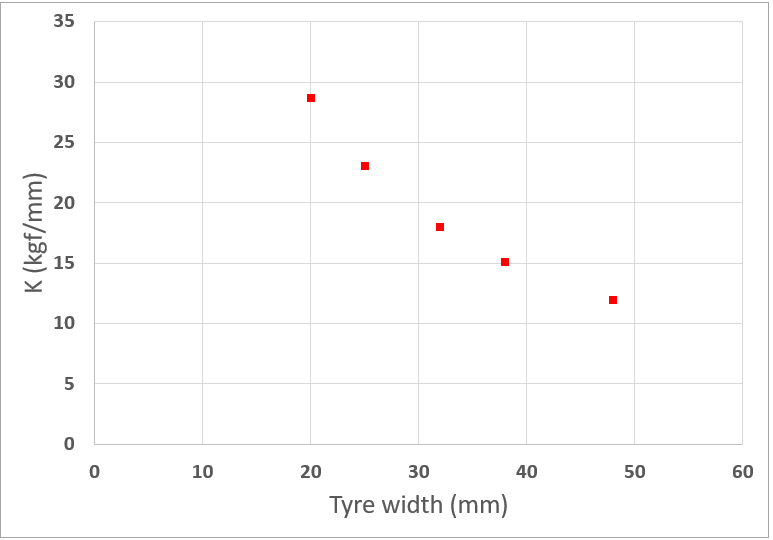
では、タイヤ凹み量とタイヤ幅の比率が同一になるように空気圧を設定すると、タイヤの垂直剛性はどうなるでしょうか。計算結果を次に示します。
なるほど、太いタイヤは柔らかい。これはいわゆる、乗り心地がマイルドってやつですね。でもこの設定ではRRCが悪くなるのではないか?心配です。
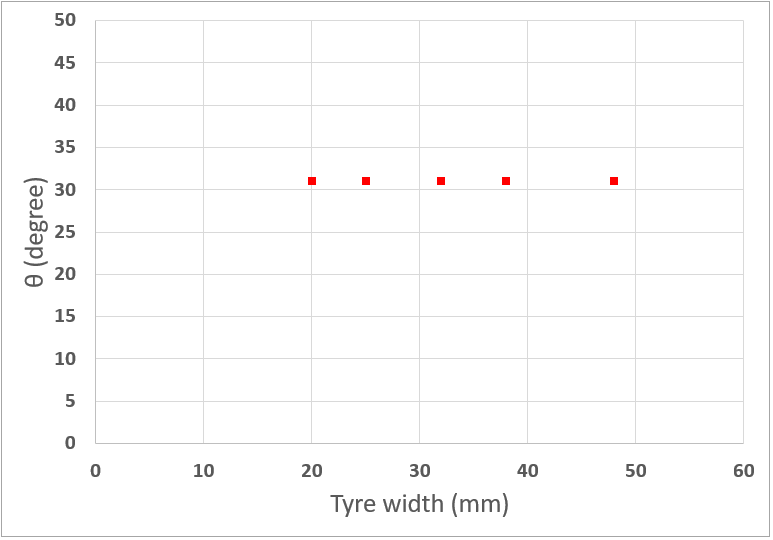
そのとき、RRCと相関の高いタイヤトレッド折れ角度θはどうなっているのか
タイヤ凹み量とタイヤ幅の比率が同一になっているのですから、当然ですが、すべてのタイヤで同じ折れ角度になります。
そういえば、本稿の結論は、
実測RRCと最も相関が高いのは ”タイヤトレッド折れ曲がり角度θ ” である
でした。ということは、上のグラフは、タイヤ凹み量とタイヤ幅の比率が同一になる空気圧を設定すれば、タイヤ幅に関係ない、RRCは同じような数値を示す、ということなのでしょうか!
いいえ、残念ながら違うでしょう。トレッドの折れ曲がりがタイヤの転がり抵抗を引き起こす主犯であるならば、同一折れ曲がり角度では、タイヤ幅が大きい方が、折れ曲がりを示す長さがその分、長くなります。
なぜなら、タイヤ幅が大きいほど空気圧を低く設定しており、したがって接地面積が増大し、面積を形成する長円の周長も大きくなるからです。したがって、RRCは接地面積の平方根に比例する、または空気圧の平方根の逆数に比例する、と考えるべきです。
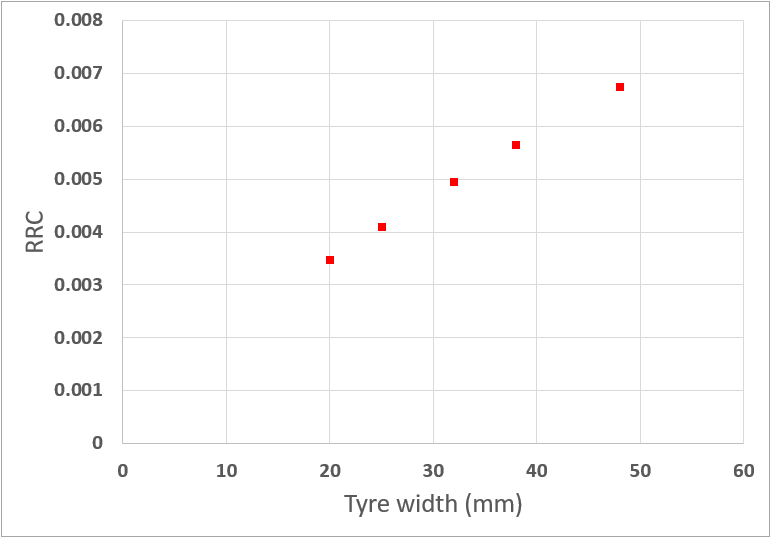
そんな風に考えて、25CのRRCを基準として、各サイズのタイヤのRRCを描いてみると、次にようになります。最初に示したVittoria Corsa G+ tubular (700×25C)の6barにおけるRRC実測値として、0.0041を読み取ることができますが、この数値を基準として、描いてみます。
このRRCと、先ほどの垂直剛性Kの関係ですが、Kはタイヤ幅増大とともにかなりの勢いで低下しています。一方で、RRCは増加します。
つまり、“タイヤ凹み量とタイヤ幅の比率が同一になる空気圧を設定する”というやりかたは、どちらかというと大径タイヤで、より乗り心地方向に振った特性が得られ、細タイヤではより転がり抵抗低減方向に振った特性が得られる空気圧設定である、ということができます。
で、SILCAの空気圧計算機ですが、これはもしかして、大径タイヤは乗り心地重視、細タイヤは転がり抵抗低減重視になるような空気圧を与えるように色付けされているのではないか?と推測することができます。
で、実際の運用に際しては、自分の好みに合わせて空気圧を上下させればよいわけですが、太いタイヤの場合、SILCAの計算結果よりも低圧で使っている方はたくさんおられると思います。太いタイヤの良いところは、低圧でもタイヤのキャパシティ(凹み余裕)が大きく、安心して乗れる、とか、低圧化して垂直剛性を低く設定できるので、荒れた路面での食いつき、スタビリティが高くなるなどがありますが、日本の道路の路面状況事情の好転が今後、あまり望めず、また、グラヴェル路走行嗜好への流れを考えると、細いタイヤがあまり使われなくなるのは必然かも知れません。
そして、例の素晴らしきRRC実測サイト
例のRRC実測サイト。実は興味深い記事が存在します。
参考 Continental Grand Prix 5000 Comparison: 23, 25, 28, and 32 mm Compared
このサイトでは、同一銘柄で幅違いのそれぞれの推奨空気圧設定を、タイヤ幅に対して、同じある比率で凹む場合の空気圧として規定して比較試験しているようです。というわけで、私が気分ででっち上げた “タイヤ凹み量とタイヤ幅の比率が同一になるように空気圧を設定する” というルールは、実は結構、普遍的な考え方で、SILCAもそれを踏襲しているのではないか?などと思ってしまうわけです。
で、上に挙げた興味深い記事には、さらに面白いことが書かれていますが、本稿では触れないことにします。是非、ご一読を!!
ちょっと待て、接地面形状の実際はどうなっているんだ?
師B 「おい、実際のタイヤの接地面形状は確認したのか?」
宅浪 「そりゃ面倒ですよ」
師B 「ヘッ、ヴァーチャルで何がわかるんだよ・・・フフフ」
というわけで、実際にタイヤの接地面形状を確認してみましたので、最後にそれを示します。マドガード付きのクロスバイクで使っているコンチネンタルのULTRA SPORT 700×28Cで、幅の実測値は29.5mm、雨天走行がやたらと多い2900km走行後のリアタイヤです。
次の図で、赤い魚拓みたいなヤツが実際の接地面を紙上に転写したものです。タイヤにスタンプ用インクをベタベタと塗り、紙の上にリアタイヤを置いて、そ~~っと乗車して取った接地面魚拓です。その後、体重計を置いてリア荷重をみると、魚拓に集中するあまり、思いっきり後ろ乗りしすぎて55kgfほどの荷重がかかっていたようです。なお、青い実線は、幅29.5mm、軸荷重55kgfで計算した結果です。
軸荷重推定値はあまり正確ではないので、魚拓の大きさと、同じ条件で計算した青実線の大きさを有意に比較するのは難しいですが、いずれにしても、実際の魚拓の方が細長くなりました。これは、実物では、タイヤトレッド自体の曲げ剛性が加わり、中央部の接地面圧が周縁部よりも高い、というのが主要因だと思われます。特に前後端は接圧が低く、しかし、触ってしまえばしっかり魚拓として記録されてしまう、というあたりでしょうか。それに、魚拓を取るのが結構、難しい。
さて、本当はどういうからくりで、この差が生じるのでしょうか?理由はいろいろ考えられますが、じっくり考えてみるのも面白いでしょう。
まとめ
- タイヤを細長いドーナツのように見立て、このドーナツをスパッと切り落として現れる楕円形風の面をタイヤの接地面形状と見做すよう超簡易的なタイヤ変形モデルを採用し、実測RRCと最も相関が高いのは ”タイヤトレッド折れ曲がり角度θ ”であると推論したが、これはトレッドを深く折り曲げると損失も大きくなるというイメージと一致する
- SILCAのWebサービスである “Silca Professional Pressure Calculator” は、タイヤ凹み量とタイヤ幅の比率が同一になるようなルールに基づいて空気圧を設定していると推測した
- このルールに基づく場合、タイヤ幅増大とともにRRC(転がり抵抗)も増大し、一方で垂直剛性(タイヤの硬さ)は低下すると推定されるが、ユーザーは、RRCと垂直剛性のバランスを勘案し、自分の嗜好を反映させた空気圧設定を行えばよい
- つまり、自分の感覚を研ぎ澄ませて、それを信じて空気を入れるべし!(えーっ、結局そこかよ!!)