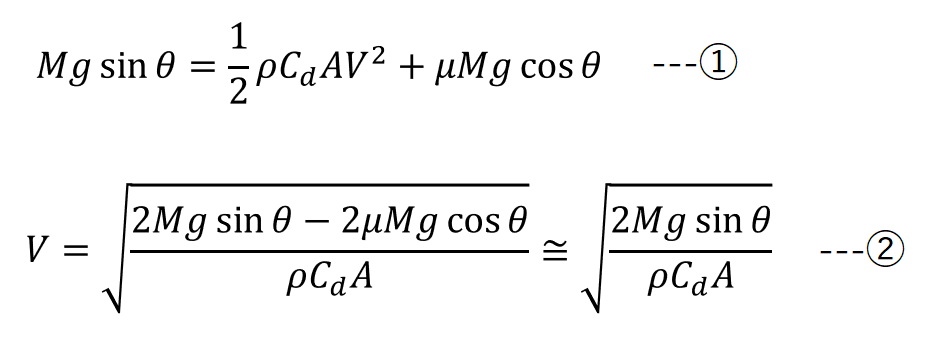近所のおじさん(以下敬称略オヤジ):惰性で坂を下ると、やがて自転車は?
宅浪:そりゃー、だんだん上がるでしょ、スピードが。
オヤジ:なぜか。
宅浪:下り坂だから?
オヤジ:それは正解だ。
宅浪:ですよねぇ!(へへっ、チョロいオヤジだぜ・・・)
かつて、下り番長で鳴らしたと自称する近所のオヤジの下り坂放談に付き合って、めまいがしてしまった。というわけで今日は、その顛末を再現しようと思う。テーマはズバリ、「終端速度」なのだっ!
(番長って・・・古っ)
終端速度ってなんだ
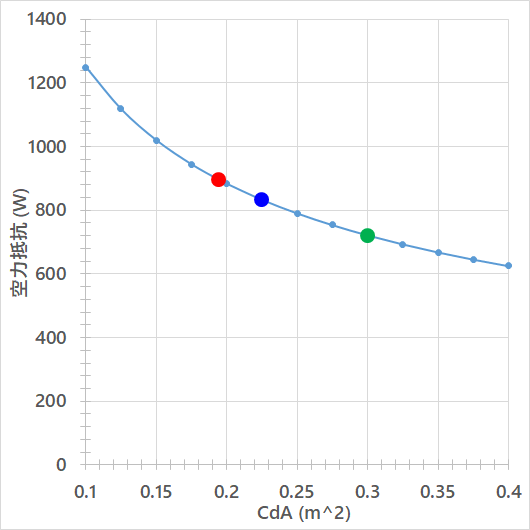
オヤジ:これ見るべし。
宅浪:なんだこれ、シーデーエー? 終端速度?
オヤジ:終端速度ってのは、下り坂で惰性走行したときに近づく最高速度のことさ。
宅浪:あー。
オヤジ:一定勾配の長い下りでは、時間とともに終端速度に近づく。
宅浪:そりゃそうだろな。
オヤジ:がむしゃらに回して終端速度に持ち込み、あとはダウンヒルポジションでそのまま下る、とかね。
宅浪:んで、シーデーエーって、空力だよね?
オヤジ:そう。その数値が小さいほど受ける空気抵抗が小さい。CdAはCdとAで出来ている。
宅浪:あ、そうなんだ。
オヤジ:が、細かいことは気にしない。
宅浪:オイラ気にしないよ。で、赤青緑のデカ丸って何よ?
オヤジ:赤のCdAは0.194、青は0225だけど、実はこれ、CBN Blogで紹介されていたSwiss Sideの記事から引用したんだ。
宅浪:ほっほぉー。

オヤジ:この引用先に、トップチューブ座り(スーパータック:super tuck)のダウンヒルと、ノーマルなサドル座りのダウンヒルの時のCdAの値、つまりさっきの2つの数値0.194と0225が定義されているんだ。
宅浪:へー。
オヤジ:上のグラフはそのCdA値を使って終端速度を計算してみた結果だよ。
宅浪:ふーん。
オヤジ:このSwiss Sideの記事は詳細が省略されているので想像するしかないんだが、画像を見ると、んー、160センチで54kg位かな~?の女子ライダーで風洞計測しているらしく、2つの数値はその結果と見た。
宅浪:なにその眼力。もう少し身長あるようにも見えるけど、ま、いいや。で、それがどうかしたわけ?
オヤジ:CdAが0.194というのは、その女子ライダーの体格の場合の数値なんだ。185センチもあるようなデカい選手にこの小さい数値はちょっと窮屈すぎ。
宅浪:つまり、さっきのグラフはその女子ライダーに固有の結果ってこと?
オヤジ:そうさ。
宅浪:いや~、オレそんなこと全く気付かないっていうか、普通、そんな深読みしないよ。
オヤジ:グラフは下り勾配8%の時の結果なんだが、赤丸のスーパータックの終端速度が71.5km/hで、青丸のサドル座りは66.3km/hだ。
宅浪:うっ、4.2km/hも差があるわけ? このまま10km下ったら、えーと・・・
オヤジ:39秒の差がつく。
宅浪:そりゃすげぇな。で、緑のデカ丸は?
オヤジ:緑はCdAが0.325だけど、まあ、趣味でロードに乗っている人の下り空力はこのあたりかな、とオレが勝手に決めちゃったってわけよ。サドル座りで普通に下るって感じ。
宅浪:趣味の人は57.5km/hですか。
オヤジ:宅浪もそのあたりだよ、きっと。
宅浪:ん-、オイラもう少し速度出るような気がするよ。
オヤジ:たしかに宅浪はデカくて重い分、もう少し出そうだな。
宅浪:ところでCdAが小さくて空力がいいと、終端速度が大きくなるけど、その時の空力抵抗パワー(ワット)は変わらないんスよね?
オヤジ:そんな風に想像する気持ちはわからなくもないけど、違うんだなー、コレが。
宅浪:ええっ??
終端速度における空力抵抗パワー
オヤジ:こんなふうになるよ。
宅浪:ん?さっきのグラフと全く同じじゃね??
オヤジ:形はそっくりだが、縦軸が空力抵抗で単位がワットになってるよ。
宅浪:あホントだ。CdAが小さいと速度が上がって、ううーむ、空力抵抗(W)が増してる!ど、どーゆーことですかコレわーっ!!
オヤジ:血圧下げろ、宅浪。
宅浪:はー、ふぅ~。
オヤジ:まず、下り勾配でCdAが小さいと終端速度が上がるわな。すると、1秒間で下る標高差も大きくなる。
宅浪:標高差? ん、まあ、そりゃそうだ。
オヤジ:終端速度ってのは、実は地球の仕事の結果なのさ。
宅浪:し、仕事?なんだよそれ。
オヤジ:例えば時速72km/h、つまり秒速20m/sで10%勾配を下ったとする。1秒間で下る標高差は?
宅浪:1秒間で20メートルだけ進んで、その間に10%勾配分だけ標高が低くなると考えると、2メートルじゃねえの?
オヤジ:正確には1.993メートルだが、そこはこだわる必要はない。2メートルだ。
宅浪:その2メートルが何だっての?
オヤジ:自転車を抱えて2メートルの塀の上から下に飛び降りてみたら、スゴい衝撃だよな?
宅浪:わっ!痛すぎて、泣く。
オヤジ:つまり、地球が2メートル分のエネルギーを宅浪と自転車に与えたから、その衝撃を感じたわけだ。
宅浪:ほほー。
オヤジ:10%勾配を時速72km/hで下ったとすると、毎秒2メートルずつ標高が下がるから、1秒ごとに、その衝撃分のエネルギーを地球から繰り返しいただいてるってことさ。
宅浪:えーっ、1秒ごとに2メートルの塀から繰り返し飛び降りてるのか!?
オヤジ:そう。
宅浪:もうオイラは満身創痍じゃねえか!そんな強力なエネルギーで終端速度に導かれるってわけか。
オヤジ:そうさ。しかも、空力がいいと、余計にスピードが出る。
宅浪:ま、そこは、当然じゃね?
オヤジ:だろ?で、スピードが出ると、1秒間に低くなる標高差は?
宅浪:大きくなる。
オヤジ:ただそれだけのことだ。
宅浪:・・・あれっ・・・空力がいいと、地球からいただくエネルギーも勝手に増える?
オヤジ:そうさ。
宅浪:おーっ、下り坂の神秘か。
オヤジ:そのエネルギーは、空力抵抗と転がり抵抗の合計と釣り合う。
宅浪:はほー。
オヤジ:時速72km/hでは空力抵抗が大半だから、空力抵抗と釣り合う、と言ってもいいかもしれないね。
宅浪:あれーっ!なんかわかった気がするぞ、オヤジっ!?
オヤジ:何となくわかれば、それでいいのさ。なーんにも考えずに乗った方が自転車は楽しいからな。
宅浪:そっ、そーだよね!
宅浪:そういえば気になるのが、フランスやイタリアの山岳ダウンヒルなんかで、時速100km/h!!とか言ってるけど、あれ、実話?
空気が薄いとスピードが出る
オヤジ:標高が高いってこともあって、それは本当に出ていると思うよ。中継で追走する二輪の速度計がマジで100km/hを指してたりするのを見たことあるからな。
宅浪:カメラ担いでる後ろの人、大した度胸じゃね?
オヤジ:しかも現代のレースではベルナール・イノーの時代より明らかに下り速度が上がっていると思うな。今のトッププロの中にはマジで下りを攻める選手が少なからずいる。
宅浪:こわいよぉ。下りの中継見たくない。
オヤジ:オレもすっかり苦手になった。2003年だったか、ホセバ・ベロキの大落車をテレビで見て以来、ツールから疎遠になっちゃったもんね。
宅浪:うわ~。
オヤジ:最近すっかり観てないけど110km/hとか出ることあるんじゃ?
宅浪:ぐぉ~~っ、遠慮したい世界だ。
オヤジ:同じ下り勾配でも、2000m級山岳の下りと、ジャパンカップの古賀志林道の300m級の下りでは、明らかに終端速度は変わってくるだろうな。
宅浪:ふ~ん。
オヤジ:ところでクリス・フルームに代表されるスーパータックだけど、1990年代はあのカンピオーネ、マルコ・パンターニのポジションがサイコーにカッコよかった。
宅浪:へぇ~~~。
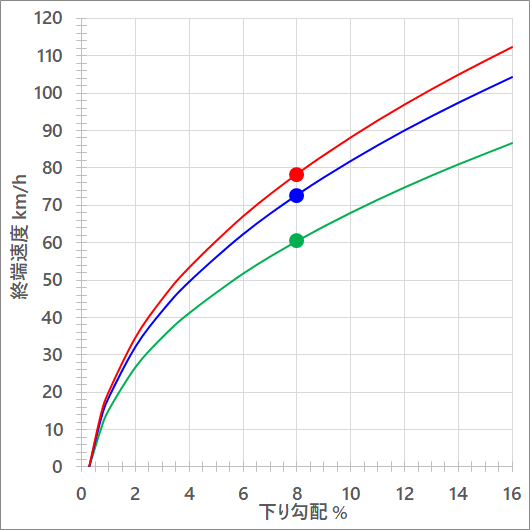
宅浪:で、例えば標高2000mで8%の下り勾配の終端速度は具体的にいくつになるわけ?
オヤジ:こうなる。赤青緑はそれぞれスーパータック、ノーマル、趣味ロードで、前のヤツと同じ。
宅浪:おっ、すげぇ、いろんな勾配の結果が!んで、デカ丸のところが8%勾配か。
オヤジ:スーパータックは78.3km/hだな。最初のグラフは71.5km/hだったから、6.8km/hも違う。
宅浪:ってことは10km下ったら、44秒も差がつく!
オヤジ:コレ、例の女子ライダーのCdAの結果だから、大型選手ならもう少しスピード出るよ。
宅浪:あれっ?ところで最初のグラフの標高はいくつだったんだ?
オヤジ:あっ、言い忘れてたが、最初のヤツは標高107mで気温が21.5℃だ。
宅浪:ハンパな標高だなぁ。ってか、気温も半端じゃん?
オヤジ:標高が高いと気圧が低い。つまり空気が薄い。気温が高いと空気が膨張して同じく、薄くなる。
宅浪:あー、空気が薄いと空気抵抗が減るってわけね。
オヤジ:そうそう。
宅浪:なわけで、終端速度には標高に加えて気温も影響するってことなんかいな??
オヤジ:そう。107mで21.5℃だったとする。そこから2000mまで上ると、気温が100m毎に0.6℃程度下がるから、上のグラフはそれを加味して2000m地点では10.1℃で計算しているんだ。
宅浪:なんだオヤジ、芸が細かいんだよ!まあしかし、勾配16%で110km/h超えるのか。恐怖でしかない。
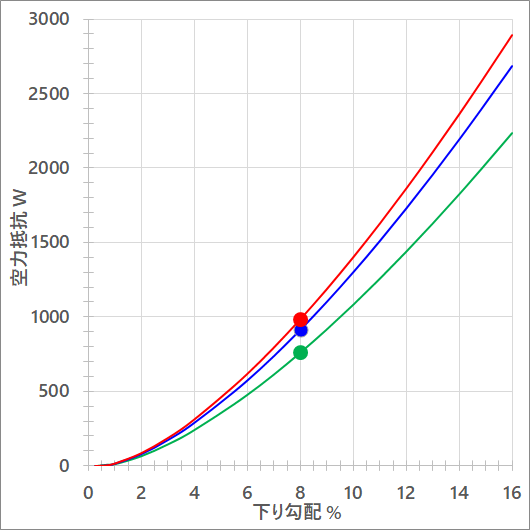
オヤジ:速度だけじゃアレだから、ついでにその時の空力抵抗パワーも示しておくよ。
宅浪:わっ、何だ、このうなぎのぼり感は!
オヤジ:いや実は、空力抵抗パワーは速度の3乗に比例するもんでねぇ。フフフ・・・
宅浪:フフフじゃねえって。2900ワットとか、聞いたことない数字だぞっ!!
オヤジ:ま、オレはもうすぐ 「人生下り坂、最高!」 のお歳頃だし、ゆ~っくりと季節を感じながら下ることにしてるよ。
宅浪:そういう話じゃないって。
足りない何か、とは
オヤジ:で、あのさ、何か足りないと思わねぇかい?
宅浪:はっ、へっ?
オヤジ:実は、終端速度は下り勾配、CdA、標高、温度だけでは決まらないんだよ。
宅浪:え、まだなんかあるんか?
オヤジ:タイヤの転がり抵抗が大きいと、終端速度は小さくなる。
宅浪:そ、そんなのは当たり前じゃないか!
オヤジ:ここまでの計算では、転がり抵抗係数を、一般的な路面と現代的なロードタイヤの組み合わせとして、0.0054に設定してある。
宅浪:へぇ~。
オヤジ:終端速度を決めるファクターが実はほかにもある。
宅浪:えっ、まだあるんか?もうやめてぇ~~。
オヤジ:重さだよ。人と自転車を合わせた重量。今頃いうのもアレだが、ここまでの計算では、160cmで54kgのライダーと、ウエア+自転車の重さとして8kgを想定している。
宅浪:あー。だからデカい選手はスピード出るって言ってたわけね?重いほうがスピード出そうな気がするわな。2mの塀から飛び降りたら重い方が衝撃デカいし。
オヤジ:何だかすっかり分かった気になったよなぁ、宅浪!
宅浪:わ、分かった気になったってことが大事っスよねぇ??
欧州の大型選手と下りで互角に勝負するには
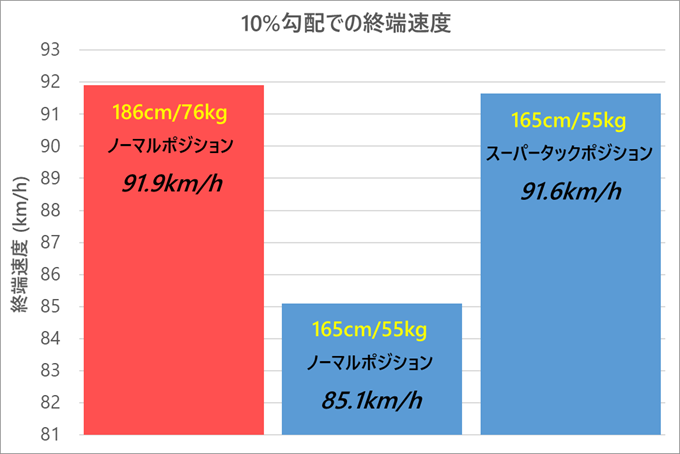
オヤジ:さて、例えば186センチで76kgの大型選手と、165センチで55㎏の小柄な選手で考えてみる。
宅浪:今度は男子ライダーで揃えたってか?
オヤジ:標高2000mの10%勾配をノーマルポジションで下ったら、終端速度はどうなるかな?
宅浪:デカい選手は重いから下りは速そうだな。でも風を受ける面積も大きいからCdAは良くないはずだ。どうなるんだ!?
オヤジ:そこが面倒なんだ。CdAは身長と体重のちょっと複雑な関数になる。そこは採用する数式モデルで差が出るところだが、オレが採用したモデルを適用した計算結果がコレ。
宅浪:ムムッ?デカい選手はノーマルポジションで91.9km/hだが、小柄な選手は85.1km/hか。
オヤジ:この終端速度に甘んじて10kmの距離を下れば、大きい選手は6分32秒で下りきるが、小柄な選手は7分3秒だ。
宅浪:下りきった時点で31秒の差がついてしまうのか!
オヤジ:だが、ここで小柄な選手がスーパータック・ポジションで下ると、ほとんど差がつかなくなる、ってのが、このグラフが言ってることだ。
宅浪:おおおーっ!!
オヤジ:でも、UCIルール変更でスーパータックが禁止になるらしいんだな。
宅浪:あそうだ、最高地点で中実鉄フレームの超重量級マシンに乗り換えて下ればいいんだ!
オヤジ:なるほどねぇ。
宅浪:それにしても小柄な選手は下りで苦労するってことなのかなぁ。
オヤジ:軽量だったマルコ・パンターニは、偉大なクライマーだったが、あのパンターニ・ポジションの降坂技術があったからこそ、大型選手と互角に戦えたってことかもねぇ。
宅浪:マルコ・パンターニか・・・
この先、余興につき
宅浪:余興ってなんスか?
オヤジ:せっかくだから、一応、式を書いておくよ。
宅浪:うわっ、チョー睡魔。。。
オヤジ:上の式①だけど、左辺は、地球が下り勾配進行方向に引っ張ってくれる力。Mは自転車と人の総質量で、例えば72kgとかとか。gは重力加速度で9.8m/s^2。
宅浪:θが勾配かいな?平坦路では左辺がゼロね?
オヤジ:sinθは、勾配8%の場合は、100で割って0.08でいいよ。ホントはちょっと違うんだけど。すると、左辺はいくつになる?
宅浪:72×9.8×0.08=56.45
オヤジ:その単位はN(ニュートン)っていうんだ。
宅浪:しってる。
オヤジ:式①の右辺だけど、ひとつ目が空力抵抗で、ふたつ目が転がり抵抗だ。
宅浪:空力と転がり、か。
オヤジ:式②は式①から終端速度Vを解いたものだが、簡略化した一番右の式は、ダウンヒルでは空力抵抗が支配的なので、転がり抵抗を無視しているってわけだ。
宅浪:えっ、そんな強引なことやっちゃっていいのか!
オヤジ:大きな傾向を掴むのが大事だからね。
宅浪:なるほど。
オヤジ:式のかたちをじ~~っと眺めれば、何がどんなふうに終端速度に効いてくるのか、わかってくるってものさ!
宅浪:はほへぇ~。
オヤジ:式①右辺のひとつ目の式。ρが空気密度なんだが、これは標高100mで25℃の平凡な数値として1立方メートル当たり1.2kg、つまり1.2kg/m^3としておこう。で、CdAは例のヤツで、ノーマルポジションの0.225m^2としてみよう。
宅浪:ここまでの数字をまさか式②に入れるってか?
オヤジ:一番右の式に、どうぞ!
宅浪:V=√(2×72×9.8×0.08)/√(1.2×0.225)=20.4・・・あれっ、遅いじゃん!?
オヤジ:その速度は秒速だよ。時速にするには3.6を掛けるべし。
宅浪:イケネ・・・あっ、73.6km/hってなったぞ。キター、もっともらしい~~。
オヤジ:式②の一番右の式は転がり抵抗を無視しているってこと、忘れないでくれよッ!ちなみにμは転がり抵抗係数で、0.0054とかだけどな。
宅浪:ふむ・・・。
人間は考える葦である
オヤジ:「人間はひとくきの葦にすぎない。自然の中で最も弱いものである。だが、それは考える葦である。」
宅浪:はっ?なんで足が考えるわけ?
オヤジ:宅浪。とにかく結果だけを求めるのが今の時代の風潮さ。考えているふりはするけどな。
宅浪:あー、オイラも問題集はすぐに解答を見ちゃう方だな。考えるの面倒だし。
オヤジ:そのホイールは速いのか、そのペダリングは効果があるのか、疲労しにくいサプリはどれなのか、簡単な能書きと結果だけ手っ取り早く教えてくれ!ってな。
宅浪:へへへっ。
オヤジ:考えるって、本当は面白いんだぜ。下りも登りも、考えれば考えるほど面白い。だが、自転車に乗っているときは、「考えるな、感じろ」 かなー。危ないし。
宅浪:なんか知らんけど、オヤジ、わ、わかったような気がするよ、下りの神秘が!!
・・・
と、日記には書いておこう。
なお、この放談はフィクションであり、登場するオヤジと宅浪は実在の人物とは無関係です。