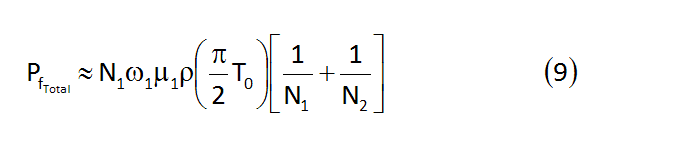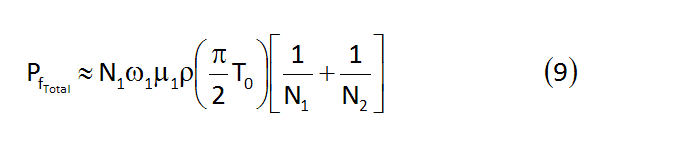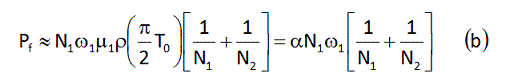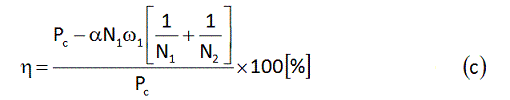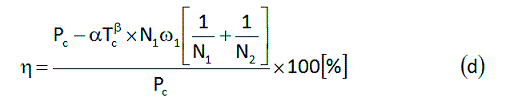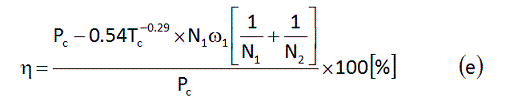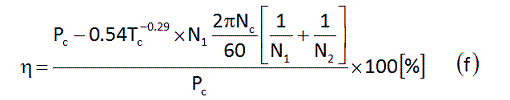いつもお世話になっている自動車整備工場の百戦錬磨技師Aさんいわく
師A 「クルマのエンジンから駆動力を取り出すのがトランスミッション」
宅浪 「はぁ」
師A 「トランスミッションの中にはギヤがたくさん入ってる」
宅浪 「ほぉ」
師A 「1組のギヤの伝達効率は98.5%ほどかな」
宅浪 「へぇ」
師A 「2枚の歯車をチェーンでつなげると効率はどうなるか」
宅浪 「かみ合わせが2カ所になるから98.5%の2乗で97%?」
師A 「ヘッ、どうかな・・・フフフ」
なに勿体ぶってるんだ。こっちは自転車通勤百戦錬磨だぜ。
どうでもいい対抗心を燃やしつつ、宅浪はチェーンの伝達効率が気になって仕方がなかった。
チェーンという便利すぎる伝達媒体
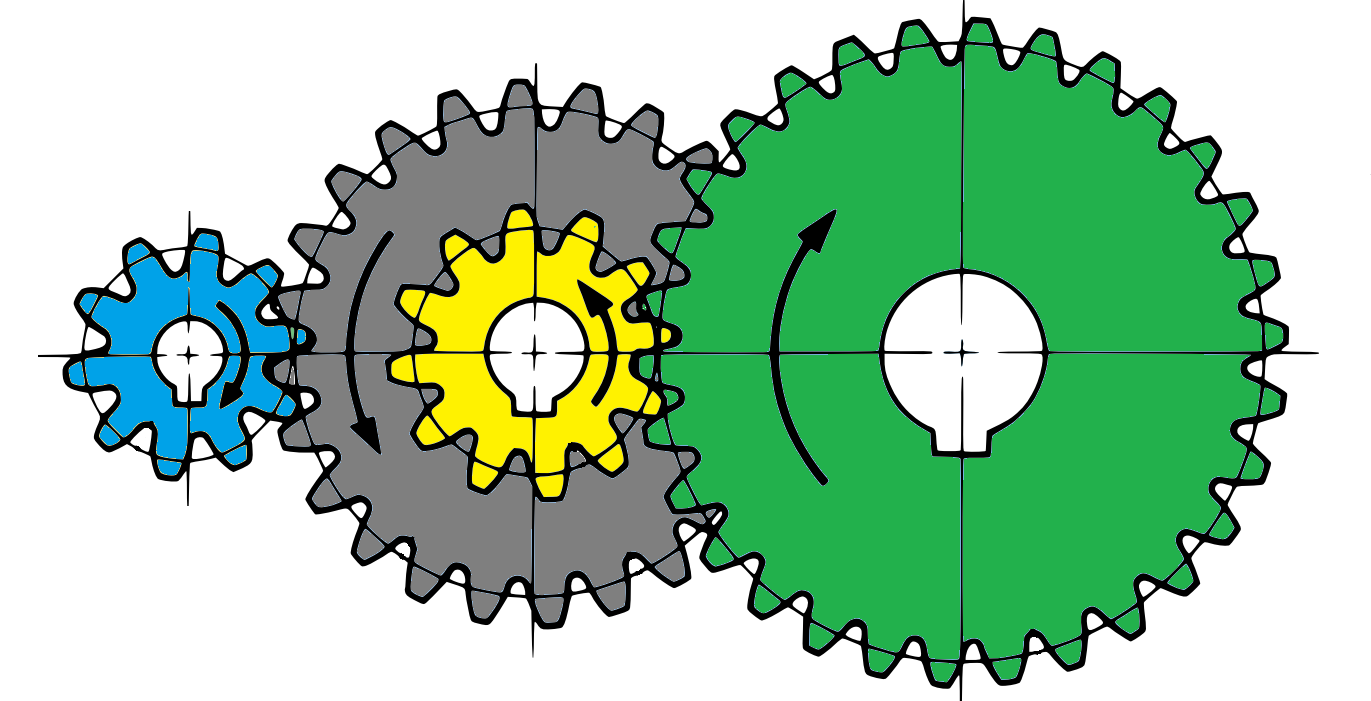
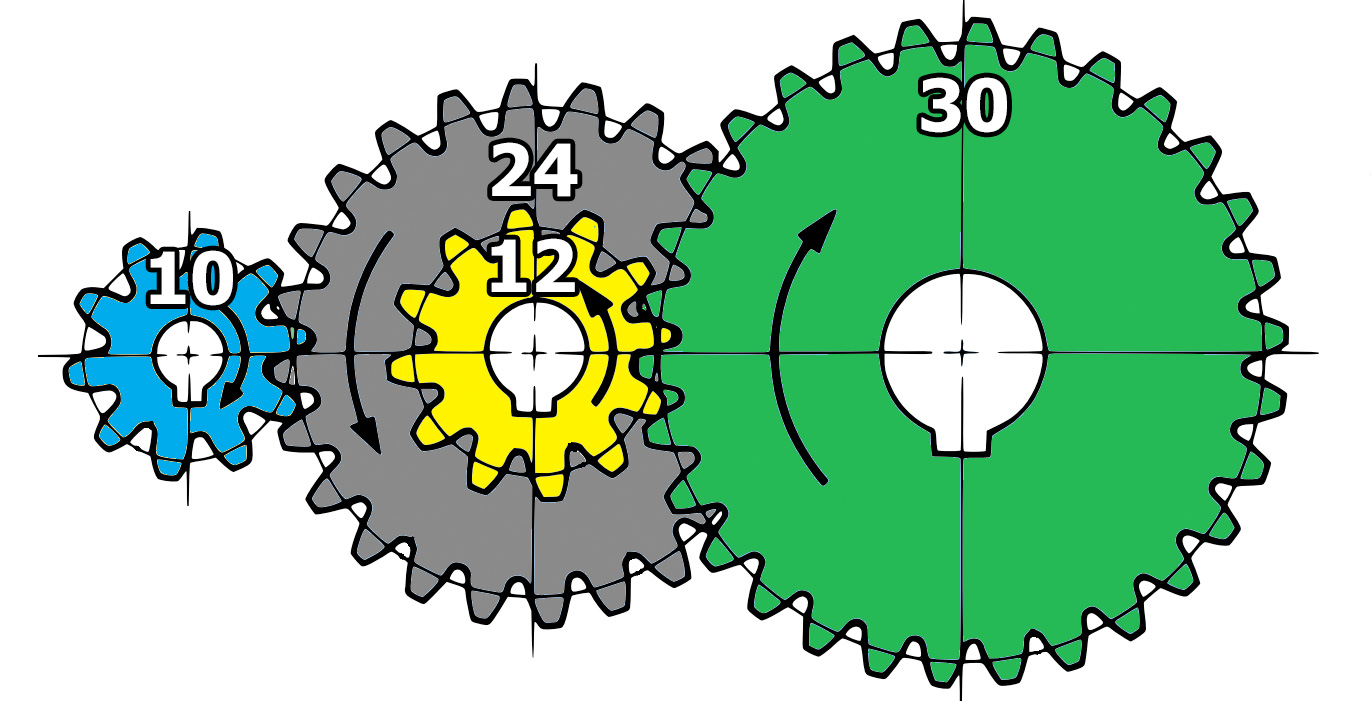
ギヤの図をご覧ください。
- 右側の緑色の大ギヤの歯数が30
- 真ん中の2枚一体ギヤは、黄色が12でグレーが24
- 左側の青い小ギヤが10
この場合、緑の大ギヤから青の小ギヤへの増速レシオRは、
R = 30/12 × 24/10 = 6
です。
自転車でいえばこれは、トップ×アウターのレシオみたいなものでしょう(ちょっと値がデカすぎですが)。例えばスプロケ9Tに対してチェーンリング54T。緑の大ギヤと青の小ギヤの間をつなぐのが2枚重ねの中間ギヤですが、自転車のチェーンというのは、この中間ギヤと同じように前後ギヤをつないでいます。
まさか自転車にこういうギヤのみの伝達機構を使うなどという発想は、チェーンが当たり前と思っている私には到底できません。リアセンターの長さの調整が楽になるし、容易に多段化を実現することが可能になるなど、チェーンというのは実に便利ですよねぇ。
禁断の世界へ
チェーン潤滑剤という商品ジャンルがあります。様々な潤滑剤が存在し、様々な効能が主張されています。注目度も高いし、定期的に雑誌でも取り上げられます。潤滑剤の役割は、
- チェーンの長寿命化
- チェーンーギヤ間のパワー伝達損失の低減
- 長距離ライドへの対応
- 静穏化
といったところでしょうか。特に1)チェーンの長寿命化 が重要です。チェーンは、次の画像のようにピン、ブッシュ、ローラー、内外プレートにより構成されていますが、ピンは外プレートに、ブッシュは内プレートにそれぞれ固定されるため、チェーンとギヤが噛み合うときに、ピンとブッシュは常に同じ位置関係で摺動し、同じ部分が摩耗するため、チェーンの伸びに極めて大きく関係します。
したがって、最も潤滑剤を必要とするのがピンとブッシュの非常に狭い隙間ということになります。ここに浸透しなければ長寿命化は不可能です。(※余談ですが、画像上段のチェーンはKMCの11速チェーンX11SL、下のチェーンはサンツアーの7速チェーンULTRA-6で、40年ほど前の製品。KMC X11は1/2×2.75/32インチで9速以降の薄歯に対応し、ULTRA-6は1/2×3/32インチで、8速までの厚歯に対応します。)
ところで、潤滑剤云々以前に、そもそもギヤーチェーン系の伝達効率はいかほどなのでしょうか。
チェーンの性能を引き出すためのチェーン潤滑剤という商品は注目度が高いし、売り上げも結構な額になっていると思われます。ところが肝心のチェーン伝達効率そのものは、その重要性の割に注目度が低いと思いませんか?なぜ注目度が低いのでしょうか。もしかして禁断の世界なのでしょうか。
自転車チェーンの伝達効率について知ることは、禁断の世界に足を踏み入れることを意味するのかも知れません。
実は8年ほど前、米国のとある論文の中に、ギヤーチェーン系の伝達効率の実測結果として、ちょっと驚いてしまうような数値を発見してしまいました。本稿では、その論文をネタに、色々と考えてみたいと思います。マジで禁断の世界かも知れませんよ。
さあ、この先に進みますか?(ていうか、相変わらず前振り長いんだよ!)
Effects of Frictional Loss on Bicycle Chain Drive Efficiency
いきなり横文字ですみません。これは、アメリカ機械工学会の論文誌Journal of Mechanical Designの2001年12月号に掲載された論文です。
筆頭著者は米国ジョンズ・ホプキンス大学 Materials Science and EngineeringのJames B. Spicer教授。シマノの開発者2名も共著者となっています。(残念ながらこの論文はフリーアクセスではありません)
邦題は、
「自転車チェーン駆動系の効率へのフリクション損失の影響」
となりましょうか。フリクション損失というのは、主に、チェーンとギヤの歯が噛み合い、チェーンがギヤ歯に沿うことで「への字」に屈曲することで生じる摺動による損失のことです。上等なチェーン潤滑剤を使えば改善できそうな響きがありますよね。
さて、この論文、実はちょっと看過できない内容となっています。この論文を読んだ私の感想を手短に言うと、
- チェーンの伝達効率が、ある条件下で結構低くて唖然
- これと比べたらペダルとかBBとかハブの軸受ベアリングのフリクション損失なんて%$#💩(-_-;)
です。中身を見てみましょう。
数式モデルは何を語るのか
この論文では、実際のギヤとチェーンを用いた駆動系を作製し、これを用いた周到な実験によって伝達効率を計測した結果を載せています。また、この実験結果を説明するために、極めて論理的な手順で、チェーン-ギヤの駆動系の損失を表現する数式モデルを構築しています。
まず、数式モデルを見てみます。
論文に記載されているやや簡易的な数式 ”式(9)” を引用します。
左辺のPftotalが、フリクション損失(単位はワット[W])です。右辺は、N1がチェーンホイールの歯数、N2がスプロケの歯数、ω1はチェーンホイールの回転角速度で、単位は[rad/s]です。なお、[rad]という単位は、1回転360度を2×π[rad]とする角度表示方式です。
次にµ1は駆動テンション側チェーンとギヤ歯面の摩擦係数(論文の式ではμⅠとなっていますが、誤植です)、ρはチェーンのリンクピンの半径[m]です。T0はチェーンのテンション[Nm]なのですが、実は、リア・ディレイラのテンションスプリングによって発生するチェーンのテンションであり、T0はパンパンに張っている駆動テンションTではないことにご注意ください。
というわけで、注目すべきは、この、チェーンーギヤ系のフリクション損失を表す”式(9)”の中にチェーンテンションの項が、フリーテンション側、つまりリア・ディレイラでもたらされる緩いテンションT0しか入っていないということです。
これはどういうことかというと、ギヤの歯数が決まっていれば、どんな走り方をしたとしても、損失は駆動力の源泉である大きなチェーンテンションの影響を受けない、ということです。
例えば、ケイデンスを維持しながら登り勾配に入ると、トルクが大きくなり、したがって投入パワーが増加するにもかかわらず、損失は増加しない。すなわち、効率がよくなる、ということです。にわかには信じがたいほど単純な話ですが、もう一度、別の言い方をすると、
- チェーンーギヤ系のフリクション損失は、駆動側チェーンテンションに依存しない (式(9)では)
- したがって、効率は、駆動側チェーンテンションの増大(つまり駆動パワー増大)とともに向上する
です。
実は、損失とテンションの関係は論文の中盤、式(15)付近にかなり周到で詳細な記述が載っているのですが、このレビューでは、わかりやすくするために、簡易式ともいえる上記の式(9)に、トルク依存の損失項を新たに設定して、実験結果に合わせこんでみました。どの程度一致するのか、のちほど確認してみます。
実験結果は何を語るのか
さて、実測結果はTable1,2,3などにまとめられていますが、核心部分はTable2とTable3です。以下に論文から引用します。各Tableで着目すべき条件は、次の通りです。
- Table2は、クランク軸入力を100[W]に固定して、ケイデンスとスプロケ歯数を変えています。
- Table3は、ケイデンスを60[rpm]に固定してクランク軸入力とスプロケ歯数を変えています。
いずれの実験においても、クランク軸入力は、わかっています。クランク軸入力の単位は[W]です。
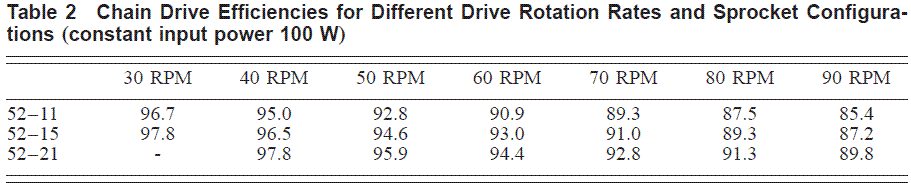
クランク軸に100Wを投入した場合の、ケイデンスと伝達効率の関係の実測結果(James B. Spicer他 “Effects of Frictional Loss on Bicycle Chain Drive Efficiency” から引用)
このTable2は語ります。例えば1行目はギヤ比が固定で52×11、パワーも固定で100Wの場合ですが、
ギヤレシオ固定で同じパワーで走るのなら、ケイデンスは低ければ低いほど、伝達効率が高いですよ~
と言っています。
ははー、なるほど。低ケイデンスで走った方が効率が高いんだ!
いやまあ、そうなんですが、もう少し深読みしてみましょう。
100W走行ですよ。つまり一般的な日本人男子体格かつ伝統的なタイプのロードによる走行であれば平地無風で25km/h前後のサイクリング速度となります。
これを52-11の歯数で走るとケイデンスは42rpm程度。かなり低ケイデンスで全然いい気分じゃないような気がしますが、まあ、分かります。
しかし、Table2の右端は90rpmじゃないですか。つまり、あれ?53km/hほども出ている。たった100Wのパワーでこの車速に到達するためには、6%程度の下り勾配を走らないといけない。
で、同じ100W走行なのにケイデンスは上がるのですから、クランク軸にかかるトルクがずいぶん小さくなる、ということです。そしてこの際、Table2に示される効率が85.4%と低くなっている。すなわち、
「クランク軸投入トルクが小さいほど効率が悪い」
と読むことができます。じゃ、Table2の左端の30rpmは何かといえば、こちらは1.6%程度の上り勾配となります。この場合は効率が96.7%と高い。すなわち、同じ100W走行でケイデンスが下がるので、クランク軸にかかるトルクが大きくなる。というわけで、
「クランク軸投入トルクが大きいと効率が良い」
ということになります。力自慢が有利、みたいな話になりそうですが、ホントですかね?
もう一度、Table2を眺めてみます。少し手を加えさせていただいた次の表。
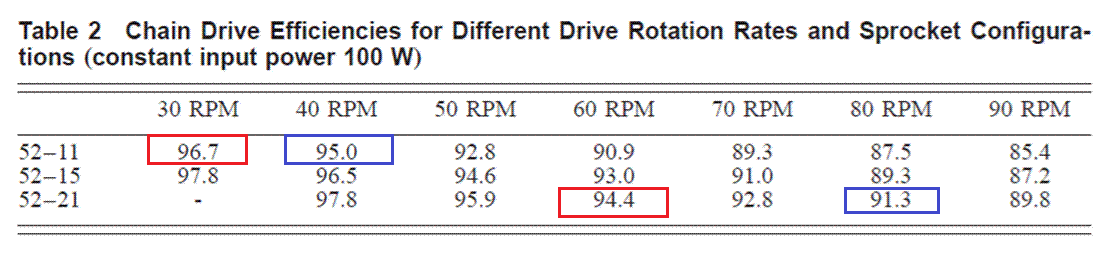
クランク軸に100Wを投入した場合の、ケイデンスと伝達効率の関係の実測結果 (James B. Spicer他 “Effects of Frictional Loss on Bicycle Chain Drive Efficiency” から引用し加筆)
例えばギヤ52-11の30rpm走行と、52-21の57.3rpm走行は同じ速度になりますが、それぞれの効率はどうなっているでしょうか。
Table2によれば30prm走行は96.7%、57.3rpmに近い60rpm走行では94.4%です。表の赤枠の数値です。つまり、30rpm走行の方が57.3rpm走行より2%程度、効率が高くなりそうだということがわかります。
つぎに、ギヤ52-11の40rpm走行は、52-21の76.4rpm走行は同じ速度になりますが、同様に青枠の40rpmと、76.4rpm に近い80rpmを比較すると、95.0%と91.3%ですから、40rpm走行の方が76.4rpm走行より3.5%ほど効率がよさそうだ、ということがわかります。
同じパワーで走る場合はケイデンスを下げれば下げるほど、効率が高くなりそうですね。つまり、再び、
「クランク軸投入トルクが大きいと効率が良い」
ということになりました。
次はTable3です。
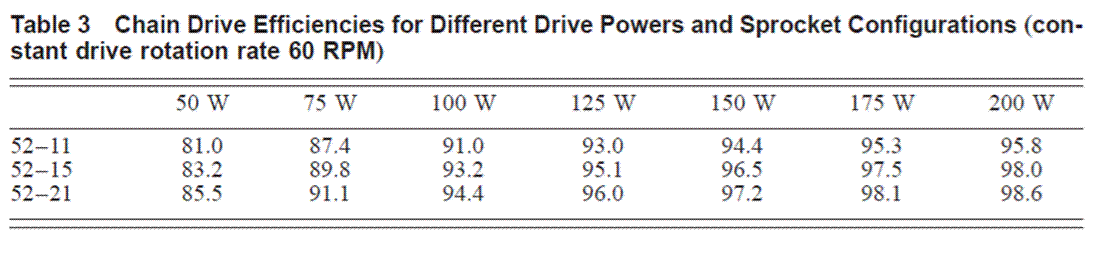
ケイデンスを60rpmに固定した場合の、クランク軸投入パワーと伝達効率の関係の実測結果 (James B. Spicer他 “Effects of Frictional Loss on Bicycle Chain Drive Efficiency” から引用)
例えば1行目。52-11のギヤでケイデンスを60rpmに固定しています。つまり車速が35.8km/h程度で固定。そして走行パワーを50Wから200Wまで上げていくと、効率は81.0%から95.8%まで変化しています。この結果は先ほどのTable1の理解から、何となく腑に落ちます。
ちなみに、50W走行は2.8%程度の下り勾配、200W走行は0.6%程度の下り勾配です。
しかし、3行目の50W列。
あれれ、ギヤが52-21つまり軽いほうの効率が85.5%で、重い52-11よりも4.5%もよくなっているじゃないか?スゲー混乱するんだけど
一見、そんな風に見えますが、52-11と52-21で、ケイデンスが同じ60rpmで走行パワーも同じ50Wなので、クランク軸トルクは同じです。つまりギヤが軽く見えますが、脚にかかる負荷は同じで、軽くなっていない。
一方で、52-21の走行速度は52-11の半分近い低速となり、18.7km/h程度です。ちなみに52-11走行は下り勾配2.8%程度、52-21走行はほぼ平坦路走行です。
つまりTable3は、
「同じケイデンスとトルクで走る場合は、低速ほど効率が良い」
と理解することができます。
簡易な数式モデルで実測値を表現する
禁断の世界は苦しみの世界(笑)。まず、ここまで読んでくださった方に敬意を表します!!
さて、ここから先は論文を引用して新たに行った論考です。
先ほどの式(9)を再掲します。
これはチェーンとギヤの駆動系フリクション損失Pftotal(以降、面倒なのでPfと書きます)を表す式であり、単位は[W]です。クランク軸入力[W]をPcとおき、これとフリクション損失Pfを使うと、駆動力伝達効率ηは、次に示す式(a)のように書くことができます。
また、論文の式(9)で定数と考えてよい部分(リア変速機テンションスプリングに起因するチェーンのテンションT0は定数ではありませんが、ここでは定数と仮定します) をまとめてαと置くことで、式(9)を次に示す式(b)のように書いてみます。
すると、効率の式(a)は式(c)のようになります。
次に、クランク軸トルクTcの効率への依存性を追加します。指数係数βを使って式(d)のように追加してみます。なお、トルクTcですが、クランク軸入力Pc[W]とケイデンスNc[rpm]を用いて、 Tc = Pc/Nc*60/2/π で計算することができます。
式(d)の中で、値がわからないのは、αとβです。
そこで、このαとβを適当な値に設定して、(d)の効率値を実測値の効率になるべく近づけてみよう、ということをやってみます。
Table2とTable3のそれぞれの実測値と、これらに対応して式(d)で得られる数値がなるべく近くなるようにαとβを操作します。
具体的には、Table2とTable3の実測値41個について、実測値と式(c)で得られた数値の差分を2乗し、すべてを合計し、その合計値が最小になるようにαとβを設定します。
このようにして得られたαは0.54、βは-0.29でした。というわけで、論文の式(9)を少々改変した式(d)を実測値でフィッティングした式として、式(e)を得ます。
式(e)でω1はクランクの角速度ですが、なじみ深いケイデンスNc[rpm]を使うと、最終的に式(f)を得ます。
簡易な数式モデルの実力を確認する
論文には結構複雑な数式モデルが載っていますが、一方で先ほど私が式(9)から発展的にでっち上げた簡易数式モデルがさきほどの”式(f)”。これの実力を確認しておきましょう。
まず、実測値であるTable2とTable3をもう一度確認します。表ではわかりにくいので、それぞれをグラフ化してみます(赤丸が実測値)。ついでに、先ほどフィッティングした簡易数式モデルの式(f)を使った結果も同じグラフに載せてみます(青*が式(f)の数値)。
なお、横軸はTable2のグラフがケイデンス[rpm]、Table3のグラフがクランク軸入力[W]、縦軸は効率です。

James B. Spicer他 “Effects of Frictional Loss on Bicycle Chain Drive Efficiency” のTable2の数値をグラフ化(赤丸)し、併せて簡易式(f)の計算結果(青*)を載せた
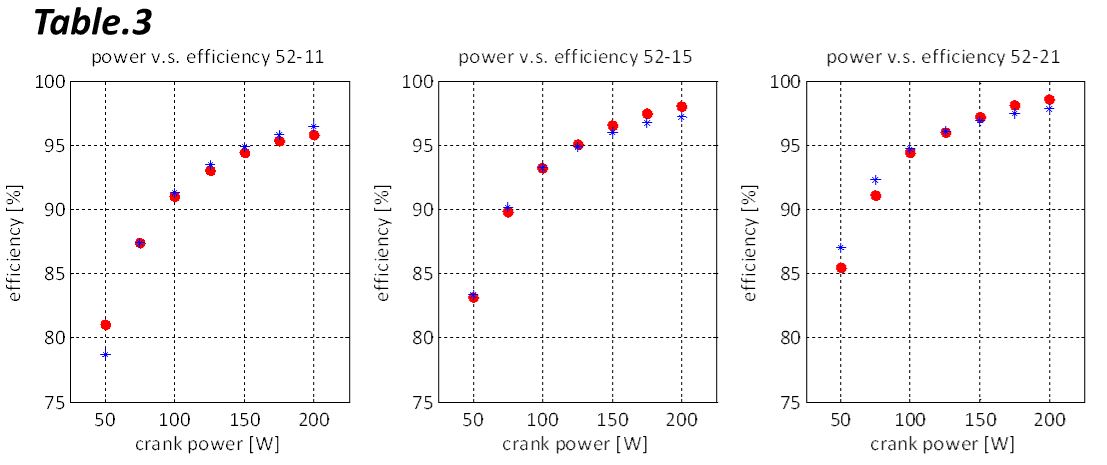
James B. Spicer他 “Effects of Frictional Loss on Bicycle Chain Drive Efficiency” のTable3の数値をグラフ化(赤丸)し、併せて簡易式(f)の計算結果(青*)を載せた
素朴な式(f)ですが、実測値の傾向をそれなりにトレースしており、この式(f)は、ある程度は使えそうであるということがわかります。それにしても、伝達効率がここまでドラスティックに変化するものだとは。何だか迫るものを感じてしまいます(笑)。グラフ化するって偉大ですねぇ。
実験を受けた議論で著者は、
変速機を含むのチェーン駆動系の効率試験は、チェーンリングからリアスプロケットへの動力伝達の全体的な効率が、動作条件に応じて80.9%から98.6%の範囲であることを示しています。
なんて、論文の中でサラッと言ってます。
事例研究
最初にTable2,3の表の数値を眺めたときに、何だかよくわからんなあ、と思ったわけですが、グラフを眺めても、いまひとつ、様子が掴めない、という方もいらっしゃるかと思います。実際、この論文はカンタンそうでいて、意味を正確に理解するのが意外と面倒で、勘違いを容易に誘発するような構造になっています。
結局、どうなるのか?この際ですから作成した式(f)を使って、わかりやすい事例を2つ挙げることで理解を助けたいと思います。
式(f)の適用事例1
【質問】 100Wのクランク軸パワーで平地無風走行している時に、53×21(レシオ2.52)で走った場合と、38×15(レシオ2.53)で走った場合と、53×11(レシオ4.82)で走った場合、効率はどうなるか?
【計算結果】 53×21(レシオ2.52)・・・効率 92.5% (23Cタイヤ時ケイデンス77.9rpm、車速24.73km/h)
【計算結果】 38×15(レシオ2.53)・・・効率 92.5% (23Cタイヤ時ケイデンス77.6rpm、車速24.73km/h)
【計算結果】 53×11(レシオ4.82)・・・効率 94.6% (23Cタイヤ時ケイデンス41.2rpm、車速24.95km/h)
100Wは快調なサイクリングの負荷程度でしょうか。この場合はなるほど、同じようなギヤレシオであれば、効率は同じようなもの、ということですね。53×21つまりアウターで走っても、38×15つまりインナーで走っても、効率は大差なし。また、53×11つまり重いギヤで走ると効率が2%ほどよくなるようです。
式(f)の適用事例2
【質問】 500[W]のクランク軸パワーで平地無風走行している時に、53×19(レシオ2.79)で走った場合と、38×14(レシオ2.71)で走った場合と、53×11(レシオ4.82)で走った場合、効率はどうなるか?
【計算結果】 53×19(レシオ2.79)・・・効率 98.0% (23Cタイヤ時ケイデンス132.5rpm、車速46.49km/h)
【計算結果】 38×14(レシオ2.71)・・・効率 97.9% (23Cタイヤ時ケイデンス136.2rpm、車速46.48km/h)
【計算結果】 53×11(レシオ4.82)・・・効率 98.5% (23Cタイヤ時ケイデンス76.9rpm、車速46.57km/h)
500Wはエリートクラスの巡航パワーです。モダンなTTロードなら50km/h以上で走れるパワーです。この場合はレシオの軽重は効率に大きな影響を与えず、ハイパワーであるというだけでひたすら効率が良い、ということがわかります。
まとめ
以上、禁断の世界(笑)をまとめると次のようになります。
- 同じようなギヤレシオであれば、アウターギヤでもインナーギヤでも効率は同じようなもの
- 高くないパワーでの走行では、レシオを大きく(重いギヤ比)すると効率が良くなる
- 高パワー走行すると効率が良くなる
つまり、誤解を恐れず一言でいえば、
軽いギヤでタラタラ走るとずいぶんと効率が悪いが、とにかくハイパワーな走りで、かつ重いギヤを使えば効率が良くなるゼ!
となります。これがまとめです!
素朴な感想
いずれにしても、この論文は、結局、個人TTで強いような凄い選手ほど好都合になる話を述べていることになります。
100Wでサイクリングする時と、500WでTTを走ってしまう世界レベルの選手の場合とでは、伝達効率が5%程度も違う。
ついでに言うと、シビアな競技シーンでは空力に優れたホイールを履いてTTを走ります。こういった空力パーツをサイクリング走行で使ったところで、空力効果などたかが知れていますが、高速走行であればあるほど、空力アドバンテージが明瞭になります。
つまり、ギヤ効率も空力も、強い選手であればあるほど都合よく作用してくれる、というわけです。凡脚サイクリング派の私としては、何だかちょっと寂しい気持ちにならなくもない・・・。(実は全然気にしていませんが!)
完全に余談
自転車雑誌には方々から様々な商品が持ち込まれ、広告なのか、ニュートラルな記事なのか判然としないページが目立つ月刊誌が出来上がってしまうわけですが、ことチェーン摺動フリクション損失に関して、正面から取り上げた記事は見たことがありません。
一方で、シマノのような総合的な自転車パーツ開発を行う設計・研究の現場は、全体のバランスを考えれば、ホイールの空力抵抗損失の低減、タイヤの転がり抵抗損失の低減、そして、チェーン摺動フリクション損失の低減が、効率向上に関る最重要課題である、と認識しているはずです。
だからこそ、影響が軽微すぎるデュラのハブ軸受ベアリングなどは、ほどほどの等級のモノで(多分)済ませているのでしょう。
チェーンラインからのチェーン角度偏移量(チェーンオフセット)は効率に影響が少ないから、多段化への対応は、出来る限りやる。でも、チェーン摺動フリクション低減の問題はなかなか思うに任せず・・・という感じではないかと想像します。
色々と手を替え品を替え、様々な技術的能書きを携えて新しい自転車やパーツが次々とリリースされ、それなりに注目を集める自転車業界ですが、本来、見過ごすことが出来ないはずのチェーン摺動フリクションについて正面から取り上げることは、もしかしたら、業界タブーなのかもしれません。
一方で、一般ユーザーの目には滅多に触れることがない論文誌には、そんな事情(があるかどうかわかりませんが)など関係なく、実験事実が淡々と述べられている、というわけです。
それから、著者は、
(前略中略)そして、様々な潤滑を試したが、有意な差はなかった
とも論文中で述べています。これに類するデータはかつて某雑誌でも見かけたことがありますが、このようなあからさまな表現をすることもなく、さりげなく数字が並んでいるだけでスルーしていたと記憶しています。(記憶違いかもしれないけど)
さらに余談
この論文を読んだ2012年当時、確認したい点があったので、著者のJames B. Spicer教授にメールでいくつか質問してみました。余談ではありますが、その返事の中に面白いことが書いてありました。教授曰く、
この論文は2001年に著したが、査読を通過した論文の中には、我々と同じような変速機付自転車の効率を示した論文が見当たらない
のだそうです。Spicer教授の論文はアメリカ機械工学会の当該論文誌の論文査読審査を経て、論文として掲載しうるという判断が下されたのち、論文誌に掲載されていますが、変速機付自転車の効率を実測した論文としては、そういった手順を踏んで掲載されたものが他に見当たらない、と。
他にも実測事例はたくさんあるはずですが、査読を通過した論文という形式では少ないようです。というわけで、実測結果としては、この論文の数値はそれなりに信頼性も高く、参考にしてもよいのではないか、と思いました。まあしかし、著者の回答メールは8年前なので、その後の状況に変化があるかも知れません。
というわけで、この論文に興味を持たれた方は、是非、見ていただけたら、と思います。
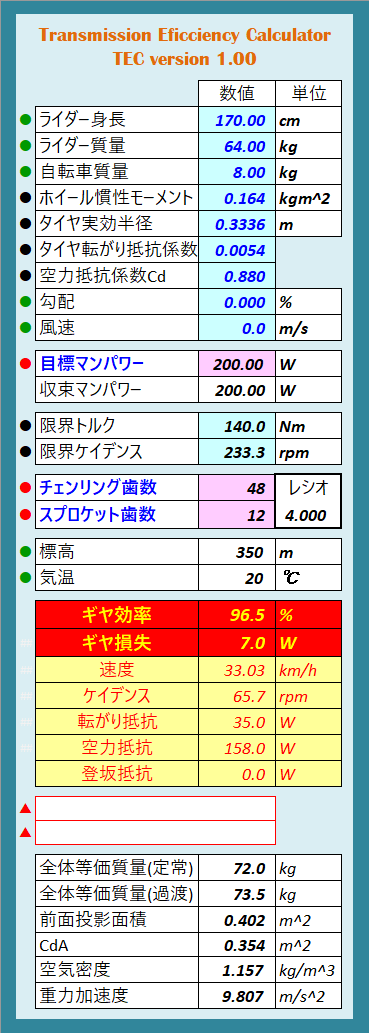
付録 式(f)を実装した禁断(笑)のEXCELシート
前後ギヤ歯数、クランク軸パワーを具体的に与えて、その時のギヤーチェーン駆動系の伝達効率を計算するナンチャッテなEXCELシートを用意しました。ここまで読破して下さった読者限定の企画です!(笑)
次のリンク先からEXCELシートをダウンロードしてご利用ください(スマホEXCELアプリでの利用も可能です)。
ダウンロード TEC (Transmission Eficciency Calculator) version 1.00
TEC version.1.00.xlsxの利用手順
- このEXCELシートを起動します
- 下のようなシートが現れます
- 今回の議論で扱った設定数値は赤丸印をつけた3つの数値です
- この赤丸印の3つの数値を設定します
- 緑丸印の数値は、ユーザに合わせて設定しますが、そのままでも大丈夫です
- 黒丸印の数値には、一般的な数値を入れていますが、適宜変更も可能です
- 丸印が付いている行以外の数値の変更は故障の原因となります
- 以上の数値をもとに計算し、シートの赤セル内に、ギヤーチェーン駆動系の効率を「ギヤ効率」として表示します
数値入力
各行の説明を次の画像の下に続けます。
ライダー身長:身長を入力します
ライダー質量:ウエアやシューズを含めた体重を入力します
自転車質量:自転車の質量を入力します
ホイール慣性モーメント:400グラムリムチューブラホイール+タイヤの標準数値の前後総和を設定しています
タイヤ転がり抵抗係数:良路でのロードタイヤの転がり抵抗係数を想定しています
空力抵抗係数Cd:標準的なマスドロード走行での空力抵抗係数を設定しています
勾配:登坂勾配を%で入力すると、登坂に対応します(下りはマイナス数値)
風速:風速をm/sで入力すると、向かい風時に対応します(追い風はマイナス風速)
目標マンパワー:走行時にクランク軸に投入するマンパワーをWで設定します
収束マンパワー:EXCELに実装したパワー負帰還制御計算の収束値で、目標マンパワーにほぼ一致します
限界トルク:乗り手が発生しうる最大トルクつまり全力スタート時トルクであり、この時の回転数はほぼゼロです
限界ケイデンス:乗り手が発生しうる最高回転数であり、この時のトルク平均値はゼロです(空回り時最高回転数)
チェーンリング歯数:デフォルトとして48を設定していますが、変更可能です
スプロケット歯数:デフォルトとして16を設定していますが、変更可能です
標高:海抜標高をメートルで入力し、高地ほど薄くなる空気密度の影響を空力抵抗に反映させています
気温:気温を℃で入力し、高温ほど薄くなる空気密度の影響を空力抵抗に反映させています
結果表示
ギヤ損失:推定されるギヤ損失W
ギヤ効率:推定されるギヤ効率 %
速度:推定される車速 km/s
ケイデンス:推定されるケイデンス rpm
転がり抵抗:推定されるタイヤ転がり抵抗 W
空力抵抗:推定される空力抵抗 W
登坂抵抗:推定される登坂抵抗 W
▲:不適切な数値を設定するとここにエラーが表示されます
このシートに実装されている計算内容
- 上の結果表示のように、実はギヤ効率以外に、自転車が一定マンパワー走行した場合の各種抵抗値(パワーW)も計算しています
- 単に方程式を解くだけで数値を得ることができるのですが、別用途で作成したEXCEL資源を流用したため、一定パワー走行用フィードバック制御のための計算を実施しており、重いファイルとなっていることをご了承ください(つまり時間軸上で計算しています)