A氏 「オレのゴールスプリント パワーは最大1500ワットだぜ。フフフ」
B氏 「この電気ストーブは800ワット。すげぇ速度出そう」
C氏 「ピラミッド パワー。えっ、単位? 知らね」
非常に柔軟な計測解析機能を備え、発展性もあるPIONEERのペダリングモニターシステムをはじめ、パワーメーターが活況を呈しています。そんな昨今、自転車の世界では何の疑いもなくパワーが何ワットだとかいう会話が交わされますが、パワーって、一体、何なんですかねぇ?
ピラミッド パワーのような難解な概念(?)はひとまず脇に置いて、ここはひとつ、自転車の走行パワーに絞って、わかった気になってみましょう!
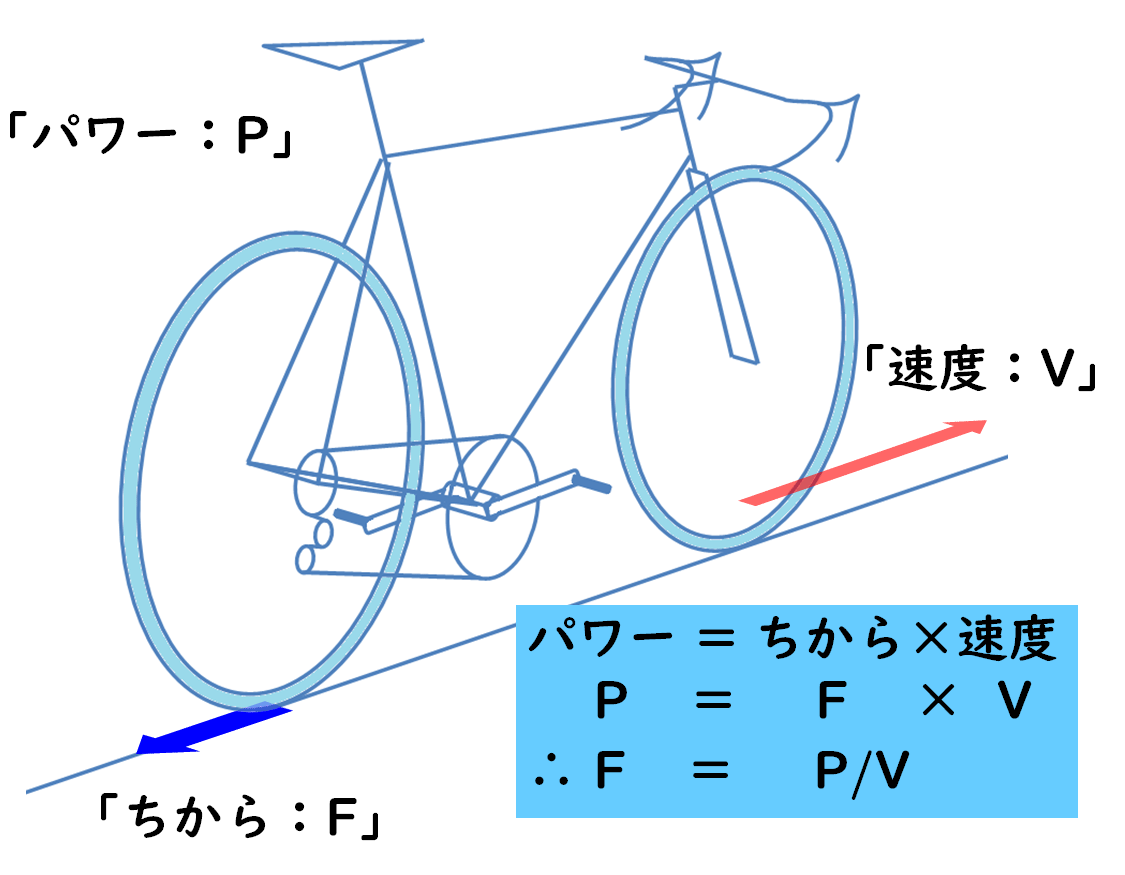
パワーとは、「ちから」と「速度」の掛け算である
いきなりそんなふうに言われても、大体、 「ちから」 ってどこの力なのでしょうかねぇ?
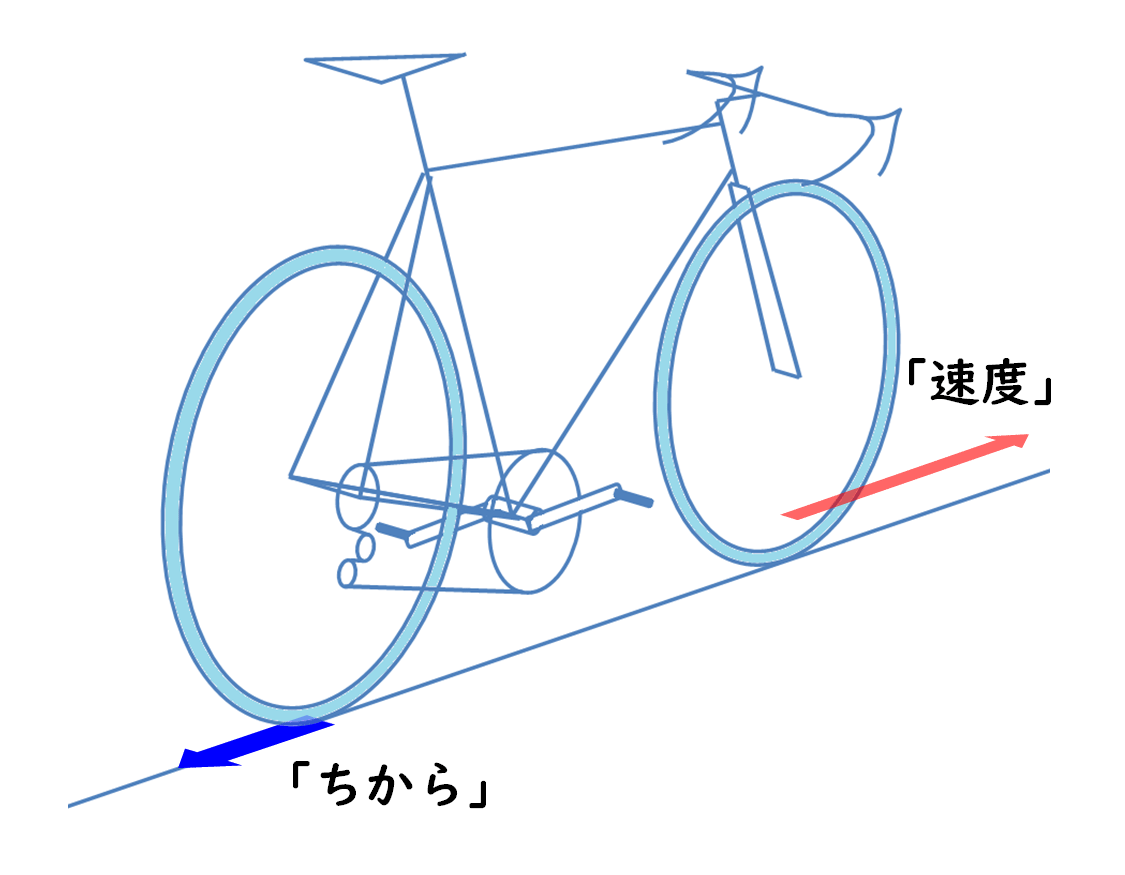
ここで言う 「ちから」 というのは、
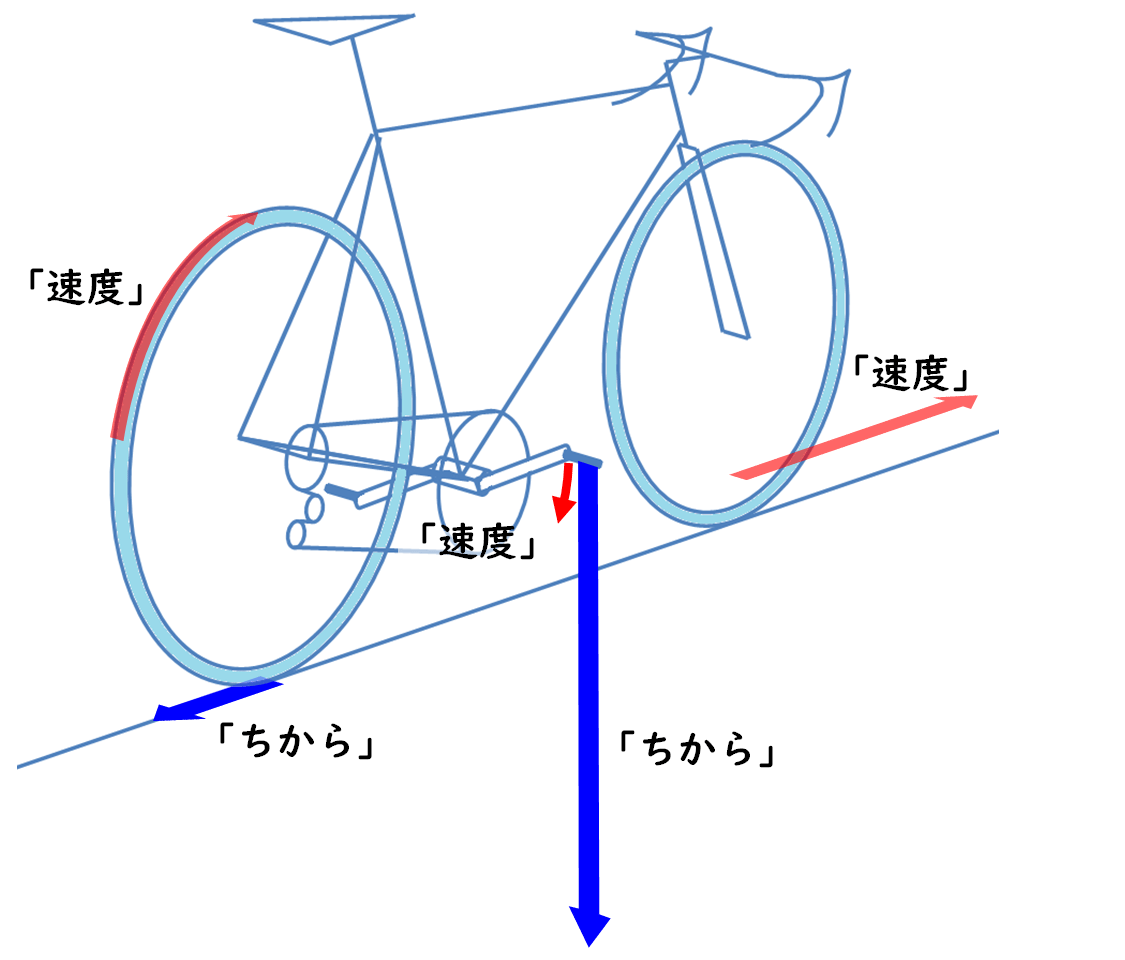
後輪タイヤが地面を後ろに押す「ちから」のこと
自転車が進むのは結局、後輪タイヤが地面を後ろに押すからじゃないですか。だからこそ、次の図の青矢印で示した 「ちから」 には着目せざるを得ないわけです。
そして図の赤矢印が「速度」。
「速度」は、自転車の走行速度そのものである
これは例えば、時速36km/hとかいう、速度。しかし単位が km/h だとちょっと扱いにくいんです。
速度は時速じゃなくて秒速が好都合
どうすればいいか??
時速を3.6で割ると秒速になる
時速の36km/hを3.6で割ってみます。すると、
36 km/h → 10 m/s
というわけで、毎秒10mつまり10m/sという数字になりました。1時間は3600秒なので、1時間あたりの走行距離36000mを3600秒で割ったらそりゃ、10 m/s になるってものです。
で、この時のパワーを250 W、という事にしてみましょう。平地で無風なら大体、そんなもんです。なお、
Wというのはパワーの単位で、「ワット」
すると、
パワーとは、「ちから」と「速度」の掛け算である
ということでしたから、
250W = ちから×速度
これじゃアレなので、250 WをP(つまりPower)、ちからをF(つまりForce)、速度をV(つまりVelocity)として
P = F×V
とします。すると、
F = P/V
パワー250 Wと速度10 m/sを使って、
F = 250/10
というわけで、ちからは
F = 25
「あれれ、単位はどこへ行ったのかな?」
ちょっと説明が面倒なので省略しちゃいましたが、
「ちから」の単位は「ニュートン」で、Nで表す
ので、
F = 25 N
この25という数字を10で割ると2.5ですが、実はこの2.5というのが、青果店などの秤で計った重さ「キログラム」に対応します。2.5キログラムのスイカの重量は、単位Nを使うと、25Nとなる、というわけ。
10で割る、としましたが、正確には9.80665で、これは地球上の重力加速度です。(面倒な話は省略!)
「N(ニュートン)」表示の「ちから」は、9.80655で割って「kgf(キログラム)」表示の「ちから」になる
というわけで
F = 25N = 25/9.80655 kgf = 2.5493 kgf
ところで、この2.5493kgfという数字。ずいぶん小さいと思いませんか?250Wのパワーで時速36kmの走行をしている場合には、タイヤはこの程度の小さいちからで地面を後ろに押しているだけなんですよね。
再びA氏。
「だからさぁ、オレのゴールスプリント時の最大出力は1500ワットだぜ。フフフ」
「それから、オレのスプリントパワーはオレの脚がペダルに力を込めるから生まれるんだぜ。タイヤが後ろに押すって、何だよ?」
「ちから」と「速度」の組み合わせは一通りとは限らない
パワーは、大雑把に分けて2つ、考えておいた方がよいでしょう。
パワー1 → 自転車に投入される乗り手のパワー
パワー2 → タイヤが路面を後方に押すことで発生するパワー
ここまでの話で扱ったのは、「パワー2」の方ですよね。もちろん、自転車のパワーの源は乗り手自身であり、乗り手がクランクを回すからパワーが発生するのですが、そこに着目した場合が、「パワー1」。
この2つのパワーを繋ぐのはギヤやチェンといったトランスミッション系で、パワー1はそのままトランスミッションを経由してパワー2に伝達されますが、
トランスミッションなどの損失(伝達ロス)が無ければ、 パワー1とパワー2は等しい
となります。
パイオニアのパワーメーターなどはクランクで計測するので、「パワー1」を計測していると考えても良いでしょう。また、ハブ軸上で計測するパワータップなどは、「パワー2」に近い、ということが出来ます。もし、タイヤと路面の接触部位で計測することができれば、「パワー2」を計測していることになりますが、製品化は難しいでしょうねぇ。
余談ですが、クランク計測とハブ軸計測。計測精度が十分であるとの前提に立った時、どちらを選ぶべきか?
私は全く何の迷いもなくクランク計測を選びます。しかも左右クランク2ch方式。あっ、いえいえ、両者ともに精度が素晴らしいのなら、両方を同時に使って差分をとって、トランスミッション損失を計測します。(などと言っておきながらそもそも、パワーメーター持ってないし!!!)
さて、
パワー1とパワー2は等しい
ということだったとしても、
「2つが同じだっていうのは、なんとなくわかるけど、この2つはどういう関係なんだ?」
という風に思いませんか?
ちゃんとつながっているんです。
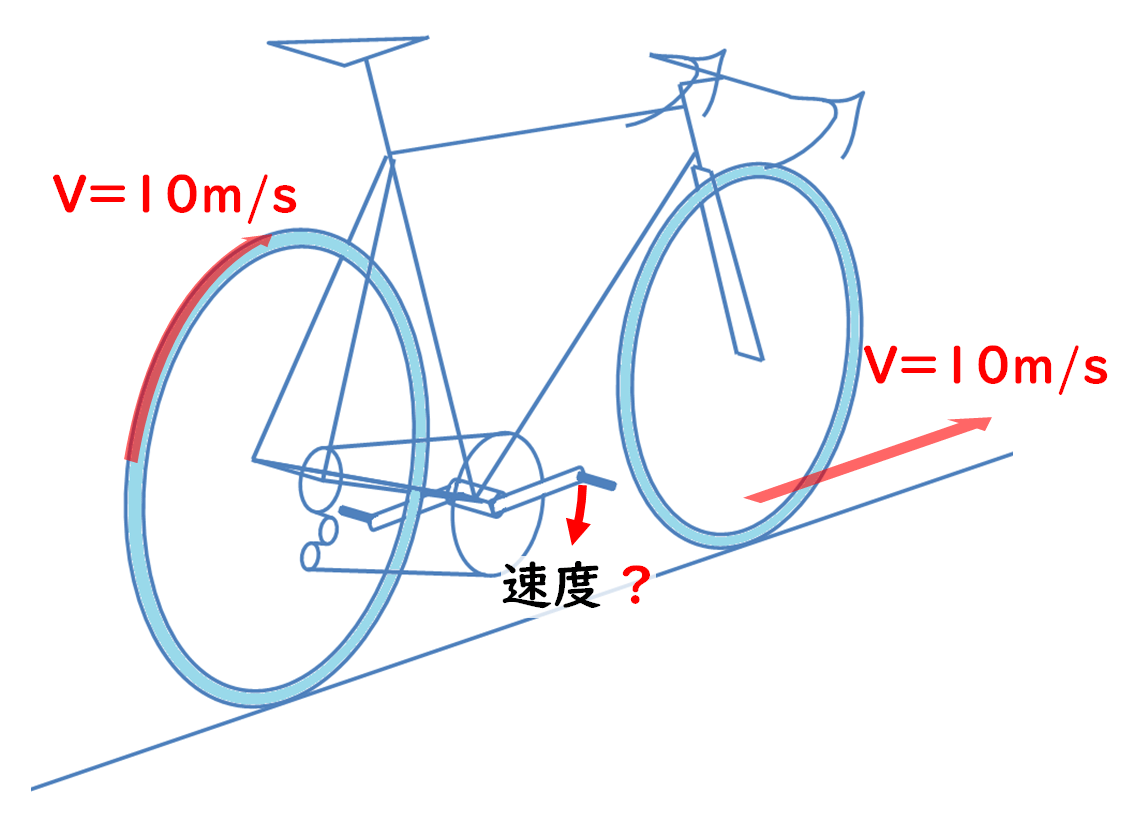
- 700Cタイヤの周長を2.096 mとしてみます。このときのホイール半径は、周長を2π(π(パイ)は円周率3.1415・・・)で割って得られ、その値は0.334mです。
- 次に、ギヤレシオを3.0としてみます。するとクランクのケイデンスはホイールのケイデンスの1/3になります。
- さらに、クランク長さを0.17mとします。
・・・以上、数字が出そろいましたが、ここで問題です!
上の図のペダル軸の速度を導くためには、次のように考えればよさそうです。
まず、ギヤ比が3で、クランクはタイヤよりゆっくり回るから、タイヤ周長速度10 m/sを3で割ればよい。
次に、ホイール半径が0.334mでクランク長さが0.17mということでクランクの方が短いが、この分でも、速度が遅くなるはずだから0.17/0.334を掛ければよい。
つまり、
ペダル軸が回る速度は、「車速/ギヤ比×クランク長さ/ホイール半径」である
というわけで、ペダル軸が回る速度は、
10/3×0.17/0.334 = 1.699 m/s
となりました。
さてさて、速度が1.699 m/sで、パワーは元々与えられていた250 Wですから、今度はペダル軸にかかる「ちから」がわかってしまいます。
F = P/V
だったじゃないですか。というわけで、ペダル軸にかかるちからは、
F = 250/1.699 = 147.18 N
あれれ、巨大! タイヤが地面を押す力が25Nでしたから、その5.89倍もあります。
その雰囲気をイメージすると次の図のようになります。
結局、乗り手のちからが入力されるポイントであるペダルで見た場合と、タイヤと地面の接地面で見た場合で何がどうなっているかといえば、
ペダル軸で見ると 速度が小でちからが大、タイヤで見ると、速度が大でちからが小
と、なっているようですね。
トルクはどこへ行った?
「パワーといえば、トルク。そういえばここまでトルクの話が出てこないけど、それは何かヘンじゃないか?」
いえいえ、ご安心ください。ここまでの話では、パワーの計算を、「ちから」と「速度」で行いましたが、「トルク」を使った計算もちゃんとできます。
タイヤで考えてみます。
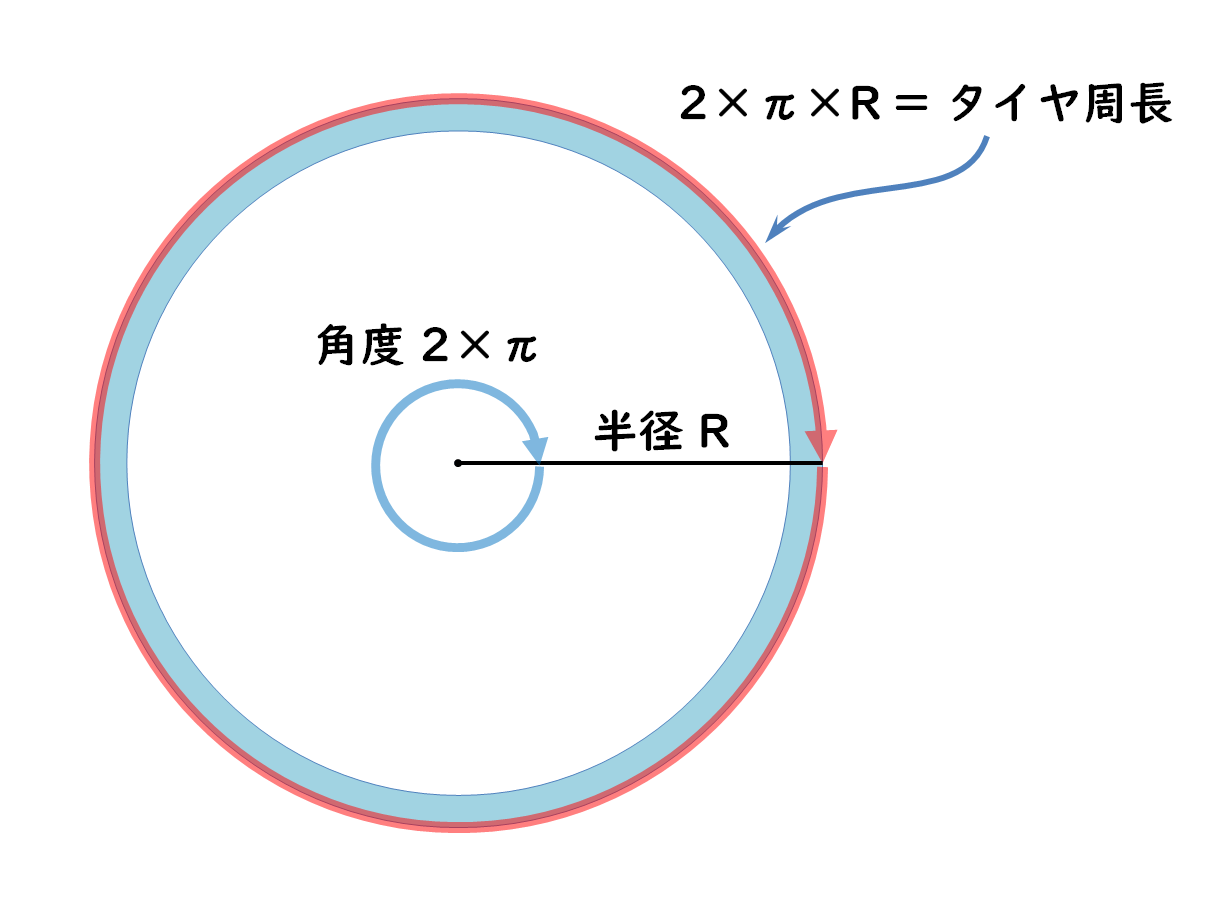
次の図で、タイヤの半径とタイヤの周長の関係は、円周率をπ(パイ)として
2×π×R = タイヤ周長
これは、半径Rを2×πという角度だけぐるりと回すと、円周の長さになりますヨ、という関係を表す式です。πは3.14・・・なので、2×πは6.28・・・ですが、この2×πが実は、360度という角度に等しいという事になります。ただ、2×πの単位は度じゃなくて、ラジアンというヤツなので、6.28・・・ラジアン、という事になります。
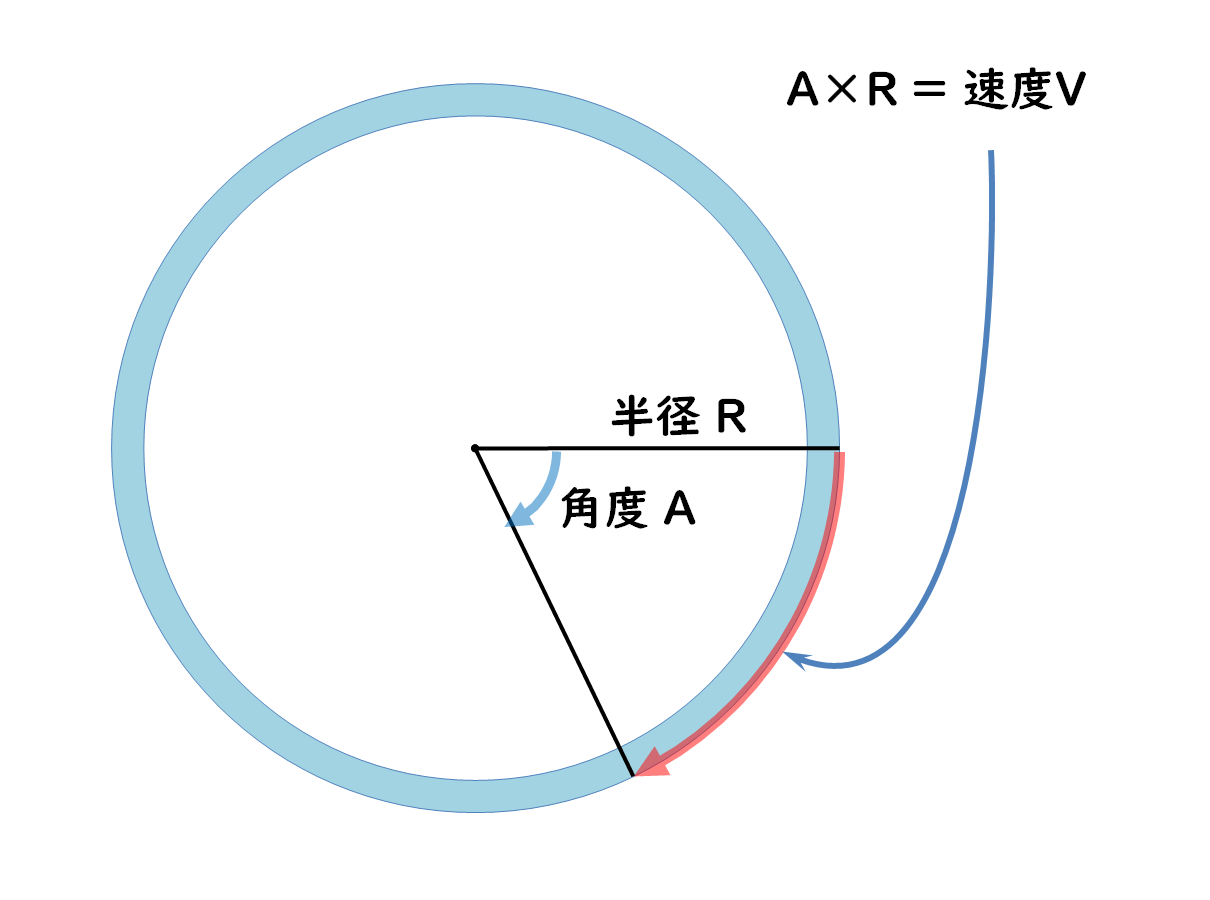
じゃ、次の図のように、角度が2×πじゃなくてAだったらどうか?
2×π×R が タイヤ周長だというのなら、角度がAの場合は、半径の先端は赤矢印のように、長さA×Rの円弧を描くはずです。で、この角度Aが1秒間でホイールが回る角度だとすると、円弧A×Rは、速度Vということになります。
A×R = 速度V
Vは「速度」ですが、一方で、このAのことを、「角速度」と言います。というわけで、
A = V/R
次にトルク(T:Torque)ですが、トルクTというのは、「ちからF」と「半径R」の掛け算で示されます。
ホイール軸のトルクは「ちから」と「半径R」の掛け算である
というわけで、
T = F×R
ちから(単位N)と長さ(単位m)の掛け算なので、単位はNm(ニュートン メートル)となります。
例えばBBの締め付けトルクが50Nmという場合、それはどういう意味かといえば、
1) 1mの長さのレンチの1mポイントのところに、直角に50N(つまり5.1kgf)の力を加える
2) 0.5mの長さのレンチの0.5mポイントのところに、直角に100N(つまり10.2kgf)の力を加える
3) 0.3mの長さのレンチの0.3mポイントのところに、直角に166.67N(つまり17kgf)の力を加える
等々、ということになります。1)2)3)すべてで、「ちから×長さ」が50Nmになっています。
手勘でトルク管理する場合は、トルクの値というよりは、ちからを加えるポイントまでの長さを考慮して得られる「ちから(kgf)」を意識してやると良いでしょう。トルクよりも、ちからのほうがリアルに意識しやすいというものです。そうすれば、レンチの長さが変わったとしても、同じトルクを維持しやすくなります。(完全に脱線)
パワーとは、「トルク」と「角速度」の掛け算でもある
さて、前述のように、トルクTがF×Rとして、また角速度AがV/Rとして与えられましたが、TとAを掛け合わせてみると、
T×A= F×R×V/R
= F×V
おや?「トルク」と「角速度」の掛け算は結局、「ちから」と「速度」の掛け算と同じになってしまいました。つまり、
パワーとは、ちからと速度の掛け算であり、トルクと角速度の掛け算でもある・・・みんな同じだっ! (柳葉敏郎風)
ということになりました。
ペダル軸の「ちから」の向きに要注意
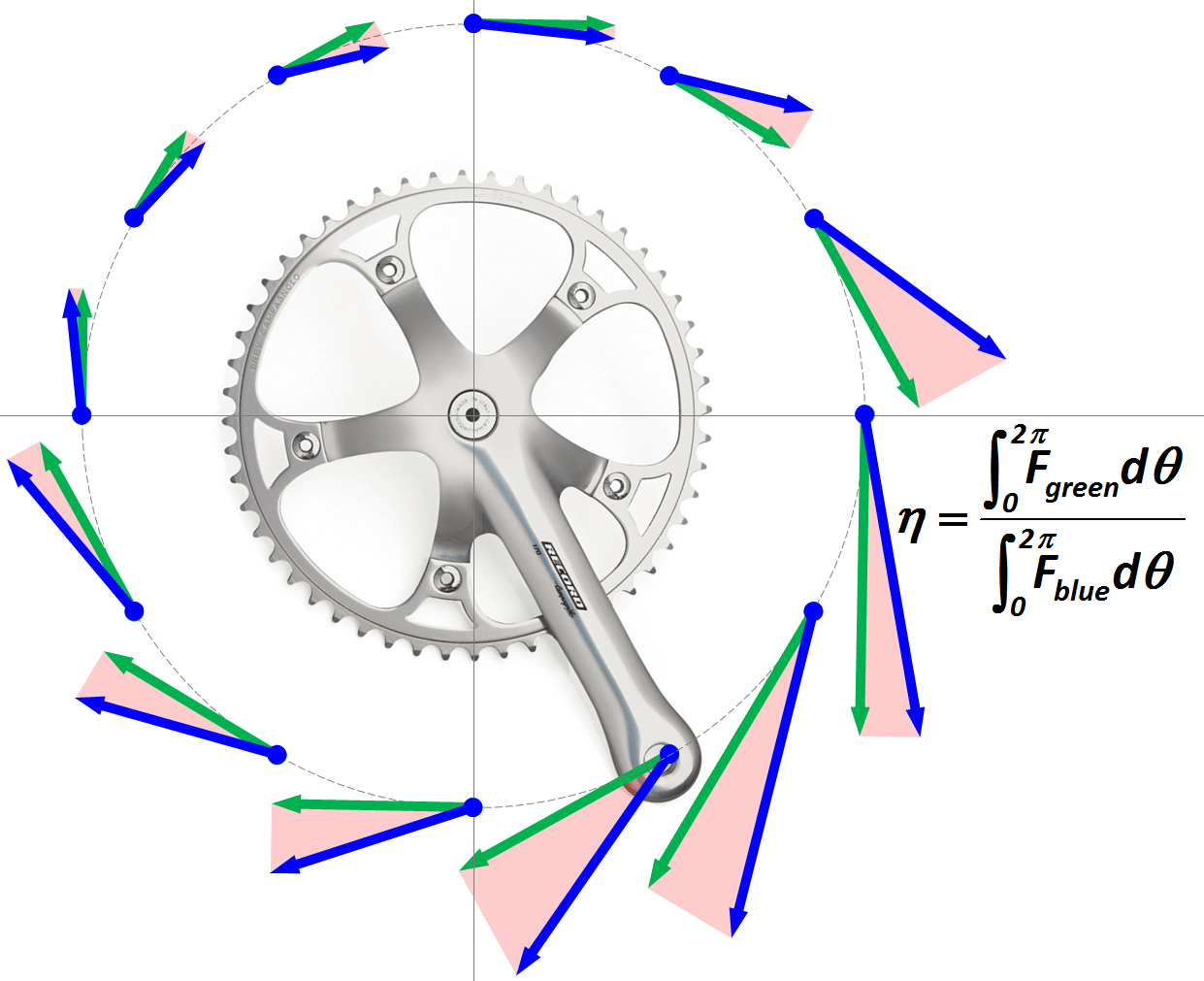
ペダリング効率とは
果たして、ペダルに入る「ちから」が、どこを向いているのか?
気になりますよね。そして、「ちから」の向きがペダル軸の回転の向きからずれている場合、パワー計算のためには、「ちから」を小さく評価しなければならなくなります。巷で言われる「ペダリング効率」と言われている、アレです。
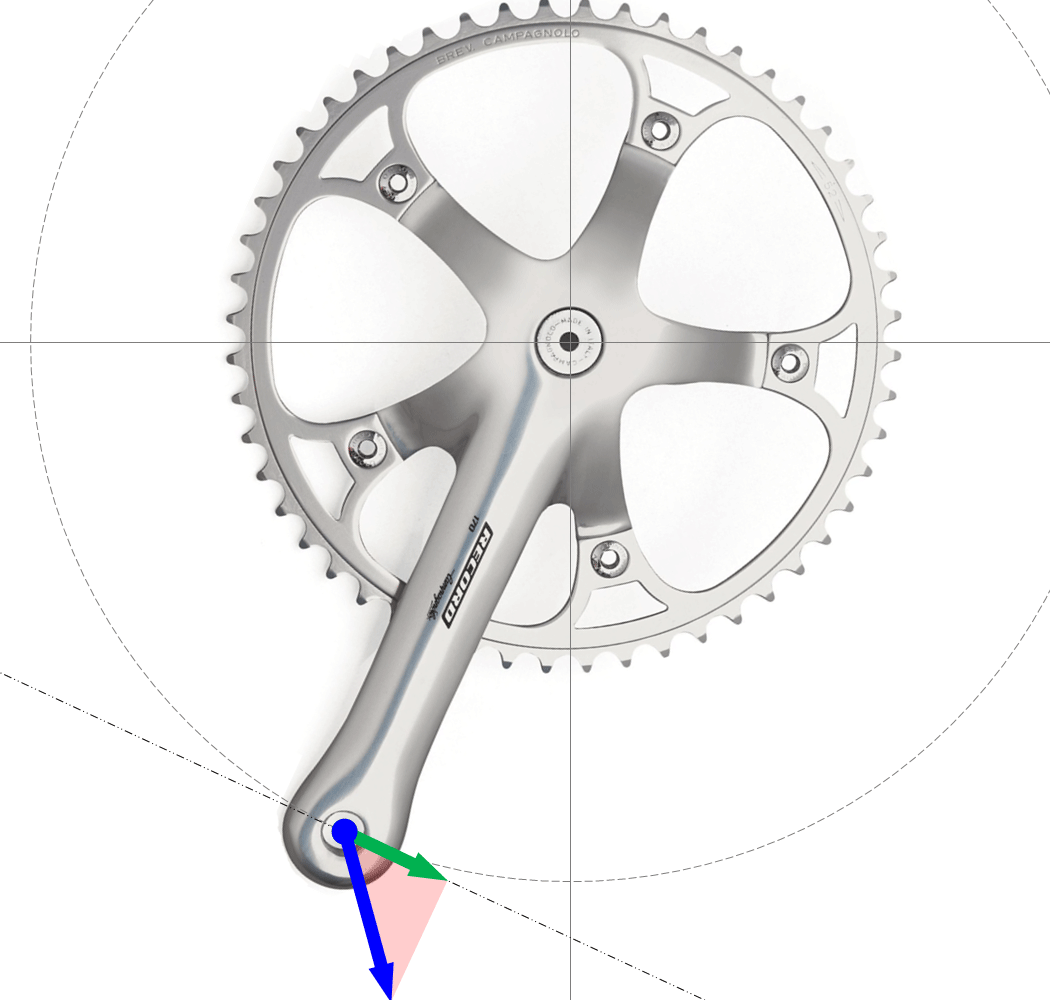
次の図をご覧ください。
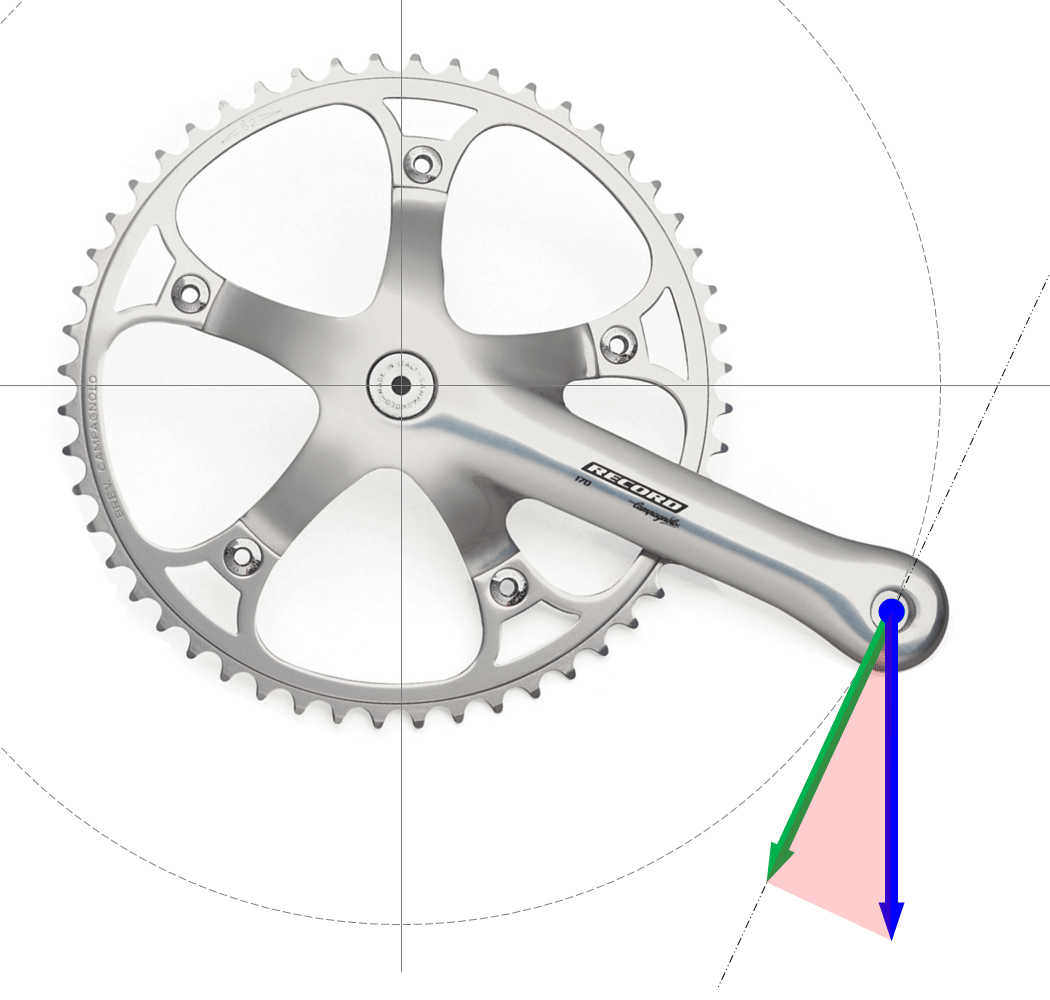
足でペダルを踏んでペダル軸経由でクランクに「ちから」を伝えてるのですが、そのちからの向きが青矢印であるとします。この図ではタマタマ、真下に向かって踏み込んでいます。
で、ペダル軸がグルグルと回って描く円を考えます。ペダル軸ポイントで、この円に接線を引いて、この接線の上に緑の矢印を置きます。次に、踏み込んだちからの青矢印と、接線方向の緑矢印が、図の赤ハッチングのように直角三角形になるように緑矢印の長さを決めます。
こんな風にして引いた緑矢印が、パワー計算に使われる「有効なちから」となります。そして、
緑矢印の長さ/青矢印の長さ
これが、噂の
ペダリング効率
です。
で、注意したいのが次の図の事例。
緑の矢印がクランク回転とは逆方向を向いていますよねぇ。
この場合の緑のちからは、クランクを逆回転させてしまう方向に作用していますので、マイナスのちからということになります。つまり、
緑矢印の長さ/青矢印の長さ < 0
したがって、
ペダリング効率は負の値を取り得る
というわけです。
これは由々しき事態!・・・と思いきや、実は、極めて普通の現象です。例えば、
右足で踏み込んでいるときの左足側
左足で踏み込んでいるときの右足側
というような場面では、よくあることです。引き脚をごく自然に使う人以外は、ほぼすべての人が、コレを発生させていることでしょう。
しかし、ペダリング効率が良ければ楽に速く走ることができるのかと言うと、それはわかりません。
人間の身体は所詮、歩いたり走ったりするという動作をうまく行うようにできています。真円上をグルグル回るペダルに足を固定して下肢と共にリンク機構を形成し、クランクを駆動するなどという、ヒト本来の動作からかけ離れた動作が、「ペダリング効率」という数値に縛られる必要は、無いと思うわけです。
ペダリング効率が良ければ楽に速く走ることができるのか?
というわけで、いくつかの論文を眺めてみました。例えば・・・
“By encouraging riders to maximize the evenness of the crank torque distribution, one encourages an active pull during the upstroke, which decreased gross efficiency in our subjects.”
ライダーにクランクトルク分布の均一性を最大化するように促すことにより、アップストローク中のアクティブプルを奨励したところ、被験者の総効率が低下した。
Effect of Pedaling Technique on Mechanical Effectiveness and Efficiency in Cyclistsから引用
“Most research suggests that when the effectiveness of the force applied on the pedal is optimized, the economy/efficiency (i.e. ratio between mechanical energy produced and physiological energy demand) is reduced (Korff et al. 2007; Mornieux et al. 2008).”
ほとんどの研究は、ペダルに加えられる力の有効性が最適化されると、経済性/効率性(つまり、生成される機械的エネルギーと生理学的エネルギー需要の比率)が低下することを示唆している(Korff ら、2007; Mornieux ら、2008)
Pedal force effectiveness in cycling: A review of constraints and training effectsから引用
・・・いい話がみつかるとは限らないようで。
効率の良いペダリングとは
さて、「効率の良いペダリング」などと、簡単に言いますが、果たしてその定義は何でしょうか。
定義1 効率の良いペダリングとは、「ペダリング効率」の数値が高いペダリングのことである
定義2 効率の良いペダリングとは、同じ速度で走った時に、より疲れにくい走りを実現してくれるペダリングのことである
定義3 効率の良いペダリングとは、同じ速度で走った時に、より気分のいい走りを実現してくれるペダリングのことである
定義は人それぞれで全く構わないのですが、もし、上述の3つの定義が提示されたなら、私は定義3を選択します。次点としては、定義2を選択します。定義1の、ペダリング効率の数値を追求する行為は、定義2に含まれてしまうことでしょう。
また、クランク一回転で平均したペダリング効率に着目した場合には、
同じ「ペダリング効率」を示すペダリング プロフィールは、証明するまでもなく、無数に存在する
のですが、そうなると、その中から、例えば定義2の意味で、最も楽なペダリング プロフィールを決定する作業は、1年や2年では終わらないでしょう。
パイオニアのパワーメーターのお試しで、台上試乗して知ったのですが、私のペダリングは、笑ってしまうくらいに丸いペダリングをしています。まるで踏んでいない!と言っても過言ではないくらいに。30年ほど、思案を重ね続けていろいろやってきたら、知らないうちにこうなっていたという訳なんですが。
速いとか疲れにくいといった評価指標には、一向に興味が湧かない、ただのサイクリストである私は、単に、
「気分がいいぜ!」という評価指標
だけを頼りに自分のペダリングを作ってきました。
ペダリングに正解は存在しない
それにしても想うのは、
自分に合ったペダリングの獲得は永遠の課題である
ということです。「ペダリング効率」を考慮して自分のペダリングを作り上げるのは非常に興味深いことですが、どんなペダリングプロフィールでペダリング効率をどの数値に持っていくのが最良か?という意味で追求しなければ、あまり意味のないものになるでしょう。
ペダリングに正解などそもそも存在しない、または、ペダリングの正解は無数に存在する
したがって、アカデミズムの方々にしてみれば研究ネタが尽きないし、雑誌編集者にしてみれば雑誌ネタもつきない。というわけで研究者は延々、研究を続けることができるし、雑誌は、様々な解釈、立場から毎年、特集記事を企画することができる、ということになります。(いけねぇ、言いすぎちゃったかな?)
完全に脱線!!
まとめ
パワーとは、着目する点における「ちから」と「速度」の掛け算であり、また、「トルク」と「角速度」の掛け算でもある。
OVERLANDER
売り上げランキング: 36,095
▼ GlennGouldさんのその他の自転車考察系記事はこちらから読めます