平坦で快適な道は、交差点を境にして5%の登坂に切り替わった。時速35キロで軽快に飛ばしていたオレのロードバイクの速度がどんどん落ちていく。
「うっ、なぜだ。どうして登坂に入るとこんなにも無常に、速度がどんどん落ちていくんだ?」
気が付けば時速20キロを割り込んでいた。上り坂とは非情なもので、容赦などしてくれない。
「一体誰なんだ、オレを後ろから引っ張るヤツは。出てきやがれ!」
気配を感じて振り向くと、身軽そうな若者が何食わぬ顔でオレに迫っていた…
登坂があるからサイクリングは楽しい
登坂のないサイクリングなんて、由美かおるのいない水戸黄門のようなものだ
これには異論があるかもしれませんが、
坂をのぼるのは、平地を走るよりも大変だ
これは、自転車に乗るほぼすべての人が感じていることだと思います。登坂ではそれなりの力をペダルに与えないと登れませんし、脚をとめたらすぐに止まってしまいます。
それにしても、登坂走行が平地走行よりも肉体的に大変なのは、なぜなのでしょう?
「そんなの、わかりきったことじゃないか!」
まあ、それはそうなんですが、そんな当たり前のことを、少し真面目に考えてみます。
乗り手のパワーのゆくえ
乗り手は、ペダルを通して自転車にパワーを与えています。この、乗り手が自転車に与えたパワーは一体、どこに使われているのでしょうか。
企業では、複式簿記の流儀で貸借対照表(バランスシート)を毎年作成し、財務状況を関係方面に開示しています。これによって財務バランス(会社が所有しているお金や財産、借金などの状態)がわかります。
似たような発想で、自転車のパワーバランスを示す、「パワーバランスシート」とでもいうべきものを作成してみましょう。
まず、ひとつの例を挙げます。
次の1つ目の表が、平地無風の良路で、乗り手が250Wをロード自転車に投入した場合の、マンパワーの行先。
2つ目が、勾配5%で無風の場合で、同じく250Wを投入した場合の、マンパワーの行き先です。乗り手は170cmで体重が66kg、自転車と合わせて74kgの質量を想定しています。それぞれにおける車速は、35.6km/hと、19.1km/hです。
▼平地無風の良路で、乗り手が250Wを出力した場合のパワーバランスシート
| パワーバランスシート@平地/無風 | |||
|---|---|---|---|
| パワー投入の部 | パワー運用の部 | ||
| マンパワー | 250W | ギヤ系駆動抵抗 | 8.4W |
| タイヤ転がり抵抗 | 43.0W | ||
| 空気抵抗 | 198.6W | ||
| 登坂抵抗 | 0.0W | ||
| 合計 | 250W | 合計 | 250W |
| (車速35.6km/h) | |||
▼上り勾配5%で無風の場合で、乗り手が250Wを出力した場合のパワーバランスシート
| パワーバランスシート@勾配5%/無風 | ||||
|---|---|---|---|---|
| パワー投入の部 | パワー運用の部 | |||
| マンパワー | 250W | ギヤ系駆動抵抗 | 3.8W | |
| タイヤ転がり抵抗 | 23.1W | |||
| 空気抵抗 | 30.8W | |||
| 登坂抵抗 | 192.3W | |||
| 合計 | 250W | 合計 | 250W | |
| (車速19.1km/h) | ||||
パワーバランスシートの左側には、パワー投入の部として、マンパワーの250Wだけが計上されます。一方、右側には、パワー運用の部として、4つの抵抗による消費パワーが計上されます。
この4つの抵抗というのは、
- ギヤ系駆動抵抗
- タイヤ転がり抵抗
- 空気抵抗
- 登坂抵抗
です。
抵抗の科目は、細分化しようと思えば、いくらでも細分化できますが、自転車という乗り物のパワーバランスをわかりやすく理解するためには、まず、この4つに着目することが重要でしょう。こういった表は多分、商業高校出身の方とか、会社で会計部門にいるとか、簿記が趣味だ、などという方には、スーッと腑に落ちるのではないかと思います。しかし、
「う~む、表はピンとこないなあ」
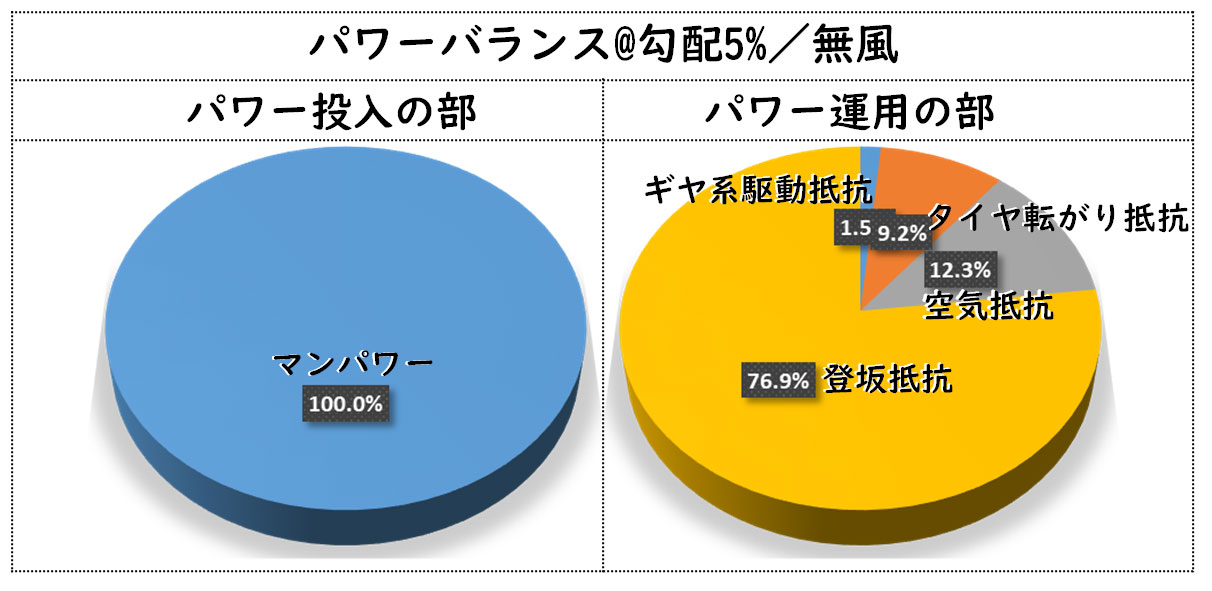
という方も多くいらっしゃると思います。そこで、円グラフを用意しました。
平地と登坂の違い
先ほどの円グラフを見ると、その違いは明白で、
登坂では、平地では無かった登坂抵抗が現れる
これが平地と登坂の違いです。
「あたりまえだろ!」
と言われてしまいそうですよねぇ。
そうなんですが、なんと、乗り手が自転車に与えた100%のパワーのうち、登坂抵抗が76.9%を占めています。激坂にはまだ遠い5%で、このありさまです。なんだかスゴ過ぎませんか?せいぜい5%の登坂なのに、登坂抵抗が平地の主役である空力抵抗に代わって抵抗の盟主に昇格です。
なお、登坂になると表の中のギヤ系駆動抵抗が減るのが、ヘンだな~、というご意見があろうかと思いますが、アメリカ機械工学会の論文誌Journal of Mechanical Designの2001年12月号に掲載された論文のデータを参考に計算した結果です。なぜそうなるかに関しては、次のCBNレビューを参照ください。
参考 [論文] Effects of Frictional Loss on Bicycle Chain Drive Efficiency
登坂抵抗はどこからやってくるのか
いきなりですが、階段の話。階段を駆け上がるときに、
- 1秒で高さ1mだけ上る
ということを考えてみます。
「えっ?2段飛ばしでグイグイ上れば毎秒1mの高度を稼ぐなんて簡単じゃね?」
なーんて想像したりしませんでしたか?
例えば、体重が66kgのAさんの場合、この勢いで駆け上がるには、なんと647.24Wの出力が少なくとも必要なんです。大雑把に言って、あのファビアン・カンチェラーラが大爆発して集団を引き離す場面のパワーに匹敵するかも知れません。(*1)
さて、登坂抵抗はどこからやってくるかといえば、
地球が乗り手を後ろに引っ張っているから
です。
「何言ってんだ。地球がオレのサドルに手をかけているとでも言うのか?」
はい。地球の重力ってやつが、あなたのサドルに手をかけているんです。(いやサドルじゃないけど・・・)
パワーとは 「力×速度」 である
というのは、CBNブログで以前触れたことがありますが、この「力」(蚊じゃなくて、ちから)に相当するのが、地球の重力です。
体重が66kgのAさんが体重計に乗れば、66kgと表示されるんですが、あれは、地球がAさんを地球の中心(重心)方向に引っ張っていて、この地球による力を受け止めた体重計が、その力を測って表示しているわけです。
ここで約束事ですが、重力加速度というヤツがあって、それが9.80665なのですが、コレを体重という質量に掛けると、力になるんです。つまり、
地球が及ぼす力 = 66kg × 9.80665 = 647.2323 N
単位「N」は「ニュートン」と読みますが、これは力の単位です。
この力647.23Nに、階段を駆け上がる速度を掛け算すると、パワーになります。つまり
647.23 N × 1 m/s = 647.23 W (*2)
というわけで、階段で毎秒1mの標高を稼ぐのはものすごい負荷の運動だ、ということがわかります。登山の急登もそうですが、長い階段を本気で駆け上がったら、自転車ヒルクライムのタイムアタックの時と同じような滝汗状態になります。
次は自転車。
今度は、乗り手と自転車の合計が66kgだったとして、これを毎秒1mだけ持ち上げるために必要なパワーは?
やっぱり647.23 W。
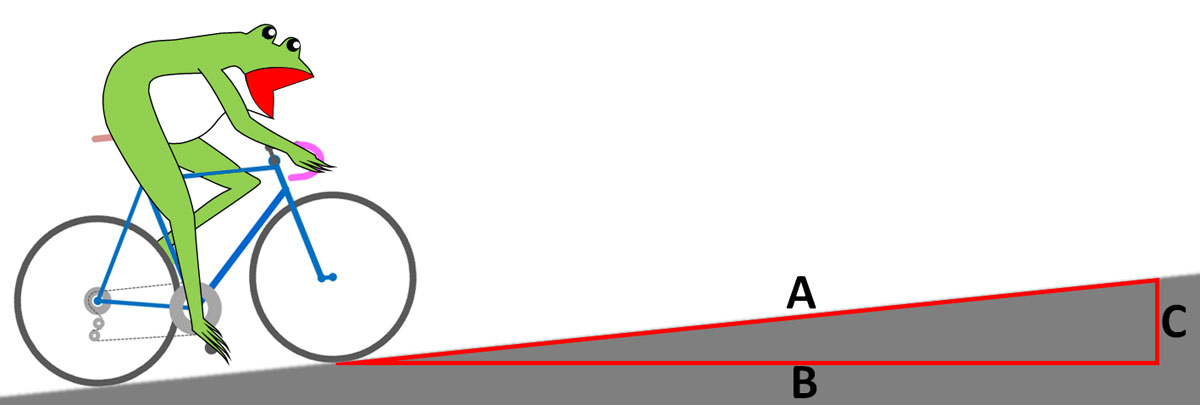
ここで、登坂勾配を定義しておきます。次の図で、三角形ABCを考えます。辺Aは路面に沿っています。つまりタイヤが転がって走行距離となる辺です。辺Bは、水平移動距離に相当します。そして、辺Cが、登坂量となります。登坂勾配は、
登坂勾配 = C/B
で定義されます。C/Aではないんですよね。つまり、10%の勾配と言ったら、それは例えば、Bの長さが10mで、Cの長さが1mであり、C/B=0.1の場合をいいます。この時、Aはいくつかといえば、10.049876・・・mです。つまり、秒速10.049876・・・m/sで走って、1秒間に1mだけ標高を稼ぐ登坂は、10%の勾配、となります。
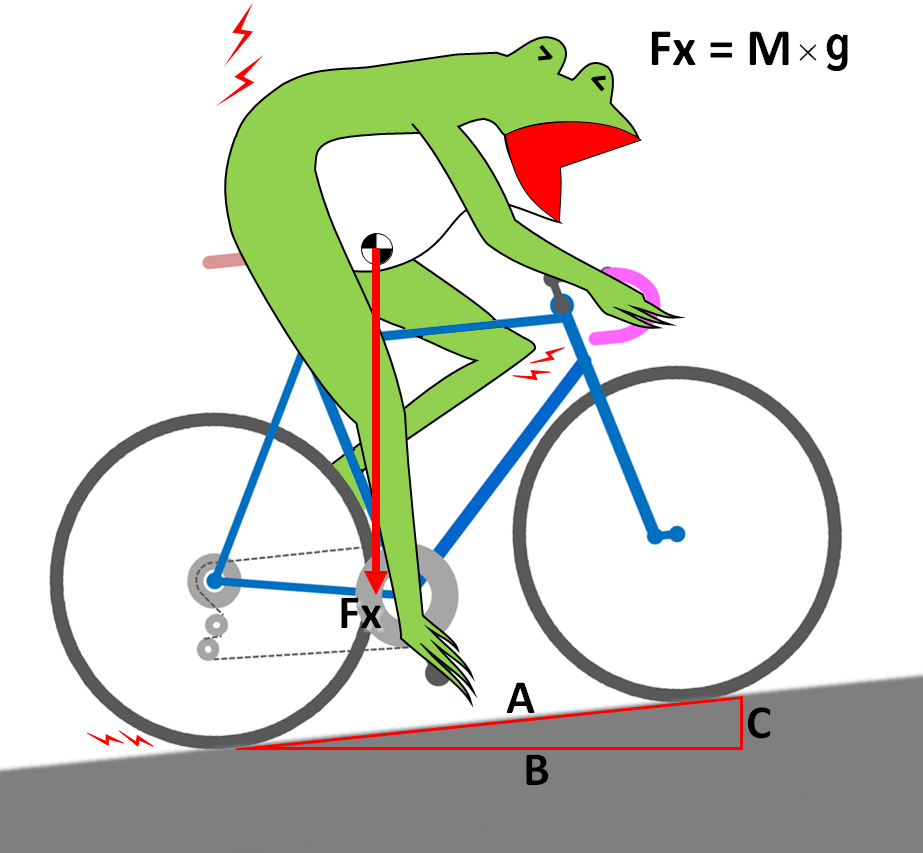
平地と登坂の重力作用
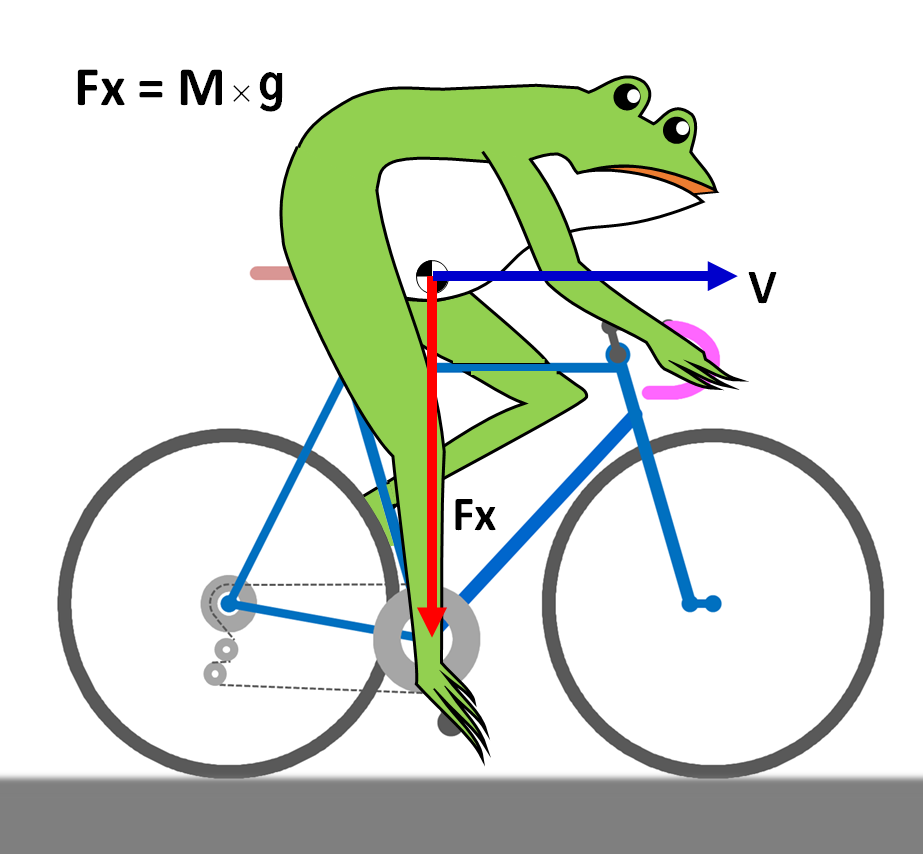
平地走行時に自転車と乗り手にかかる重力を考えます。車速は時速36km/h、つまり秒速10m/sとしておきましょう。
自転車と乗り手を総合した重心に重力がかかりますが、これを、
Fx = M×g
と表しておきます。次の図のように、重力Fxは真下の向きにかかります。Mは自転車8kgと乗り手66kgの全体の質量で、74kgとします。gは重力加速度で、9.80665・・・です。したがって、Fxは、
Fx = M×g = 725.68 N
です。
平坦路を走行していますので、自転車の車速は、この重力の矢印と直角の方向に発生しています。図の赤矢印Fxが力、青矢印Vが速度です。
パワーとは力×速度である
と書きましたが、実は、パワーの発生は、力と速度の矢印の向きが揃っているかどうかに、大きく依存するんです。となると上の図。力と速度が直角で、全くパワー発生に寄与していないということになります。最初に登場したパワーバランスシートの登坂抵抗がゼロ、というのはコレが原因です。
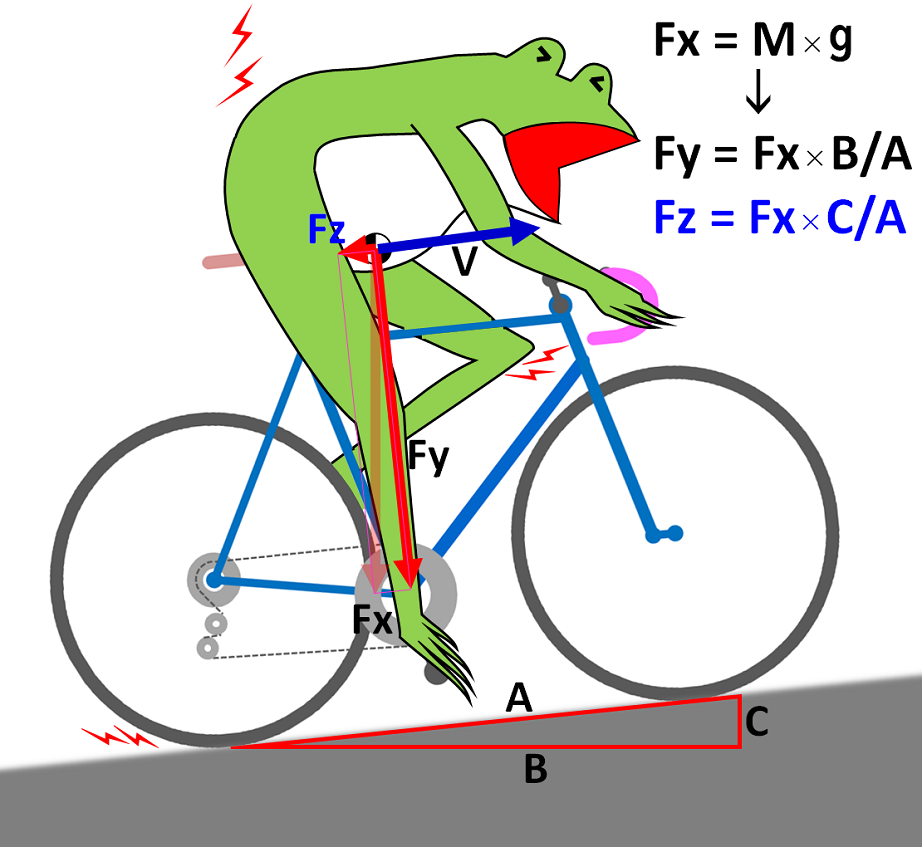
次に、10%登坂走行時。
重力Fxは同じですが、真下に向かって作用するため、道路とは直角になりません。路面側に三辺の長さがA,B,Cの三角形を書いていますが、登坂勾配は、
C/B = 0.1 = 10%
です。
ここで、Fxを路面Aに垂直な成分Fyと、路面Aに直角な成分Fzに分けて考えます。
矢印Fyの先端に、矢印Fzを継ぎ足すと、Fzの先端が、元の矢印Fxの先端と一致するのですが、こんな風にして、Fxを、FyとFzという、2つの力で代用することができます。Fzが路面と平行ですが、もちろん、速度の青矢印Vも路面と平行です。
力の矢印Fyを見てみると、コレは車速Vの向きと直角の関係になっているので、登坂パワーの発生に寄与しません。しかし、短い矢印Fzと車速Vはいずれも路面と平行ですから、2つは同じ方向の関係(向きは逆)になっています。登坂抵抗はこのFzと車速Vの関係で算出することができます。こんなに短い矢印が絶大な影響を及ぼすということです。まず、力Fzは、
Fz = Fx×C/A = 725.68×1/10.049876 = 72.21 N
ここで、既出のように、C=1mの場合には、A=10.049876mです。まあ、10でも構いませんが。(本稿は有効数字の扱いがダメすぎですが、暫しご勘弁を)
次に、Fzに車速10m/sを掛けて、
登坂抵抗 = Fz×10 m/s = 72.21 N×10 m/s = 722.1 W
となります。かなりすごい数値です。図で見ると10%なんて大したことないんじゃないか?と思ってしまいそうですが、全然、そんなことはないんです。平地で移動するだけだと気が付きませんが、
重力に抗うのは大変
という、当たり前すぎることが数字で示されました。
一方で登山の急登。こちらはヘタすりゃ勾配が70%(傾斜角度で35度)なんていう場面もあるわけで、地球の重力に抗う仕事が大半になります。垂直梯子など、そのまんまですね(勾配無限大、つまり傾斜角度90度!!)。垂直梯子といえば、ボルダリング・・・
ボルダリングの登坂パワー
ボルダリングの種目に、「スピード」っていうのがありますよね。15mの垂直壁を、ぼぼ直線的にものすごいスピードで這い上ってタッチ板にタッチするという競技。世界記録は5.48秒だそうな。タッチ板までの距離が地上から15mといいますから、13mほど這い上がってタッチすることになります。5.48秒で13mですから、速度は 13/5.48 = 2.37 m/s。毎秒2.37mです!
仮に、選手の体重が60kgだと仮定すると、身体にかかる重力は
F = 60kg×9.80665 = 588.4 N
というわけでパワーは、力に速度をかけて、な、なんと
P = 588.4 N×2.37 m/s = 1394.5W
体重が70kgならば、1626.9kWです。あの手掛かり足掛かりと、あの態勢で、この出力。これはとんでもない数値じゃないでしょうか。重力に徹底的に抗う超瞬発系の競技ですから、体脂肪率を極限まで落とすことが競技力の向上に直結する、ということが想像されます。すごい競技ですよねぇ。
参考 スピードのルール
下り坂はどうなる?
さて、登坂は大変だというのは分かったとして、じゃ、下りはどうなんだ?
- 下りは楽だけど、誰かが引っ張ってくれているのか?
- 下りは、何もしなくても速度が上昇して、やがて一定の速度になるような気がするけど、それって一体、どうなってるんだ?
- 重い人ほど下りが速いような気がするけど、そういうものなのか?
一体、どうなってるんですかねぇ?
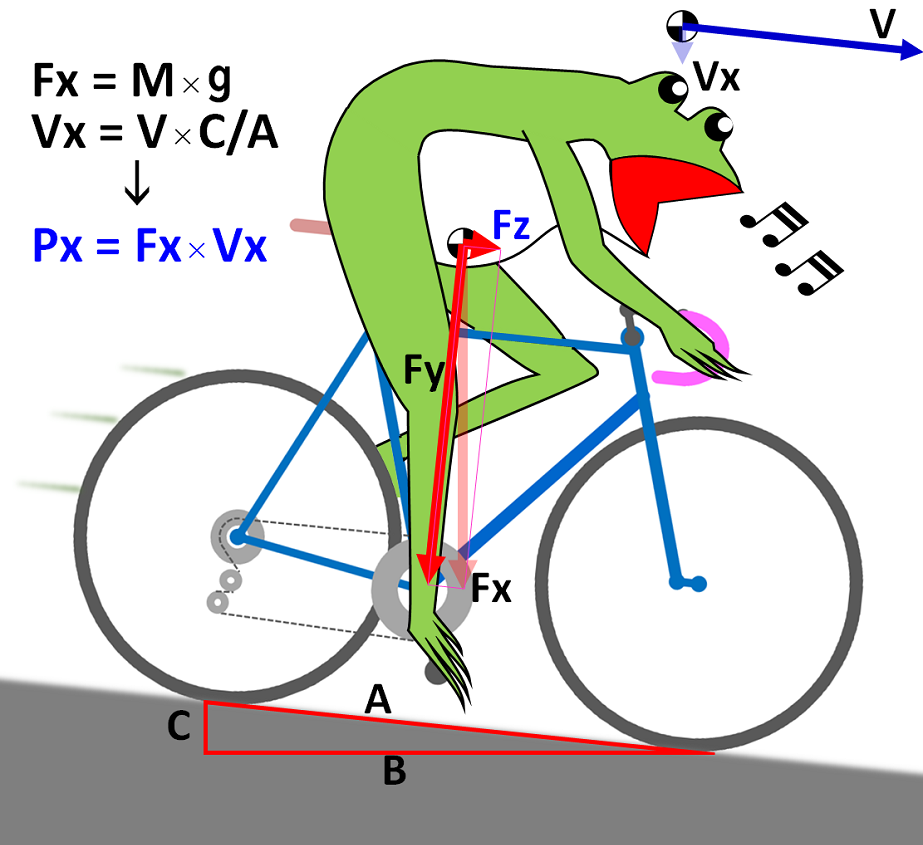
次の図。
ある人が車速Vで5%の下り坂を、ペダルを回して下っているとします。便宜上、右上に移して示した青矢印の車速Vは、例えば時速54km/h、つまり15m/sです。三角形ABCで、C/Bが下り勾配5%、つまり0.05、C/Aは0.0499376…です。
さて、直線下りで仲間と脚を休めて並走(危険なのでクルマがこないところでどうぞ)したときに、なぜか自分のほうがだんだん仲間より前に出てしまう、という経験をお持ちの方、いらっしゃると思います。
「おおーっ、オレの自転車は最高級の回転系で潤滑剤も高級と来ているだけあって、回転がスムーズだぜぃ!」
とかなんとか、雑誌インプレの知識を総動員して高性能パーツの効能を言いたくもなりますし、いや、まあ、その可能性も捨てきれませんが、どちらかというと、あなたの体重が他の仲間より重い、というのが原因であることの可能性のほうが高いでしょう。
なぜこんなことが起こるのか?
それは、
同じ速度で下る場合、重いほうが地球からの仕事をよりたくさん享受することができるから
です。何言ってるんだか、ちょっとよくわかりませんよねぇ。
上の図で、重心にかかる重力Fxは
Fx = M×g
これは真下に向かってかかる力で、平地でも登坂でも同じです。
次に重心の速度Vです。路面に平行なVに対して、これの真下に向かう成分Vxも薄い青矢印で図に示しました。
Vx = V×C/A
です。ここで注目!力Fxと速度Vxは、平行になっています。しかも、登坂の時と違って、力Fxと速度Vxが同じ向きを向いています。そして、
パワーとは力×速度である
ということを適用すれば、落下方向のパワーは、
Px = Fx×Vx = M×g×V×C/A
体重+車重が74kgとして、数値を当てはめると、
Px = 74kg×9.80665×15m/s×0.0499376 = 543.6W
というわけで、
下りでもらえるパワー = 543.6W
「ええーっ、下りで543.6Wも地球からもらっているのか!?」
そぉーなんです。偉大なる地球アシスト!
このパワーを地球からいただいた上に、さらに乗り手のパワーを加えて、5%の下り坂を時速54km/hで下る、というわけです。ところで、5%の下りを時速54km/hで走るために必要なマンパワーは、
必要なマンパワー = 226.1W
これに地球からもらうパワーが543.6Wですから合計は、769.7Wです。というわけで、この769.7Wというのが平地を時速54km/hで走るときに必要なマンパワーとなります。(と言いたいところですが、下りと平地ではギヤへの負荷が違いすぎるのでギヤの伝達効率がかなり違ってきて、769.7Wより小さくなりますが・・・)
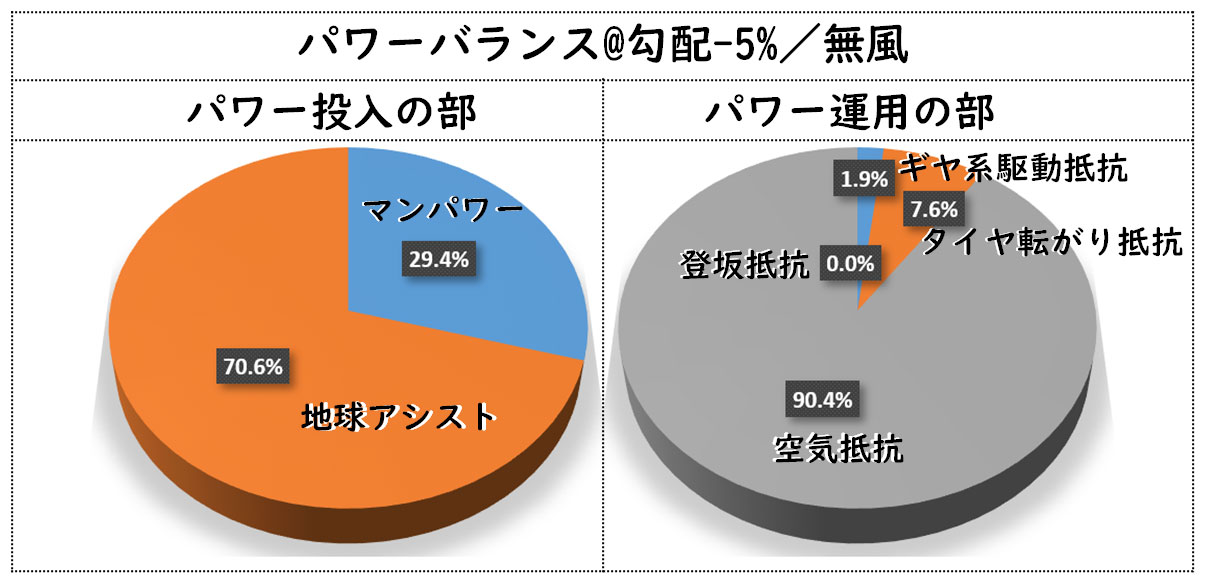
5%下り勾配54km/h走行時のパワーバランスシートは次の通り。
▼下り勾配5%で無風の場合で、乗り手が250Wを出力した場合のパワーバランスシート
| パワーバランスシート@勾配-5%/無風 | |||
|---|---|---|---|
| パワー投入の部 | パワー運用の部 | ||
| マンパワー | 226.1W | ギヤ系駆動抵抗 | 14.9W |
| 地球アシスト | 543.6W | タイヤ転がり抵抗 | 58.7W |
| 空気抵抗 | 696.1W | ||
| 登坂抵抗 | 0.0W | ||
| 合計 | 769.7W | 合計 | 769.7W |
| (車速52km/h) | |||
惰性走行の最終速度
次に考えるのが、5%下り勾配での惰性走行最終速度。
5%の下り勾配で極低速から惰性走行を開始した場合、最初は加速しますが、やがて、ある一定の速度に落ち着くことでしょう。その速度は如何ほどか?
速度Vで下った場合の地球アシストパワーは、
Px = Fx×Vx = M×g×V×C/A
でした。この式の右辺には質量Mが掛け算の形で入っています。つまり、アシスト量が体重に比例するということです。重い人の方がたくさん地球からアシストされる。ということは、惰性走行最終速度も、重い人の方が大きくなるだろう、と推測されます。
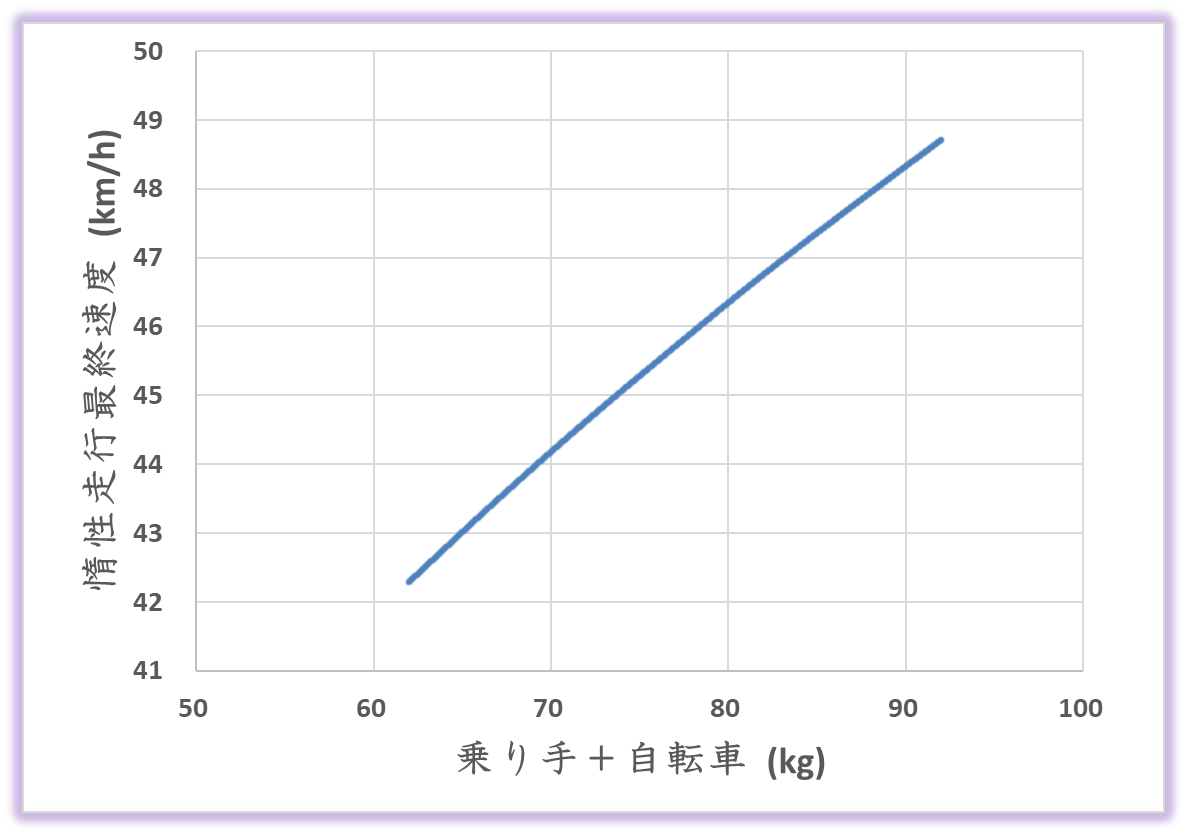
計算結果です。身長が170cmの乗り手の体重が5kg増加すると、惰性最終速度がおよそ1.1km/hだけ増加します。(※体重増による前面投影面積の増大にともなう空力抵抗増大、転がり抵抗増大分も含んだ結果です)
さて、速度Vで下った場合の地球アシストパワーを再掲すると、
Px = Fx×Vx = M×g×V×C/A
ですから、地球アシストパワーPxは速度Vにも比例します。つまり、
降坂速度に比例して、地球アシストパワーは大きくなる
ということです。
一方、空力抵抗のパワーですが、こちらは速度の3乗に比例してどんどん大きくなります。下り道でゆっくり下り始めて、その後、惰性で速度が増大すると、地球アシストパワーが速度に比例して増大するので、最初のうちは加速しますが、やがて、空力抵抗が速度の3乗でグワーッと立ち上がってきて、地球アシストパワーに迫ってきます。
この空力抵抗と転がり抵抗の和が地球アシストパワーと拮抗したところで、惰性降坂の最終速度になります。
次のグラフは、170cm、56kgの乗り手と76kgの乗り手が、8kgの自転車で速度ゼロから惰性降坂したときの速度の時間変化を示しています。最終的には時速4km/h以上の速度差となります。
というわけで、2つのグラフから、惰性降坂では重い人がだんだん前に出てしまう、ということがわかります。
まとめ
- 登坂は、地球の重力に抗う仕事である
- 5%の上り勾配を250Wの出力で登坂した場合、一般的な男子の体格の乗り手であれば、その3/4程度が登坂パワーに配賦される
- 降坂では地球の重力場が乗り手を強力にアシストする
- この地球アシストパワーは車速と質量に比例する
まあ、何がどうであれ、登坂は、楽しい!ということで、おあとがよろしいようで。
(*1) 例えば個人TTでの出力がどの程度になるかに関しては、次の2019年ツールでの個人TT解析が、登坂や降坂も含めて詳細に分析しており、なかなか興味深いですよ!
参考 Tour de France 2019: Individual Time Trial Analysis
(*2) 「あれぇ、階段を駆け上がるのは確かに1秒で1mだけ上がるけど、垂直に走るわけじゃないから、速度は1m/sよりも速いはずだゼ??」
ですよねぇ。階段の勾配が30度(角度で30度の勾配というのは、58%の勾配と同じです。超々激坂!)だとすれば、垂直に1m/sで駆け上がる場合には、同時に、水平方向の速度が約1.73m/sとなり、階段に沿った速度は2 m/sになります。
というわけで、駆け上がる人は、実は同時に水平移動のためのパワーも発生する必要があるんですが、水平方向はゆっくりしたジョギング程度の速度なので大したパワーではなかろう、ということで今回は無視しています。
しかし、時速40km/hの世界に達する陸上男子100mの国際大会決勝での水平方向の出力は、多分、1000Wを優に超えているでしょうが、その計測方法も含めて、興味深いですねぇ。
▼ GlennGouldさんによるその他の自転車考察系記事はこちらから読めます