・・・次のニュースです。twitterの500名投票で、1000回のパンクのうちリアのパンク回数が717回であることが判明しました・・・
「ほんまかいな？」
朝のMHKニュースに疑念がよぎった。
「お、おれは76回もパンクしてリアのパンク確率80%を導き出したんだぞ。それはcbnblogで既報のとおりだ。
76回もパンクしているんだから信頼性も十分のはず。ところが500名投票の結果が717回ってことは、71.7%じゃないか。低くないか？」
「オレは昨日や今日、パンクし始めたわけじゃねーんだよ！！」
宅浪は心の中で吠えた。
パンク経験についてお聞きします。
直近の過去2回のパンクで、フロントとリアのどちらがパンクしましたか？— CBN (@cbnanashi) May 20, 2020
cbnblog「パンク頻度の実学的考察」のなかで、世の中の自転車好きと思われる母集団から得られた500名の標本集団による全1000件のパンクのうち、717件がリアのパンクである、という結果が得られたことを報告しました。実に1000件もの事例が集められたわけで、この結果の統計的な有意性はかなりのものです。
この数字をそのまま引用して、
リアタイヤがパンクする確率は71.7%付近と思われる
と言っても間違いとは言えないでしょう。
これに対して、
「ええーっ、オレなんか最近、フロントが4回連続してパンクしてるけど、そんなことあるのか？」
という方も、世の中にはおられるはず。リアタイヤがパンクする 「確率」 が仮に、71.7%であるとすると、フロントがパンクする確率は28.3%となります。したがって、フロントが4回連続でパンクする確率は、
0.283の4乗 = 0.0064 → 0.6%
となります。これはかなりレアな事態なわけで、「オレは呪われている！」 と言いたくなるレベルですが、しかし、無いわけではないということは、言えます。
500名の投票で得られたリアのパンク率71.7%という数値。これをそのまま「確率」と読み替えて、その数値71.7%という 「確率」 が真値であると仮定しましょう。この確率71.7%のもとで、たとえば、
ある人が走り続けて1000回パンクした場合、リアは一体、何回パンクするのか？
これをチラ見してみます。
「リアがパンクする確率が71.7%」 とは？
たとえば、これまでに1回のパンクを経験していて、それがリアタイヤだった場合は、
リア1回／パンク回数1回 = リアタイヤのパンク100%
です。2回のパンクを経験していて、それが前後1回ずつだった場合は、
リア1回／パンク回数2回 = リアタイヤのパンク50%
というわけで、1000回のパンクを経験していて、リアタイヤが717回だった場合は、
リア717回／パンク回数1000回 = リアタイヤのパンク71.7%
ということになります。パンク確率が71.7%と言ってしまってもよさそうなものですが、実は、確率が71.7%かどうかは、この時点ではわからないので、ここでは確率という言葉を使っていません。
硬貨のような均整の取れた円盤物体は、何十万回も投げると、表の出る率が限りなく50%に近づくでしょう。その場合は 表の出る確率が50% などと言います。
もし、パンクという事象が、何十万回ものパンクの末にやがてリアタイヤがパンクする率が71.7%に限りなく近づくようなものであるならば、
リアタイヤがパンクする確率は71.7%である
と言っても良いでしょう。これは、
次にリアタイヤがパンクする確率は71.7%である
ということも意味しています。次のパンクのことを言っていますので、それまでリアが連続5回パンクしたから、次は、フロントじゃね？という「予感」などは介入する余地がありません。
ひとりが100回パンクする場合
リアタイヤがパンクする確率は71.7%である
をまずは受け入れてみましょう。この場合、ひとりの自転車乗りが走って、100回のパンクを経験した場合、前後タイヤがどんな順序でパンクして、やがてリアタイヤのパンク率が71.7%に近づいていくのでしょうか。
これを机上で実験するために、乱数を使います。1回の試行で0以上1以下の範囲で全ての実数、つまり0.22436…とか0.80119…とか、が同じ確率で一様に現れるタイプの乱数です。
この乱数を生成し、数値が0.717以下だった場合にはリアのパンク、0.717より大きい場合はフロントのパンク、ということにします。
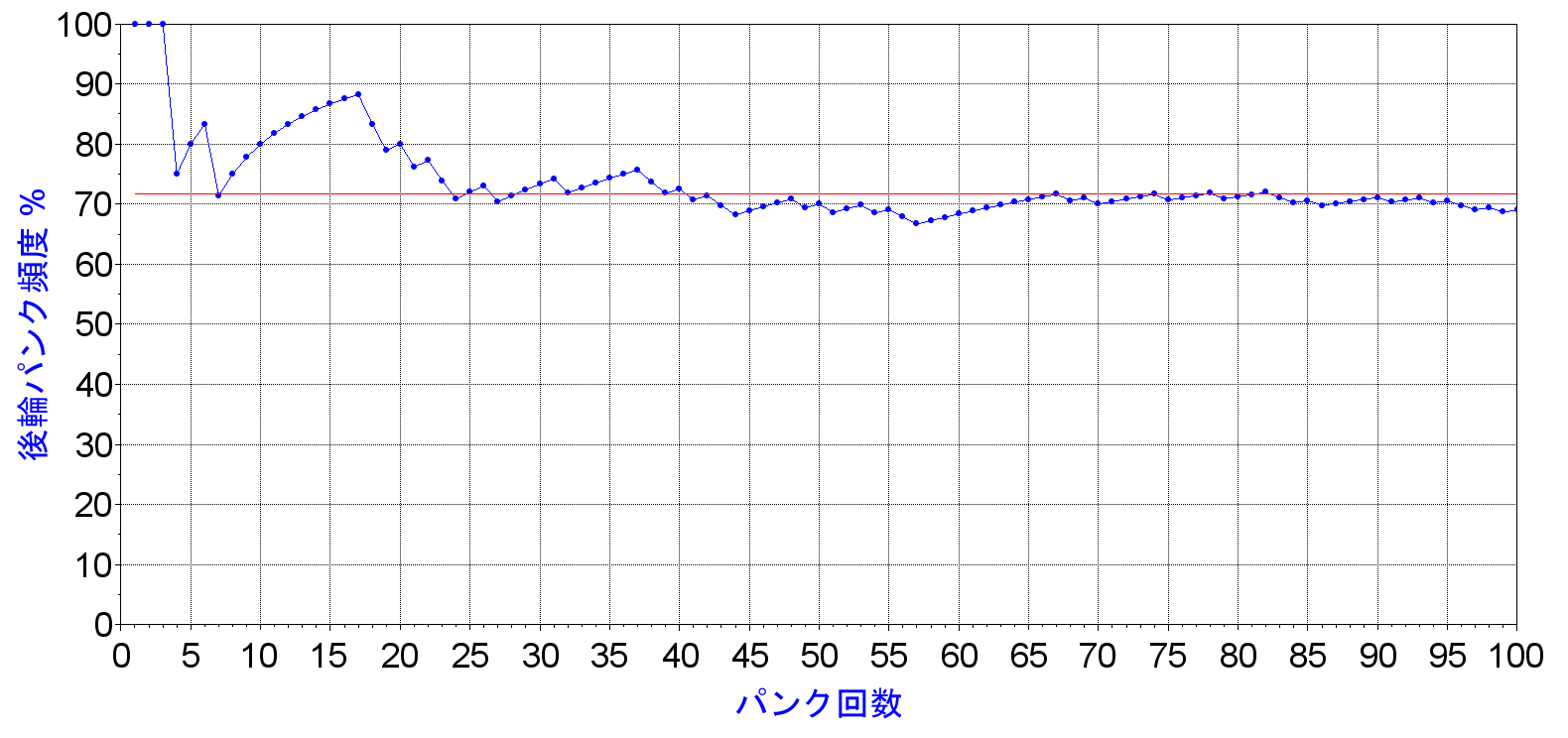
というわけで、乱数を100回発生させて得た結果です。
ひとりが100回パンクした場合のリアタイヤのパンク頻度推移
横軸が、パンク回数、縦軸がその回数までの段階でのリアタイヤのパンク頻度(パンク率)です。赤線が71.7%ライン。
このグラフ事例では、最初の3回が100%に貼りついています。これは、3回連続してリアがパンクしている、ということを意味します。そして4回目のリアタイヤパンク頻度が75%となっています。これは4回目にフロントがパンクしたため、4回のうち3回がリアタイヤのパンクということになりますので、75%というわけです。
こんな風にしてパンク回数を増やしていくと、パーセントが増えたり減ったりしながら、71.7%の赤線に少しずつ近づいていきます。8回目から17回目まで、10回連続リアがパンク！という場合も存在します。
「またリアがパンクかよ！」
ですが、リアが10回連続してパンクする確率は、
0.717の10乗 = 0.036 → 3.6%
最初に示したフロントが4回連続する場合が0.6%でしたから、それに比べるとありそうな事象ではあります。
ところで、このグラフには折れ線が1本しかありません。つまり、ひとりの人が100回パンクした、という、たった1回の事例に過ぎないわけです。当然、乱数を発生させて計算しているだけなので、この計算をやるたびに、上のグラフの折れ線は違う経路をたどります。つまり人によって履歴はさまざま、というわけです。
では、ひとりではなく、100人かそれぞれ100回パンクしたら、100本の折れ線がどんなふうに描かれるのでしょうか？
100人がそれぞれ100回パンクする場合
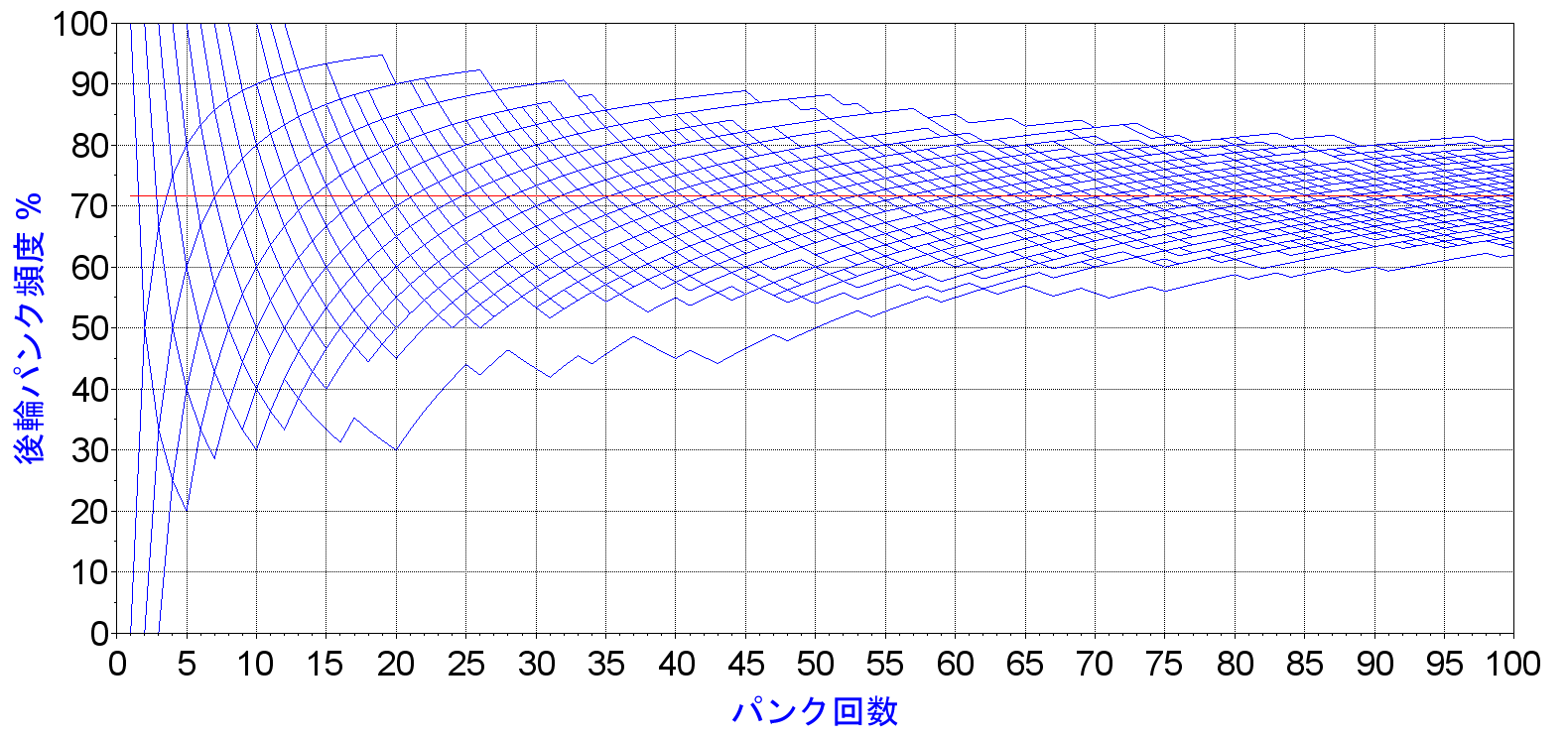
所詮、確率で規定した机上計算でしかなく、いずれ71.7%の赤線に近づくとはいえ、100人が100回パンクしたらどうなるんですかねぇ？次がその結果です。目がチラチラするのでドットは省略して線だけの表示にしています。
100人がそれぞれ100回パンクした場合のリアタイヤのパンク頻度推移
全体としては徐々に収束していく傾向であるとはいえ、バラつきがすごいですね。100回目のパンクのところを見てみると、大体62%から82%まで、約20%の幅があります。100回もパンクしたのに、です。つまり、もし私が実際に100回のリアルなパンクデータを持っていたとすると、
「リアタイヤのパンク頻度は60~80%程度である」
という表現にとどめておいた方が、どうやらよさそうである、ということが言えるかと思います。また、10回程度のパンクでは、リアのパンク頻度が高いとハッキリ言うのはちょっと難しいかな、という気がします。
では、このグラフのパンク100回目で、100人はそれぞれ、リアタイヤのパンク頻度がどこに落ち着いているのか？その分布を確認してみます。それが次のグラフ。
100人がそれぞれ100回パンクした時点でのリアタイヤのパンク頻度の分布
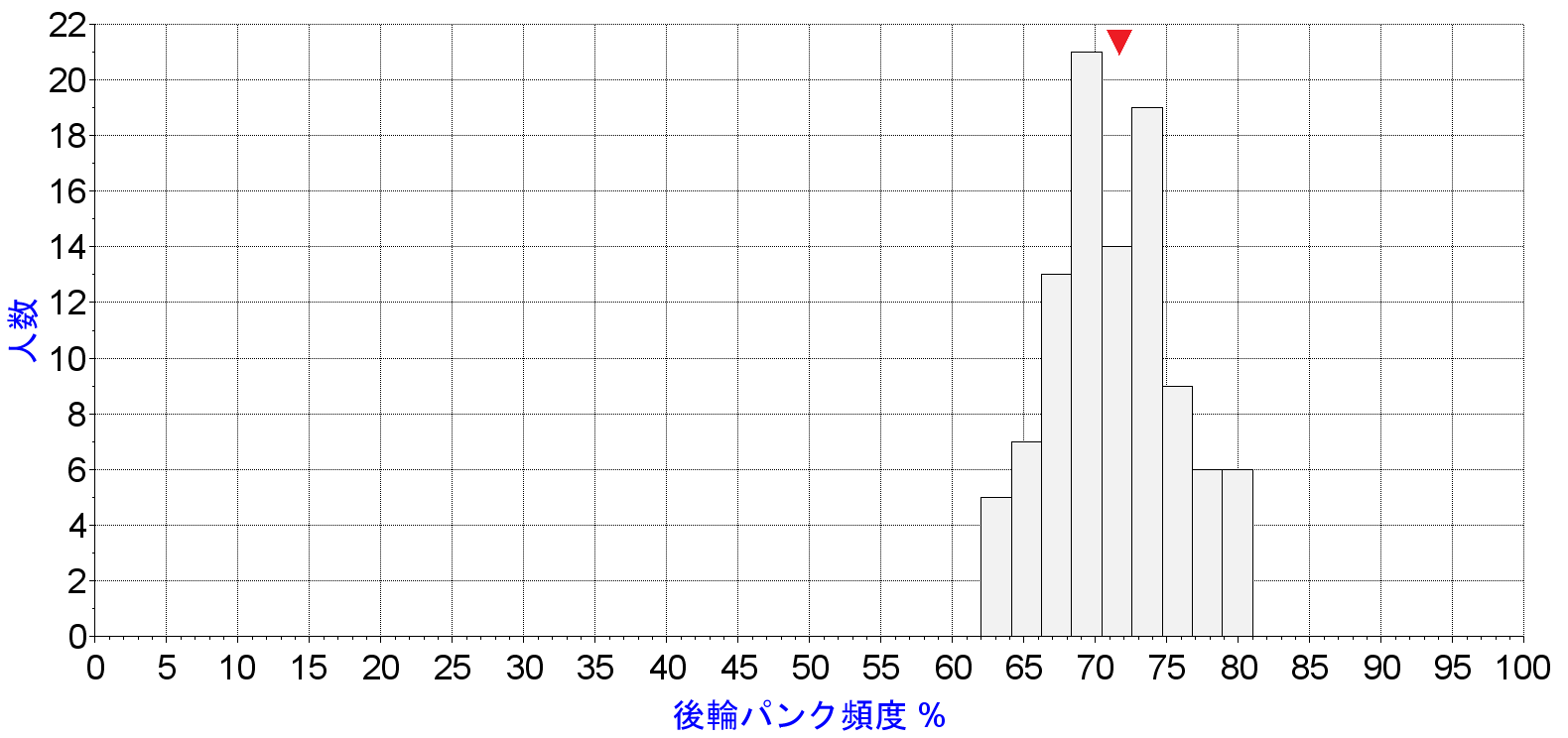
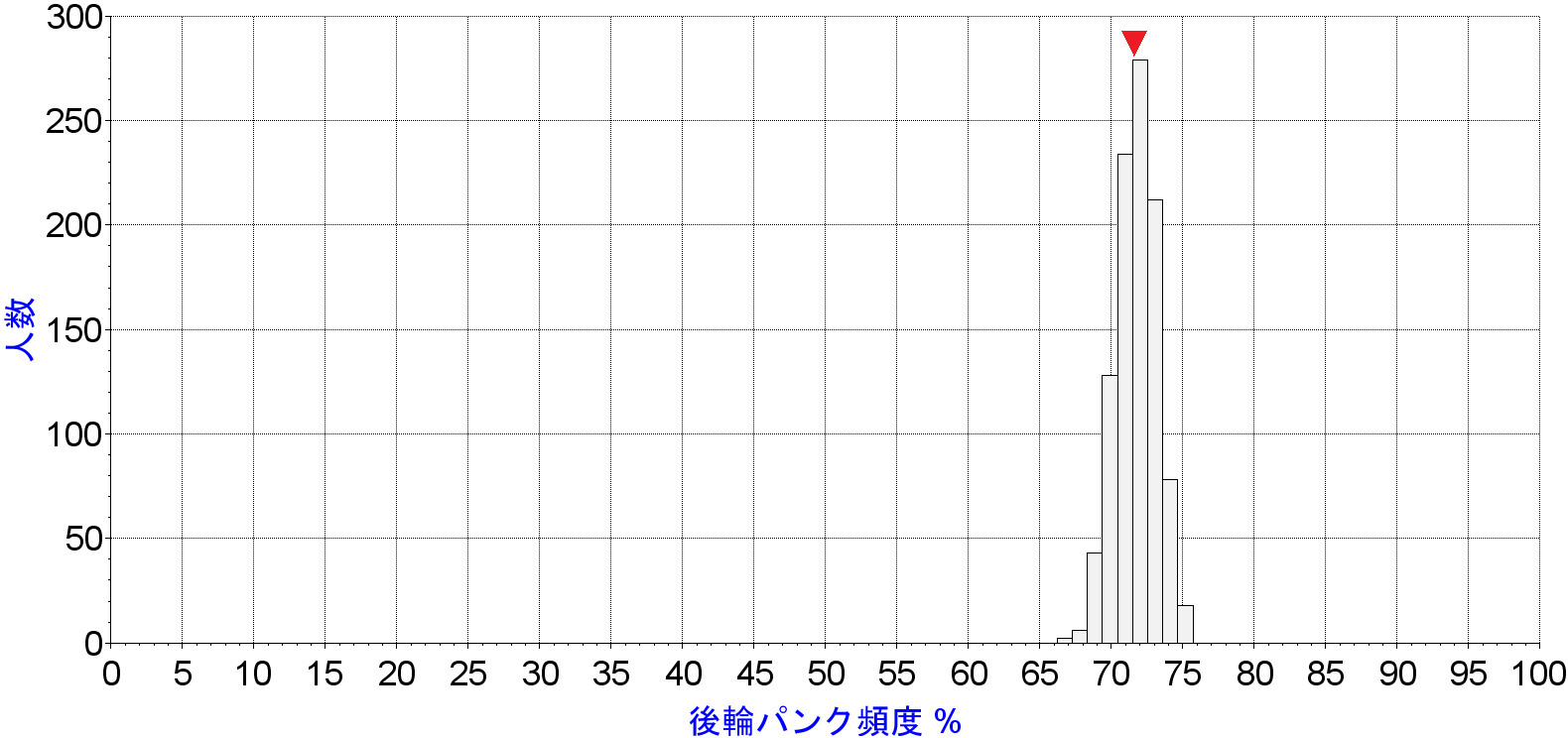
100回パンク後のリアパンク頻度の分布を、9本の棒グラフに分割して表示しています。横軸がリアタイヤのパンク頻度%、縦軸は、各棒グラフに所属する人数です。棒の高さを合計すると100人になります。
全体の分布は20%程度の幅があるとはいえ、70から75%付近の人数が多いことがわかります。赤い三角記号の位置が71.7%です。100人がそれぞれ100回パンクする、つまり10000回のパンクデータをまとめると、ようやく、70%前後付近にピークがありそうだ、ということが見えてきます。
1000人がそれぞれ1000回パンクする場合
パンク回数が増えると、リアタイヤのパンク確率が71.7%に近づく傾向があります。となると、1000回ならさらに近づくことでしょう。どうなるでしょうか？
面倒なので、1000人が1000回パンクする（笑）、という机上実験を行ってみます。
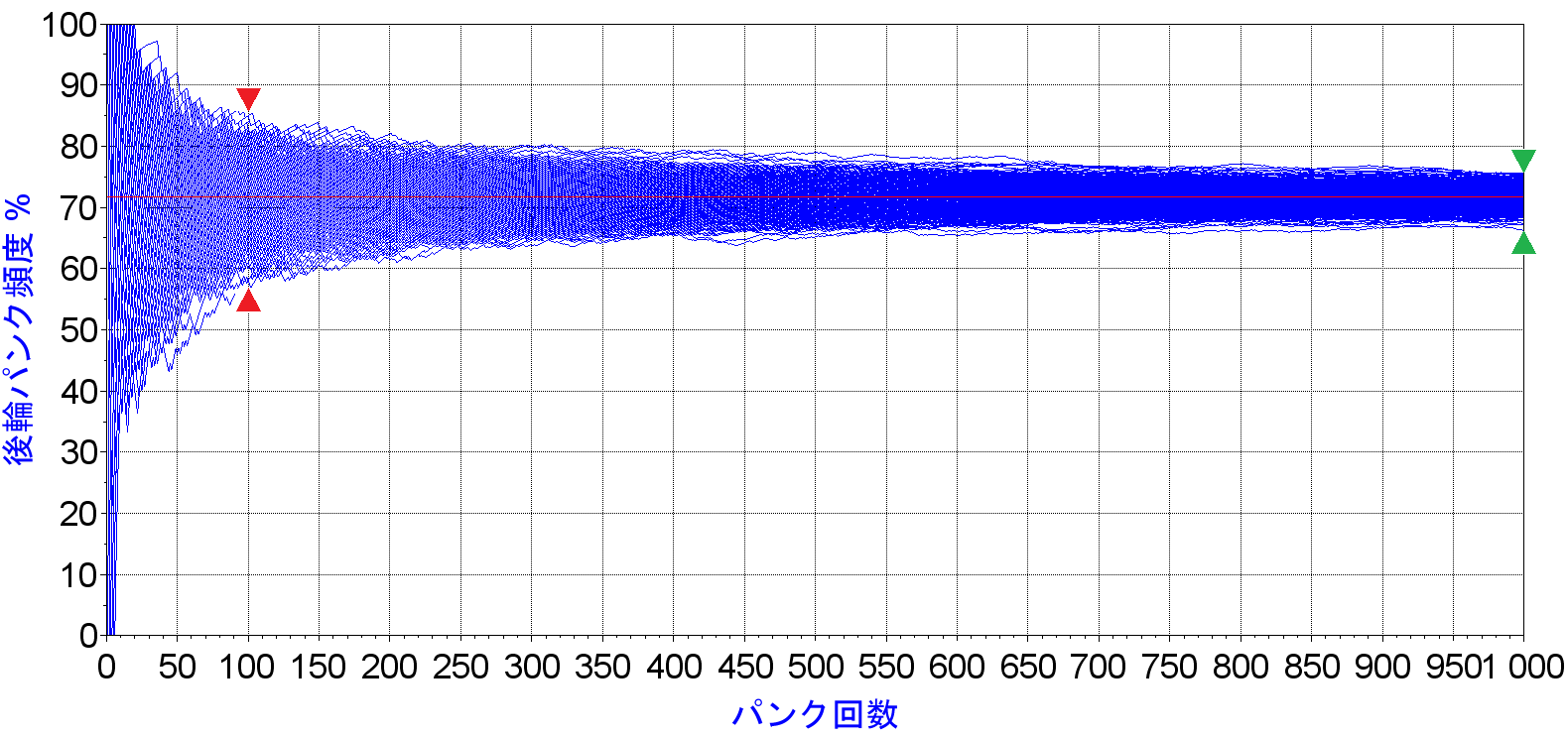
結果がコレ。
1000人がそれぞれ1000回パンクした場合のリアタイヤのパンク頻度推移
1000回のパンク履歴を1000人分まとめて重ねてグラフ化していますが、ちょっと壮観ですね。このグラフの100回パンク時点での拡がり幅を赤い三角記号で示し、1000回時点での拡がり幅を緑の三角記号で示しています。明らかに1000回時点での拡がり幅が狭くなっています。半分以下、でしょうか。
このグラフのパンク1000回目で、1000人はそれぞれ、リアタイヤのパンク頻度がどこに落ち着いているのか？その分布を確認してみます。それが次のグラフ。
1000人がそれぞれ1000回パンクした場合のリアタイヤのパンク頻度推移
1000回パンク後のリアパンク頻度の分布を、9本の棒グラフに分割して表示しています。全体の分布幅は10%以下となり赤い三角記号の位置で示した71.7%に近い位置にピークが来ているようです。1000人がそれぞれ1000回パンクする、つまり100万回（！）のパンクデータをまとめると、ピーク頻度が真値である71.7%に、かなり近づきました。
それにしてもですねぇ。
100万回もパンクしたのに、リアタイヤのパンク頻度ピークは72%近辺にありそうだ、という程度のことしか、結局、言えないというわけです。
つまり、確定的なことを言う、ということが、場合によっては非常に難しい、ということが何となく理解されるのではないかと思います。
「オレ最近、フロントが4回連続してパンクしてるけど、完全に呪われてるぜ、どうすればいいんだよ？」
これに対する回答としては
「頻繁にパンクしてるんなら、リムテープがねじれてるとか、中に何か挟まっているのかもよ？」
という整備上の指摘と、
「でも、滅多にパンクしないんでしょ？所詮、パンクなんてそんなもん。そういうこともタマにはあるぜ、気にすんな！」
のような、確率過程を前提とした回答などが考えられますが、前者の回答のほうが多少、気が利いているかも知れませんね。
COVID-19抗体検査結果0.7%の意味
東京大学アイソトープ総合センターによると、5月、東京都内の医療機関で採血された合計1000例につき、新型コロナウィルス（COVID-19）の抗体定量測定を行った結果として、7名の陽性判定が得られているそうです。
出典 https://www.ric.u-tokyo.ac.jp/topics/2020/ig-20200604.pdf
さて、東大のこの発表を読んで、どこかの新聞記者が次のような一文を書いたとしましょう。
1000名分の定量検査で7名が抗体陽性判定、つまりこの検査での陽性率は0.7%。したがって5月のこの測定時点での東京都内の抗体陽性者数は、東京都の人口1400万の0.7%なので約10万人と推定される。
この文章の前半は、この検査、という限定を設けて0.7%と述べており、正しいことを言っているのですが、後半は、完全に飛躍しています。たったの7人しか陽性者が確認されていないのに、そのまま0.7%を東京都の全人口に当てはめるのは、非常に雑な話です。上のパンクの話から、そこはすんなり理解されると思います。
さて、5月に行われた1000人分の抗体定量検査の結果0.7%が、そのまま都内全体の抗体保有率（陽性率）であると仮定してみましょう（仮定ですヨ！）。
で、パンクの時と同じように計算してみましょう。つまり、1000人の抗体検査プロジェクトを1000回実施し（100万人検査！）、それぞれのプロジェクトの抗体検査が1000人に到達するまでにたどる陽性率の推移を、1000プロジェクト分まとめて重ね描きしたのが次のグラフです。赤線が仮定した抗体保有率0.7%です。
1000人の検査を実施するプロジェクトを1000回実施した場合の各プロジェクトの抗体保有率率推移
1000人に達した時点でも、実に0%から2%近くまで抗体保有率がばらつきます。薄目にして眺めると、赤線の0.7%に近づいていますが。
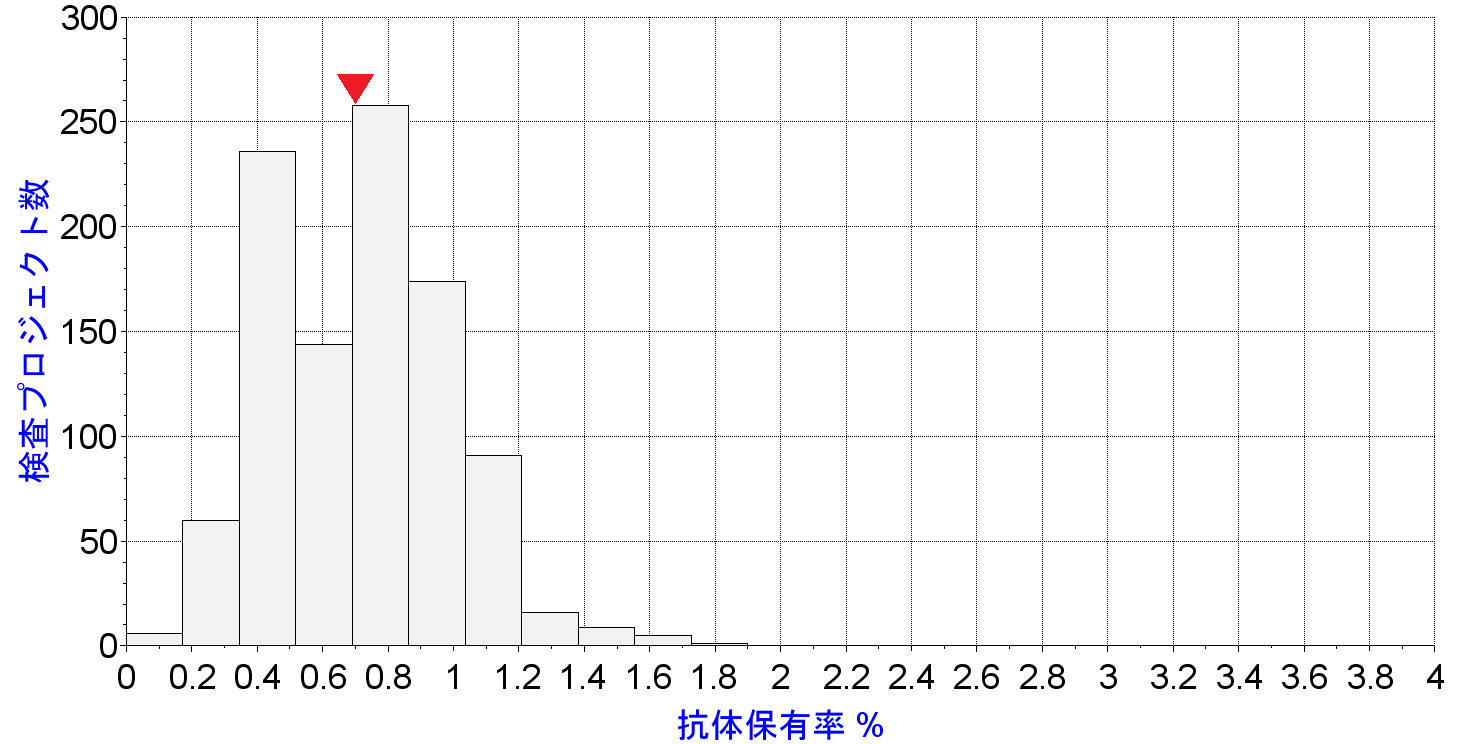
では1000人時点での抗体保有率の分布はどうか？次のグラフです。
1000人の検査を実施するプロジェクトを100回行った場合の抗体保有率分布
1000人検査時点での抗体保有率バラつきを9分割して棒グラフで示しています。各棒の数値の合計はもちろんプロジェクト数で、1000回です。1000人検査プロジェクトを1000回実施すると、真値として仮定した赤い三角記号の0.7%とグラフのピークが近そうだ、ということがわかります。
東大の発表数値である、陽性者数7名、その人数は1000人中7名だから0.7%である、という内容は、単に事実を述べただけで、全く誤解の生じる隙などありません。しかし、この発表を誰かが勝手に、
都内の抗体保有率は0.7%だから、5月のこの測定時点での東京都内の抗体陽性者数は、東京都の人口1400万の0.7%なので約10万人と推定される
などと解釈して解説したりすると、誤解の元にもなりかねません。陽性者数が1000人中400人だった、ということであれば約40%として、そのまま人口比換算しても比較的安全な議論が可能ですが、7人では、これはもう、如何とも言い難い。
ひとつのデータをどう解釈するか、というのは、時に極めて難しく、迂闊なことは言えない、というわけです。
抗体保有率とパンク頻度、何だか似ていると思いませんか？コロナ報道を見る目が変わっちゃいそうですねぇ！
まとめ
- 単純な確率計算でパンク頻度を机上実験したところ、仮定したリアパンク率に対して、100回パンク時点で実に±10%程度の幅が見られた
- 新型コロナウィルス（COVID-19）の抗体定量測定結果を引用して1000人検査プロジェクトを机上で1000回実施したところ、抗体保有率に大きな広がりが見られた
- ひとつのデータをどう解釈するか、というのは、時に極めて難しい
おまけ
今回の計算はフリーソフトscilab（windows版）を使っています。以下のリンク先からScilab 6.1.0をダウンロードしてインストールすればすぐに使えます。（※64bitマシンの方は64bitマシン用を選んでください）
Scilabを起動して、文字を打ち込む画面（コンソール）が現れたら、そこに次の // で挟まれた部分をコピペすれば、一番最初のグラフを得ることができます。
是非どうぞ！！
//
scf()
for J=1:1:1 //試行人数
P=0;
for I=1:1:100 //パンク回数
R(I)=rand(I);
if R(I)<=0.717 then P=P+1; //I回目のパンクが後輪である場合、後輪パンク回数を1回加算
elseif R(I)>=0.717 then P=P; //I回目のパンクが前輪である場合、後輪パンク回数の1回加算なし
end
Probability(I)=P/I*100; //I回目のパンク時点までの総計で、後輪がパンクした率
P_final(J)=Probability(max(I)); //最終回パンク時点までの総計で、後輪がパンクした率
end
plot2d(Probability,rect=[0.001,0,101,101]),xgrid,xset("font size",6)
plot(Probability,'.',"color", "blue"),xgrid,xset("font size",6)
xlabel("パンク回数","fontsize", 6, "color", "blue");
ylabel("リアタイヤのパンク頻度 %", "fontsize", 6, "color", "blue");
end
plot(Probability*0+71.7,"color","red"),xgrid
//
▼ GlennGouldさんのその他の自転車考察記事はこちらかも読めます
