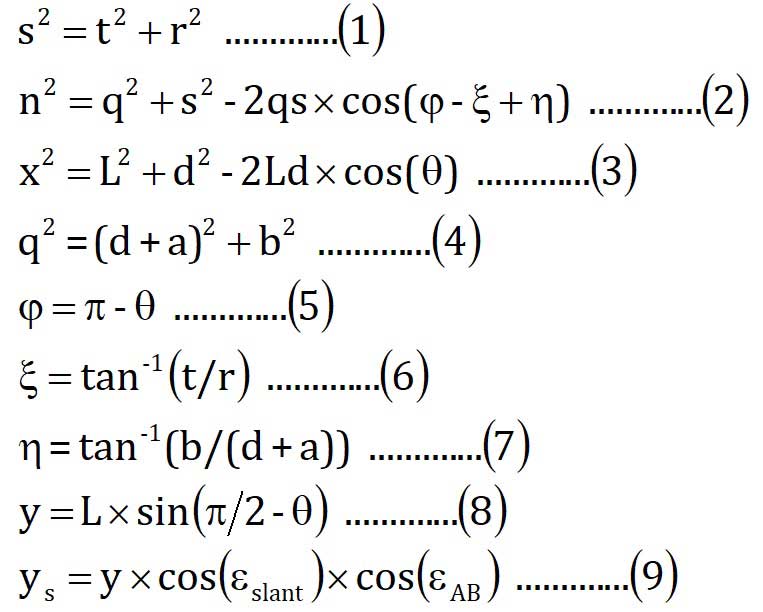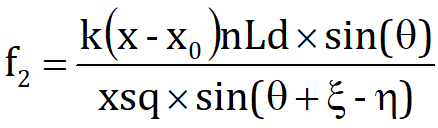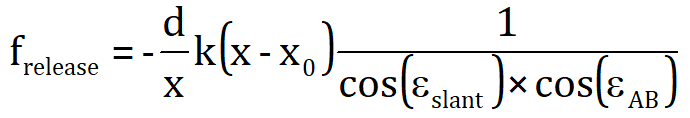現代のリアディレイラーに、もれなく見つけることができる「平行四辺形」。次の画像はシマノのRD-7400(1984年発売)です。旧式モデルですが、四辺を連結するピンが良く見えるため、平行四辺形がはっきりわかります。その平行四辺形を模式的に重ねてみました。
RD-7400のパンタグラフの平行四辺形とB軸、P軸 (※テンションプーリーをオリジナル10Tから11Tに変更しています)
4本のピンでつながれた四辺のリンクが平行四辺形を形成し、これが変形することで変速を行う、というのはみなさん、よくご存じの通りです。なお、ディレイラー本体をフレーム側に取り付ける軸をB軸、プーリーケージをディレイラーに取り付ける軸をP軸と呼ぶことが多いようですが、これも載せてみました。
リアディレイラーの絶妙な動き。
どんな動きをしているのか、じっくり眺めたこと、ありますか？
今回は、ディレイラーには必要不可欠な、この「平行四辺形」について少し考えてみようと思います。
えっ、そんなことして何がわかるかって？
リアディレイラーの動作を形作っている主役がこの「平行四辺形」なのだ！
ということがわかります。そして、リアディレイラーの構造に対する造詣が深まります！
「それ誇張だろ。造詣じゃなくて妄想じゃねぇのか？」
まあ、その可能性は大ですが、しばらくお付き合いください！！
平行四辺形の変形を目で確認してみよう
最近のシマノのリアディレイラーは、先ほど申し上げたB軸とP軸の位置だけを取り上げても、従来からの大きな変化が見られて実に興味深いですよね。実は、これには非常に大きい理由があるのではないかと考えているのですが、大変長くなるので別の機会にあらためてお話したいと思います。
いずれにしても「平行四辺形」がディレイラーの中心骨格です。というわけで、
- リアディレイラーの動作を形作っている主役がこの「平行四辺形」であることを理解する
- リアディレイラーの構造に対する造詣を深める
という2大課題(2大妄想)に挑みますが、
まずはウォーミングアップです。平行四辺形の変形を実際に目で確認してみましょう！
次の画像はリアディレイラーを下側から覗き込んだところです。ディレイラーはShimano Dura-Ace RD-7800(2003年発売)です。
RD-7800のトップ状態(左)とロー状態(右)
左がトップギヤの位置、右側はローギヤの位置での状態を示します。黄色い線で示した平行四辺形の平面をそれぞれ正面から捉えています。ディレイラーを形成するこの平行四辺形が、電車のパンタグラフのように変形して変速が行われます。
平行四辺形の過激な変形をご確認ください。それにしても昔のディレイラーは平行四辺形がわかりやすいですねぇ。
一方、こちらはシマノのアルテグラRD-6500(1997年発売)です。おやっ？平行四辺形が78デュラよりもすこし長いようですね。
RD-6500のトップ状態(左)とロー状態(右)
変速機のパンタグラフ機構では、フロントもリアも4辺のリンクをピンで連結した構造を持ちます。
「4つのリンクをピンで連結した構造」、これは機械の世界では｢4節リンク｣と呼ばれています。リアディレイラーの4節リンクは、複雑な動作を示すいびつな四角ではなく、キッパリと平行四辺形になっているように見えます(もしかしたら設計数値は微妙にいびつなのかも知れませんが)。というわけで、4節リンクの中では最も単純な形式となっています。
昔の手動ミシンの足踏み機構、クルマの「ダブルウィシュボーン・サスペンション」や「アッカーマンステアリング機構」などなど、4節リンクはいろいろなところに使われていますが、自転車関連で珍しいところでは、トランスミッションに応用した本田技研のダウンヒルマシンRN01(の初期版)という、実戦投入された(そしてあっという間に消えた)、伝説の超仰天機構もありました…おおっと、脱線しそうになっちゃたぜ！RN01のトランスミッションの話も別稿で。
以上でウォーミングアップ完了！！
動きを抽象化してみよう
さて、ここからが本番です。この章は平行四辺形の動きを一気に俯瞰するための下準備です。
先ほどの平行四辺形が動作する画像はRD-7800とRD-6500のパンタグラフを下から覗いたものでしたが、上側から見た様子を模式的に表わしたのが次の図です。
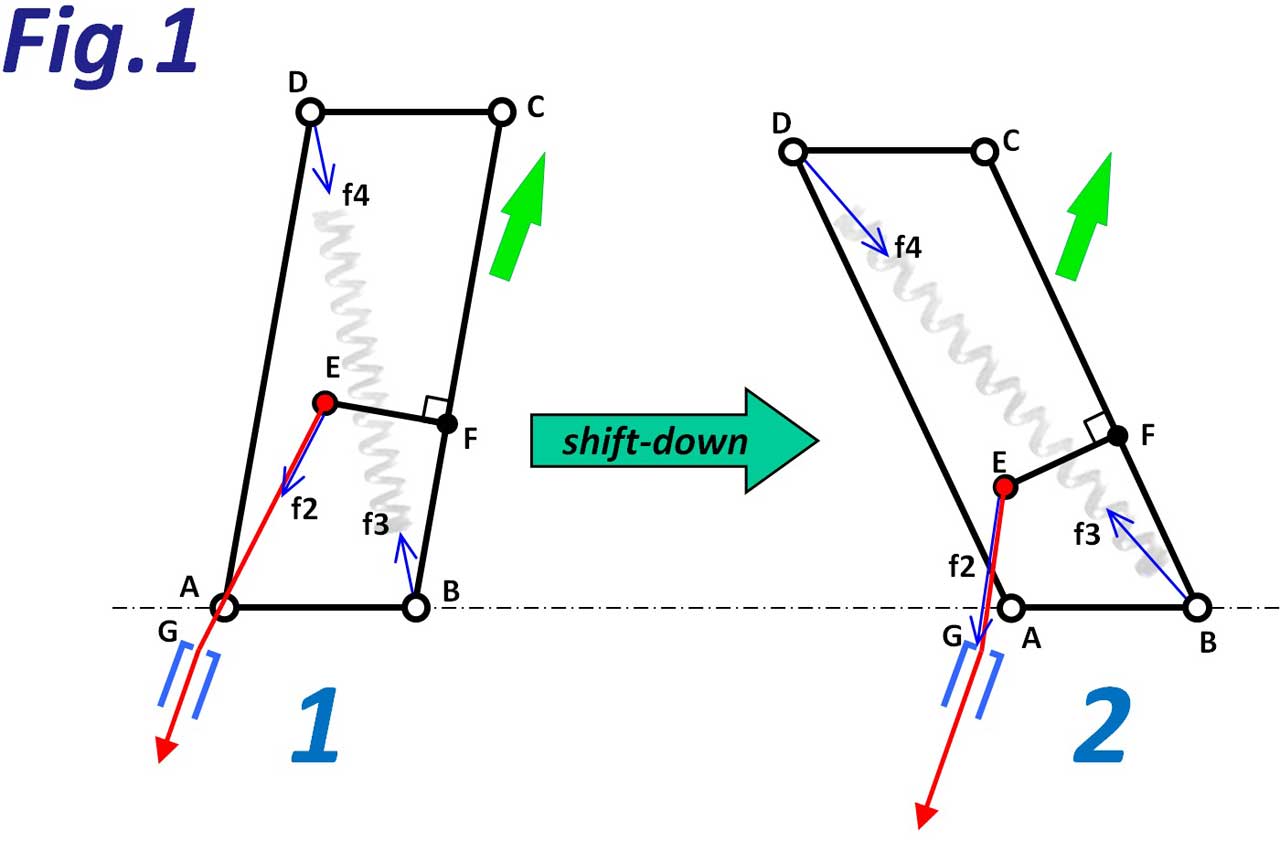
平行四辺形ABCDのうち、辺ABは、最初に説明した＜B軸、P軸＞のB軸を介してロードフレームのリアエンドハンガーに接続されます。また、対角線BD上には、図のように縮もうとするスプリングが敷設されており、平行四辺形をトップ側に戻そうとする力を発生しています。
ABCDの各点以外に、EとFとG点を定義しています。Eはインナーワイヤーがディレイラーに固定されているポイント。Fは、Eから辺BCにおろした垂線が交わるポイントです。Gは、アウターワイヤー受けからインナーワイヤーが出てくるポイントです。なお、辺ABはフレームのリアハンガー面に対して微妙に直角ではないようです。
斜め右上を向いている黄緑の矢印ですが、これは自転車の進行方向です。次に、赤線で示したのがワイヤーです。このワイヤーを引っ張ると、ワイヤー固定端であるE点が、アウターワイヤー受け部のG側に引き寄せられ、左の図が右の図のように変化し、ロー側への変速が行われるというわけです。
ロー側に変速すると対角線BD上のスプリングが無理やり引き伸ばされますので、力を示す矢印の大きさf3 (=f4) が増大します。
動きを計算してみよう
この章ではこの平行四辺形の動きを、エクセルなどを使って計算してみます。計算することで、何となくイメージしていたことが明瞭になります。
また、共通言語である数式を使うため、再現性が確保され、同じ認識の下で議論をすることが可能になり、勝手な思い込みの沼に嵌ることを防止することができます。
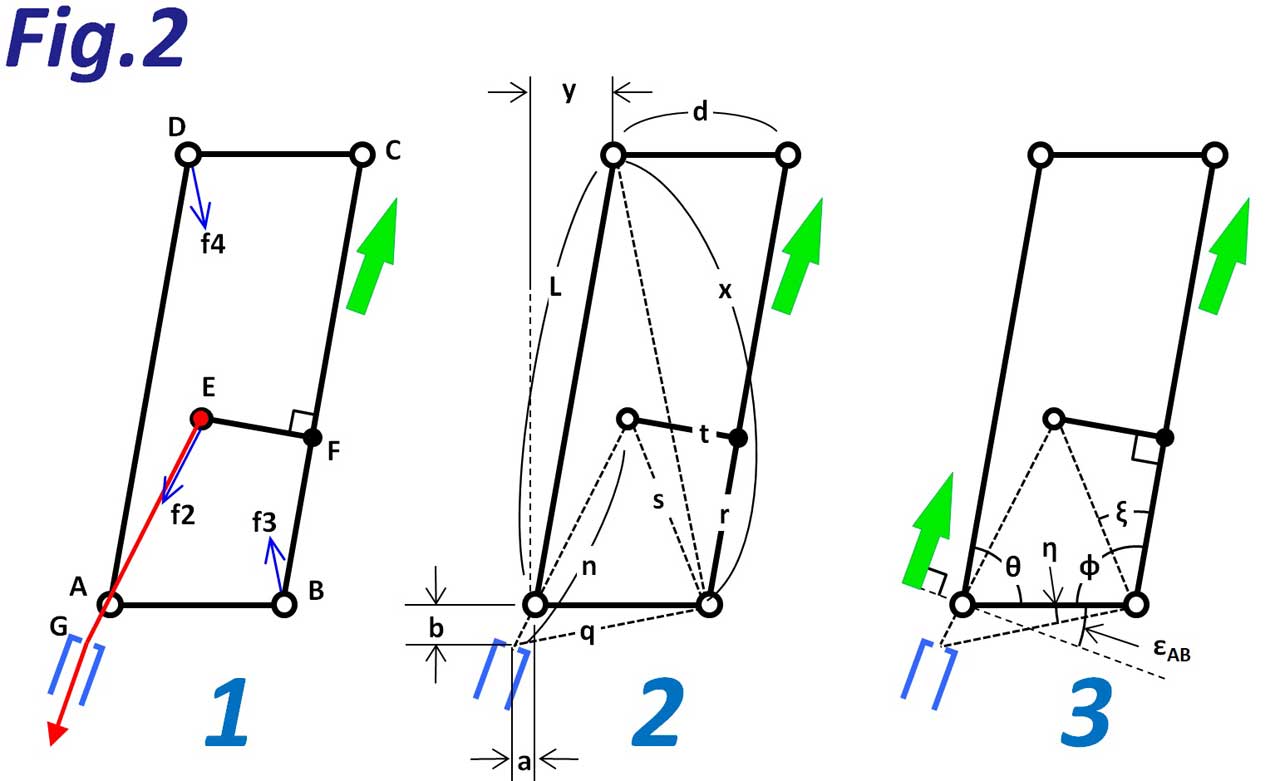
というわけで式を作るのですが、事前作業として、次の図のように線を加えたり、長さや角度の名前を付けておきます。
いちばん左の図はFig.1の左の図の再掲。2番目は「各辺の長さ、また、追加した補助線の長さ」を示します。3番目は「各部の角度」を示します。
あと忘れてはいけないのが、この平面図ではあらわれない「スラント角度εslant」です。トップからローに向かって変速すると、ガイドプーリーがスプロケの歯先に沿って動きますが、この動作のために、平行四辺形がB軸に対して傾いて設定されています。この角度がスラント角度です。
RD-7400のスラント角度 εslant
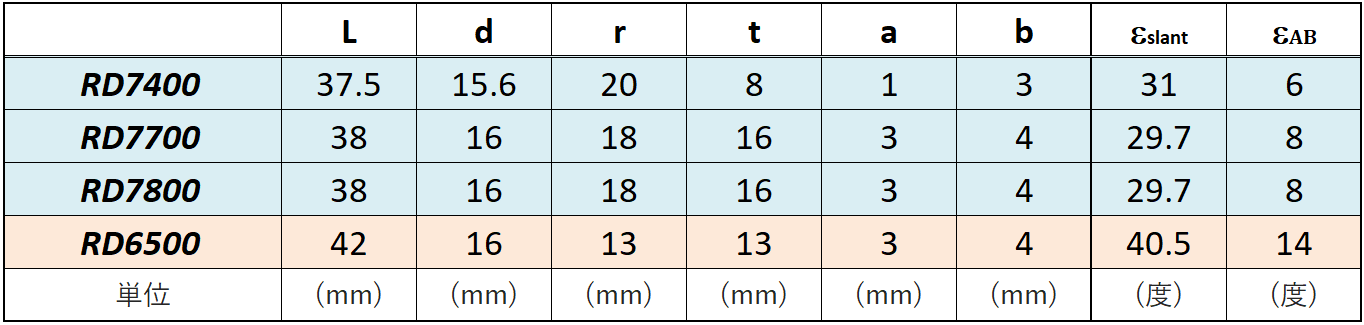
Fig.2で命名した各部の長さL、d、r、t、a、bと角度εslant、εABの実例を次表に示します。これだけ定義できれば、ワイヤー引き量に対する平行四辺形部分の幾何学的な動きは式を使って完全に記述されます(撓みとか捻じれは除いて)。
各部の長さと角度の実測値事例(ただし精度は期待しないでね！)
初代インデックスシステムのRD-7400とそれ以降のディレイラーの違いが際立っています。また、アルテグラRD-6500のスラント角度の大きさが目を惹きます。
アルテグラの祖先はシマノ600EX(1980年発売)、さらにはシマノ600(1976年発売)ですが、もともとツーリング用途のモデルでした。もしかしたらその名残かも知れません。そして、ワイヤー固定部に伸びる腕の長さtがRD7400では随分短いというのも特徴です。
RD-7700以降ではワイヤー固定ボルトの六角ヘッド部がパンタグラフ機構の外側に設置されますが、RD-7400では内部に隠れる形で内向きになっています。そのためにtを大きくとることができなくなっている、というのが理由でしょう。
ところで、これらの数値は、最近すっかり手元が見えにくくなってきた私がノギスを使ってチョー適当に採寸した結果です。また、スラント角度や辺ABの角度は、目分量＋状況証拠で固めるというテイタラクなのであしからず！
というわけで、Fig.2で示した関係を式で示します。
リアディレイラーの基本式
高校の数学が出てきてしまいましたがご容赦ください。
式(8)のyというのはFig.2の中のD点の横方向の動きを示しています。これは平行四辺形の平面内での話なのですが、角度εABとεslantを使うと、式(9)のysのようになり、ガイドプーリーが動く水平方向成分の位置関係を反映させることができます。
基本式はこれですべてなので、あとは角度θをだんだん大きくしてロー側に変速させれば、ワイヤーの引き量やガイドプーリーの水平方向の動作がどんな風に推移するのかがわかります。ちなみに10速でトップエンドからローエンドまで動いた時、ysの変化量は35.55mmとなります。
以下で、RD-6500の数字を使って計算した結果を視覚的に確認してみましょう。
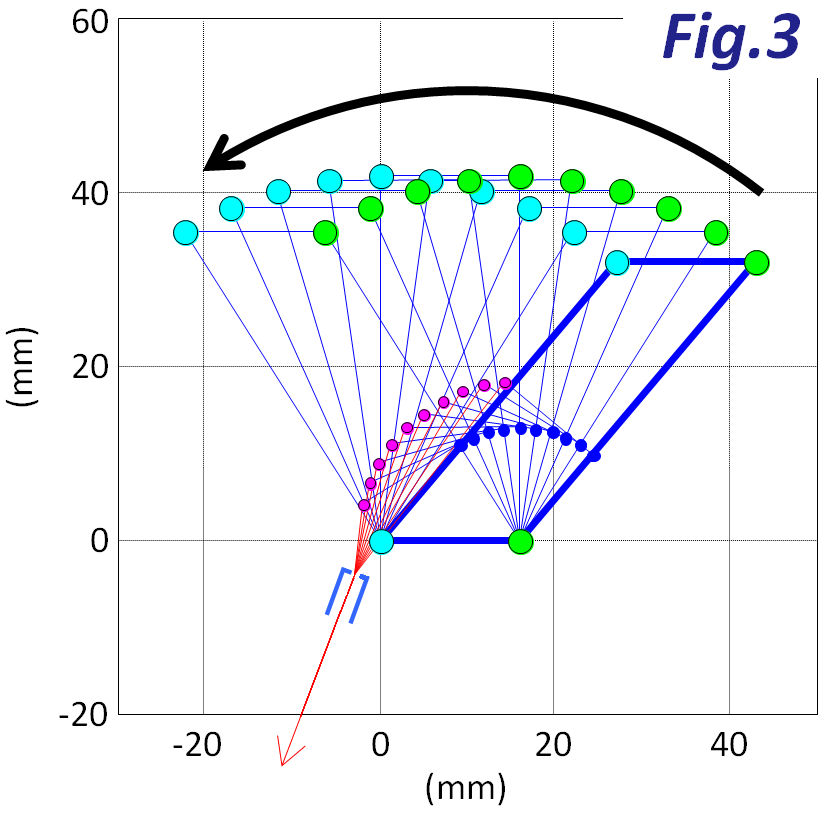
まず、ワイヤーを引っ張ってみます。Fig.3のように平行四辺形がグワ～ンと変形して先端部が円弧を描きます。そりゃそうだろ、という感じです。
こんな感じで平行四辺形が動く
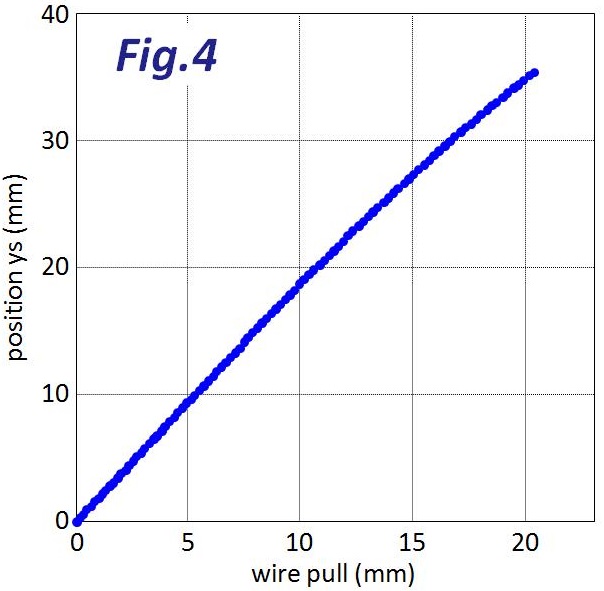
次に示すFig.4は、トップ位置からのワイヤーの引き量に対するガイドプーリーの横方向の移動量です。ワイヤーの引き量に対してysの動作が直線ではなく、微妙に曲がっています。ロー側に近づくほど、ysの動作が鈍くなり、ワイヤーを余計に巻きあげないと変速しない、ということがわかります。
ワイヤー引き量に対するプーリー移動量ysの関係
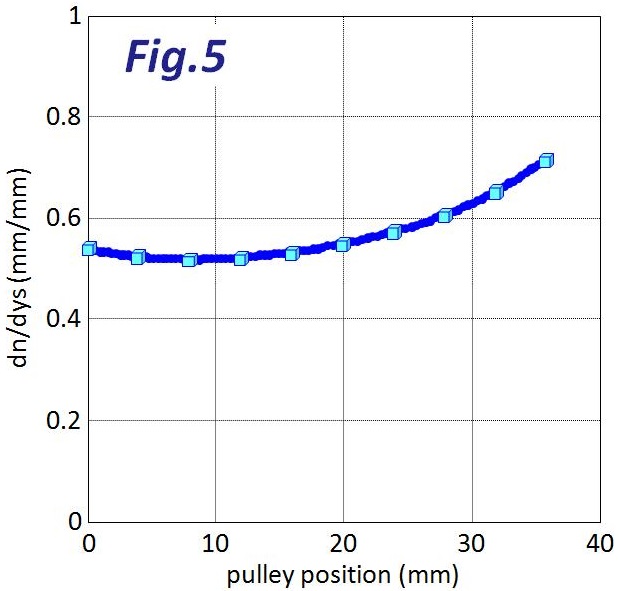
Fig.5も同じことを示していますが、こちらはプーリー位置ysの変化に対するワイヤー引き量の変化の割合が、プーリー位置でどのように変化するかを示しています(実は単にFig.4の微分値の逆数)。ワイヤーを引かなければならない量がロー側になると段々増えていくということを示します。
Fig.4の微分値の逆数
ワイヤー引き量を変えるとどうなるか？
ところで、インナーワイヤーを固定する位置を決めるのはrとtです。
となると、RD-6500のrとtを変えると、ワイヤー引き量に対するプーリー移動量はどうなるのか？という疑問が湧きます。
まず、rが8mmから42mmまで4種類の場合についてFig.6に計算結果を示します。青のr=13が実際の製品の値です。rを小さくすれば同じワイヤー引き量でプーリー移動量を大きくすることができる、ということになります。
rとワイヤー引き量に対するプーリー移動量ysの変化
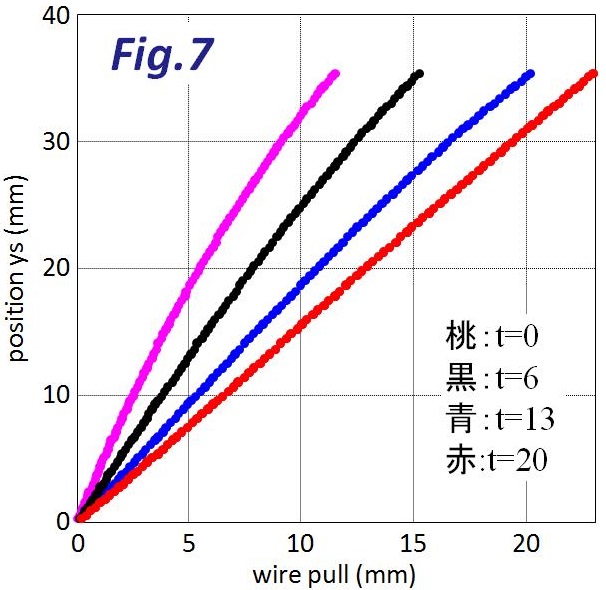
次にtの長さ。0mmから20mmまで4種類についてFig.7に結果を示します。青のt=13が実際の製品の値です。tを小さくすれば同じワイヤー引き量でプーリー移動量を大きくすることができる、ということになります。
tとワイヤー引き量に対するプーリー移動量ysの変化
ということはどういうことでしょうか？
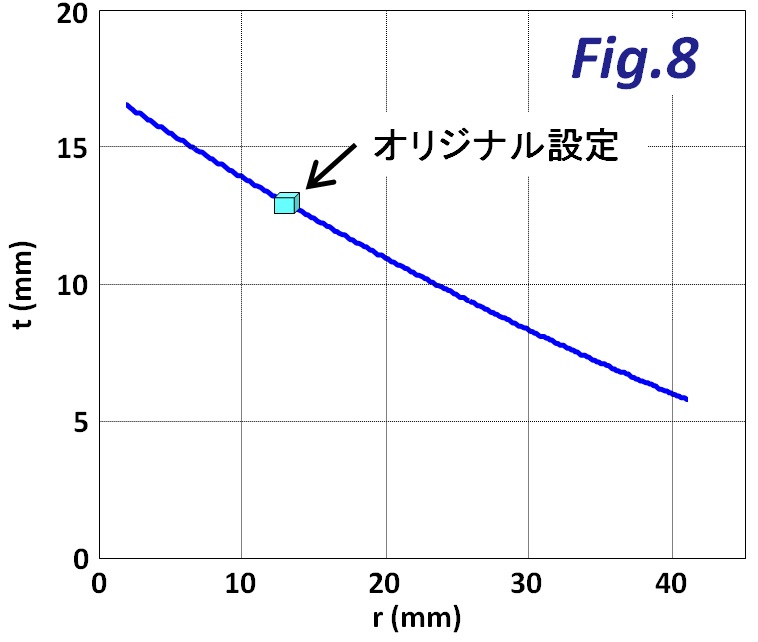
そうです。ワイヤー引き量とプーリー移動量を同じ関係に維持するためには、rとtがある関係を保つ必要があるということになります。トップからローまで変速するときに必要なワイヤー引き量とプーリー移動量を、現実の製品のそれと同等に拘束した条件で解を導出すると、Fig.8 を得ます。
ワイヤー引き量とプーリー移動量を同じ関係に維持するときのrとtの関係
つまり、rが遠くなったらtを短くすれば、トップからローまでのワイヤー引き量とプーリー移動量を同じ関係に維持することが可能になります。図の中で水色のサイコロ図形で示したのがRD-6500 のオリジナル値r＝13mm、t＝13mmの場合ですが、このrとtの組み合わせ以外にもFig.8 に示したような数値の組み合わせが許容されます。
これはある種の設計自由度を表現しています。オリジナルの数値は、実物としての実現性、そして軽量化や強度、デザイン性との兼ね合いで決まっているのでしょう。
ちょっと前に戻ってFig.4とFig.5をもう一度見ると、シマノ・インデックス・システム(SIS)のワイヤー巻き上げ量も、各段で等量ではなくFig.5のように微妙にロー側で増大しているはずだ、と気が付きます。ということは、隣の段に移る際に引かなければならないワイヤー長さは、段ごとに変えなければならないはず、です。
そこで確認です！ 10速のWレバーSL7800をパキパキやって、各段のレバー角度を測ってみましょう！
パキパキパキパキパキパキパキパキ、パキッ・・・(パキが9回！)
10速SIS Wレバーの各段での位置
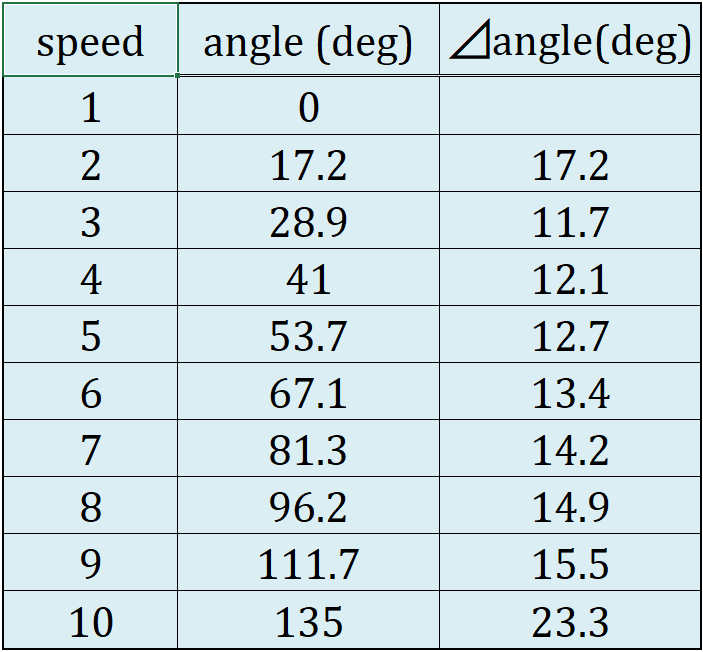
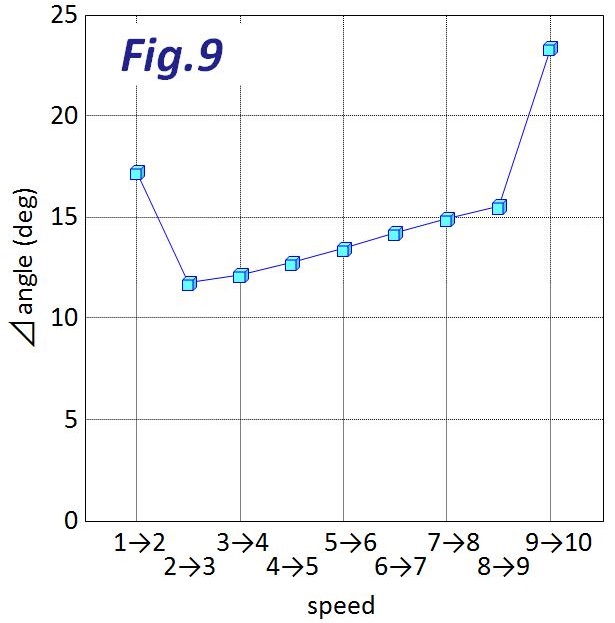
次の表はトップからロー側までWレバーをSIS動作させた時の角度と、各段の間の角度差を示しています。グラフは角度差を示しています。2段目から9段目までは角度差が緩やかに増大しますが、これはFig.5から考えると、おおーっ、なるほど！という感じです。
WレバーをSIS動作させた時の角度と、各段の間の角度差
WレバーをSIS動作させた時の各段の間の角度差
ところで、1段目の位置決めは、ディレイラー自身のストッパーで決まるため、ワイヤーにはわずかな緩みが生じますが、シマノ変速機の取説に書かれているように、アウターワイヤー側に付いている調整ボルトを指で回してこの緩み量を微妙に修正します。1段目から2段目の角度差が17.2度とあからさまに大きいのはこれが理由です。
ロー側の最終角度差23.3度は？
トップ側がディレイラー自身のストッパで位置が決まっているのなら、ロー側も同じらしい。実は、ワイヤーを引いてローエンドのストッパに突き当たり、さらにワイヤーを引き上げて10段目のSISにパキッ！と入ってWレバーが所定位置に収まります。ローエンドだけワイヤー張力がグン！と上がっています。ワイヤーを指で弾いて音を聞くと、ローに入れるときだけ音高がグンと上がります。それは一聴瞭然です。
ところでRD-7400ですが、計算上ではどうやら10速SISで設定される引き量に対してガイドプーリー動作量が大きすぎて、10速SISにはシンクロしないと推測されたのですが、実際にWレバーSL7800で引いてみると、ほぼ予想通り、8速目のレバー位置で9速のスプロケ位置まで行ってしまいました。
というわけでRD-7400は10速SISにはシンクロしません。しかし、フリクションモードを持つWレバーで変速すれば、今でも十分使えることでしょう。
さあ、ここまでいかがでしょうか。平行四辺形だけをとりあげても、
リアディレイラーを特長づけるパラメータは相互に関連していて、最適化は一筋縄ではない
という気配が濃厚ではないでしょうか。逆に見れば、設計自由度がかなり大きい、ということも出来ます。明確な方針のもとに開発を進めないと、大きな設計自由度の中で性能と意匠を満足するパラメータの組み合わせを求めて迷走し、遭難する可能性も大でしょう。リアディレイラーは奥が深そうですね！
リアディレイラーにまつわる3つの力
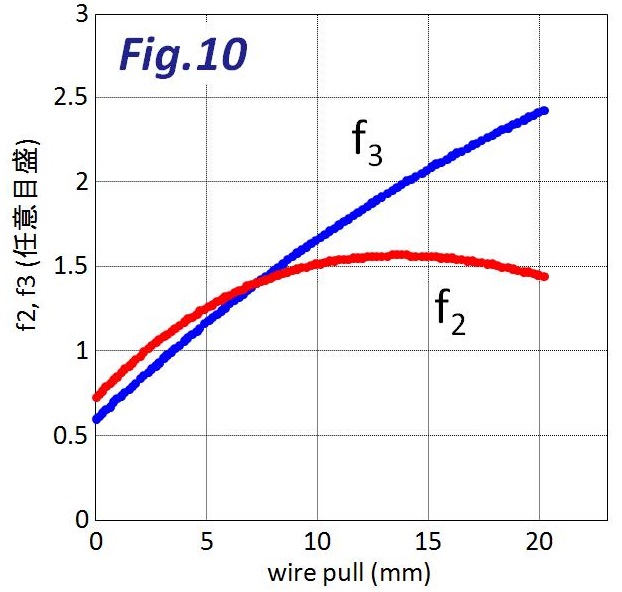
せっかくですので、リアディレイラーにまつわる次の3つの力を算出してみます。
- ワイヤーを引く力「f2」
- 平行四辺形内部のスプリングの力「f3」
- ディレイラーが自力でトップ側に戻るときにチェーンを脱線させる力「frelease」
えっ、なぜそんなことするかって？
他でもない、メカとエレクトロニクスが一体化した電動ディレイラー（メカトロディレイラー）を構成する場合に、例えばワイヤーを引く力f2というのは、モーターが発生するべきトルクに直接かかわってくる力です。
「オレの旧デュラを電デュラに改造しようかな～」
などという妄想を最短距離で実現するためには、色々と下ごしらえが必要になるかと思いますが、f2の算出はその一環となることでしょう。だからやるんです！(笑)
もちろん、他にもいろいろ知らなければならない数値や電気モーターの知識などがありますが、少なくともこのf2がわからずに真っ当な電動変速機の設計など到底、できません。
「じゃ、アンタは旧デュラを電デュラに改造するのかヨ！？」
と言われると…そうではないので、まあ、興味本位ではありますが、とにかくやってみましょう！
ワイヤーを引く力を手で感じてみる
さて、「ワイヤーを引く力f2」のイメージを掴むために、手勘で探りを入れてみました。リアホイールを外し、フリクションモードのWレバーの固定力をユルユルにしてトップからローに向けてディレイラーを動かしてみると…
ディレイラーのスプリングが伸ばされてスプリングの力f3は順調に大きくなるはずですが、一方、手勘では、f2の増大が指にあまり伝わってきません。ワイヤーを指で弾いて弦の共鳴音を確認すると、ロー側に向かって音高がはっきり上昇していくような感じもない。意外とf2の増大は穏やかなのかも知れません。
ワイヤーを引く力を算出してみる
というわけで、ワイヤーを引く力f2を算出してみましょう。
ここでは、エネルギー保存則を使いました。すなわち、
ワイヤーをf2で引っ張るときの仕事は、スプリングに与えるエネルギーの増大と釣り合う
という関係を使ってカンタンに算出します(というか、力のつり合いをマジメに考えるのが面倒なので裏口入学敢行！)。
実際には節部やワイヤーのしゅう動部、特にG点での摩擦力を考慮しないといけませんが、とりあえず無視して考えます。式の経過は省略します(もし知りたい方がおられたら質問大歓迎)が、f2はこんな風になります。
ワイヤー引っ張り力f2の式(ただし各種摺動抵抗を無視)
ここで、スプリングの長さxの値として、Fig.2で示した対角線BDの長さをそのまま使っていますが、これは便宜上そうしただけです。また、スプリング単体の長さ、つまり外して放置した時の一番短いスプリングの長さx0も具体的にどういった値を与えればよいのか、そしてスプリング定数kの値も、スプリング単品を取りだしていないのでわかりません。ディレイラーの状態でスプリング定数やセット荷重を計測する方法が無いわけではないのですが。
というわけでこの稿では、適当にkとx0を定めていますので、力の絶対値ではなく、相対的な傾向を見るだけに留まります。なお、スプリングの力f3は単純で、k(x-x0)です。
ワイヤー引き量とワイヤーを引く力f2、スプリングの力f3の関係(ただし各種摺動抵抗を無視)
へぇ～。手勘を裏付けるかのような穏やかなf2の上昇でした。
「でも、チェーンを押す力はどうなってるんだよ？」
そこは気になるところですが、難しいので考えていません。(昼休みにこのBlogを見ているシマノの開発の人がそっと教えてくれるに違いない！)
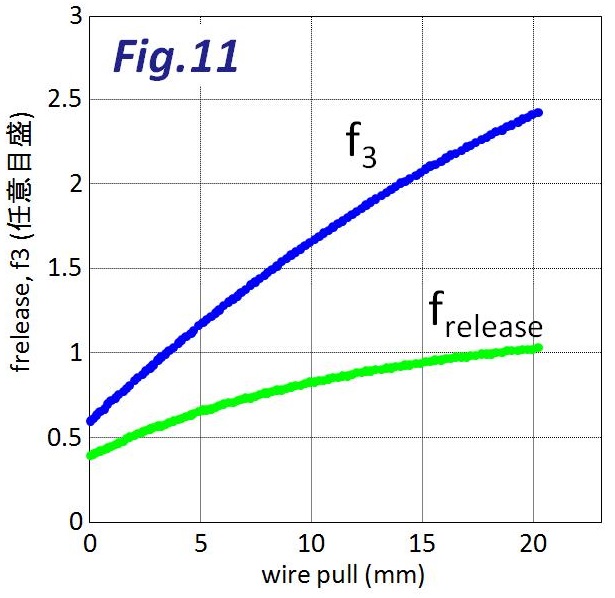
次は、ディレイラーが自力でトップ側に戻るときにガイドプーリーをトップ側に移動させる(というかチェーンを脱線させる)力「frelease」を算出します。P軸辺りを指で押してみると、これは明らかにトップ側の方が軽いのがわかります。式の導出経過は省略しますが、freleaseはこんな風になります。
ディレイラーが自力でトップ側に戻るときの力の式(ただし各種摺動抵抗を無視)
当然ですが、トップ側の戻し力はそれなりに弱くなります。グラフにするとこんな風。f3との相対比較でご覧ください。
ディレイラーが自力でトップ側に戻るときの力freleaseとワイヤー引っ張り力f3の位置関係(ただし各種摺動抵抗を無視)
以上、リアディレイラーにまつわる3つの力に関して、シマノの古い設計のRD-6500を題材として計算事例を示してみました。
ディレイラー設計者は、他にも多数存在するこういった数値関係を、隅から隅まで明瞭に理解しているんだろうなあ、と想像してしまいます。そして、実物の性能を理想に収斂させるための最適設計の方法論を日々、考えているに違いありません。
製品を創造するのは面白い
全くとりとめのない妄想にお付き合いいただき、ありがとうございます。
ここまでは、実際に存在する製品があるからこそできる検討(というか素人の邪推)です。見れば見るほど、先人の知恵と努力が語りかけてくるような気がするから不思議です。
製品開発というのは、何もないところからスタートすることもあり、机上計算～試作～テストの連続です。あとから考えれば当然のことも、開発途上では重要な気付き、発見だったりするわけです。
電動変速など、いわゆる変速機のメカトロ化も、こうすれば実現できる、と想像するのはそれほど難しくはないと思いますが、実際に製品化するためには、想像もしていなかったような様々な障壁を越える必要があります。
今、純メカ式、メカトロ式を問わず、ユーザーが手にしているその変速機には、開発者のアイデアとその実現に向けた惜しみない努力が反映されています。
開発に携わる方々は、当然のことながら、素人の妄想の遥かに先を行く絶妙なアイデアとハイブローな解析と、現場からのフィードバックを組み合わせて変速機の開発につなげているのだろうと思います。
メカトロや通信、ソフトウエア開発の要素も加わって、自転車の変速機の開発はますます面白くなってきているのではないでしょうか？
そうなんです。
最新の変速機の動きをよ～く見て考えるのは、アナタかも知れません！ アナタが使っているそのディレイラーをじっくり眺めて考えてみれば、開発者の意図を読み取ることができるかも知れません。
もしかしたら、新たな改良の方向性を提案したくなるかも知れません。そして、全く新しい変速機構を発明して世に問うのは、この妄想記事を最後まで読んで下さったアナタかも知れませんヨ！！
